二次函数y ax的平方+bx+a平方-2,(ab为常数答案解析
科目:czsx
来源:黄冈重点作业 初三数学(下)
题型:044
已知二次函数y=x2+bx+c(b,c为常数).
(1)若二次函数的图像经过A(-2,-3)和B(2,5)两点,求此二次函数的解析式;
(2)若(1)中的二次函数的图像过点P(m+1,n2+4n),且m≠n,求m+n的值.
查看答案和解析>>
科目:czsx
来源:
题型:
已知二次函数y=ax2-(a+1)x-4(a为常数)
(1)已知二次函数y=ax2-(a+1)x-4的图象的顶点在y轴上,求a的值;
(2)经探究发现无论a取何值,二次函数的图象一定经过平面直角坐标系内的两个定点.请求出这两个定点的坐标;
(3)已知关于x的一元二次方程ax2-(a+1)x-4=0的一个根在-1和0之间(不含-1和0),另一个根在2和3之间(不含2和3),试求整数a的值.
查看答案和解析>>
科目:czsx
来源:
题型:
(2012•西湖区一模)已知二次函数y=(x-3a)
2+a-1(a为常数),当a取不同的值时,其图象的顶点在一条直线上,这条直线的解析式是
.
查看答案和解析>>
科目:czsx
来源:
题型:
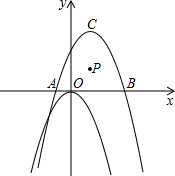
(2007•西城区二模)如图,在直角坐标系内有点P(1,1)、点C(1,3)和二次函数y=-x
2.
(1)若二次函数y=-x
2的图象经过平移后以C为顶点,请写出平移后的抛物线的解析式及一种平移的方法;
(2)若(1)中平移后的抛物线与x轴交于点A、点B(A点在B点的左侧),求cos∠PBO的值;
(3)在抛物线上是否存在一点D,使线段OC与PD互相平分?若存在,求出D点的坐标;若不存在,说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
如图,Rt△AOB是一张放在平面直角坐标系中的三角形纸片,点O与原点

重合,点A在x轴上,点B在y轴上
OB=,∠BAO=30°,将Rt△AOB折叠,使OB边落在AB边上,点O与点D重合,折痕为BE.
(1)求点E和点D的坐标;
(2)求经过O、D、A三点的二次函数解析式;
(3)设直线BE与(2)中二次函数图象的对称轴交于点F,M为OF中点,N为AF中点,在x轴上是否存在点P,使△PMN的周长最小,若存在,请求出点P的坐标和最小值;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
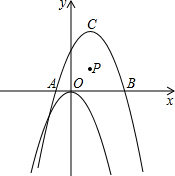 如图,在直角坐标系内有点P(1,1)、点C(1,3)和二次函数y=-x2.
如图,在直角坐标系内有点P(1,1)、点C(1,3)和二次函数y=-x2.
(1)若二次函数y=-x2的图象经过平移后以C为顶点,请写出平移后的抛物线的解析式及一种平移的方法;
(2)若(1)中平移后的抛物线与x轴交于点A、点B(A点在B点的左侧),求cos∠PBO的值;
(3)在抛物线上是否存在一点D,使线段OC与PD互相平分?若存在,求出D点的坐标;若不存在,说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
已知二次函数
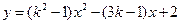
.
(1)二次函数的顶点在

轴上,求

的值;
(2)若二次函数与

轴的两个交点A、B均为整数点(坐标为整数的点),当

为整数时,求A、B两点的坐标.
查看答案和解析>>
科目:czsx
来源:2006年四川省眉山市青神县中考数学二模试卷(解析版)
题型:解答题
如图,Rt△AOB是一张放在平面直角坐标系中的三角形纸片,点O与原点重合,点A在x轴上,点B在y轴上

,∠BAO=30°,将Rt△AOB折叠,使OB边落在AB边上,点O与点D重合,折痕为BE.
(1)求点E和点D的坐标;
(2)求经过O、D、A三点的二次函数解析式;
(3)设直线BE与(2)中二次函数图象的对称轴交于点F,M为OF中点,N为AF中点,在x轴上是否存在点P,使△PMN的周长最小,若存在,请求出点P的坐标和最小值;若不存在,请说明理由.

查看答案和解析>>
科目:czsx
来源:2012年浙江省杭州市西湖区中考数学一模试卷(解析版)
题型:填空题
已知二次函数y=(x-3a)2+a-1(a为常数),当a取不同的值时,其图象的顶点在一条直线上,这条直线的解析式是 .
查看答案和解析>>
科目:czsx
来源:
题型:
已知二次函数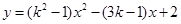 .
.
(1)二次函数的顶点在 轴上,求
轴上,求 的值;
的值;
(2)若二次函数与 轴的两个交点A、B均为整数点(坐标为整数的点),当
轴的两个交点A、B均为整数点(坐标为整数的点),当 为整数时,求A、B两点的坐标.
为整数时,求A、B两点的坐标.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
如图,Rt△AOB是一张放在平面直角坐标系中的三角形纸片,点O与原点 重合,点A在x轴上,点B在y轴上
重合,点A在x轴上,点B在y轴上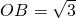 ,∠BAO=30°,将Rt△AOB折叠,使OB边落在AB边上,点O与点D重合,折痕为BE.
,∠BAO=30°,将Rt△AOB折叠,使OB边落在AB边上,点O与点D重合,折痕为BE.
(1)求点E和点D的坐标;
(2)求经过O、D、A三点的二次函数解析式;
(3)设直线BE与(2)中二次函数图象的对称轴交于点F,M为OF中点,N为AF中点,在x轴上是否存在点P,使△PMN的周长最小,若存在,请求出点P的坐标和最小值;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:2012年浙江省杭州市绿城育华中考数学模拟试卷(4月份)(解析版)
题型:填空题
已知二次函数y=(x-3a)2+a-1(a为常数),当a取不同的值时,其图象的顶点在一条直线上,这条直线的解析式是 .
查看答案和解析>>
科目:czsx
来源:2007年北京市西城区中考数学二模试卷(解析版)
题型:解答题
如图,在直角坐标系内有点P(1,1)、点C(1,3)和二次函数y=-x
2.
(1)若二次函数y=-x
2的图象经过平移后以C为顶点,请写出平移后的抛物线的解析式及一种平移的方法;
(2)若(1)中平移后的抛物线与x轴交于点A、点B(A点在B点的左侧),求cos∠PBO的值;
(3)在抛物线上是否存在一点D,使线段OC与PD互相平分?若存在,求出D点的坐标;若不存在,说明理由.

查看答案和解析>>
科目:czsx
来源:2010-2011学年北京市考数学一模试卷
题型:解答题
已知二次函数 .
.
(1)二次函数的顶点在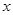 轴上,求
轴上,求 的值;
的值;
(2)若二次函数与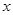 轴的两个交点A、B均为整数点(坐标为整数的点),当
轴的两个交点A、B均为整数点(坐标为整数的点),当 为整数时,求A、B两点的坐标.
为整数时,求A、B两点的坐标.
查看答案和解析>>
科目:czsx
来源:2010年中考数学考前10日信息题复习题精选(4)(解析版)
题型:解答题
(2006•青神县二模)如图,Rt△AOB是一张放在平面直角坐标系中的三角形纸片,点O与原点重合,点A在x轴上,点B在y轴上

,∠BAO=30°,将Rt△AOB折叠,使OB边落在AB边上,点O与点D重合,折痕为BE.
(1)求点E和点D的坐标;
(2)求经过O、D、A三点的二次函数解析式;
(3)设直线BE与(2)中二次函数图象的对称轴交于点F,M为OF中点,N为AF中点,在x轴上是否存在点P,使△PMN的周长最小,若存在,请求出点P的坐标和最小值;若不存在,请说明理由.

查看答案和解析>>
科目:czsx
来源:2010年江苏省扬州市高邮市九年级第二次网络阅卷适应性数学试卷(解析版)
题型:解答题
已知二次函数y=ax2-(a+1)x-4(a为常数)
(1)已知二次函数y=ax2-(a+1)x-4的图象的顶点在y轴上,求a的值;
(2)经探究发现无论a取何值,二次函数的图象一定经过平面直角坐标系内的两个定点.请求出这两个定点的坐标;
(3)已知关于x的一元二次方程ax2-(a+1)x-4=0的一个根在-1和0之间(不含-1和0),另一个根在2和3之间(不含2和3),试求整数a的值.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
已知二次函数y=ax2-(a+1)x-4(a为常数)
(1)已知二次函数y=ax2-(a+1)x-4的图象的顶点在y轴上,求a的值;
(2)经探究发现无论a取何值,二次函数的图象一定经过平面直角坐标系内的两个定点.请求出这两个定点的坐标;
(3)已知关于x的一元二次方程ax2-(a+1)x-4=0的一个根在-1和0之间(不含-1和0),另一个根在2和3之间(不含2和3),试求整数a的值.
查看答案和解析>>
科目:czsx
来源:辽宁省盘锦市第一完全中学2012届九年级第一次中考模拟数学试题
题型:022
若二次函数y=mx2-3x+2m-m2(m为常数)的图象经过原点,则m=________;
查看答案和解析>>
科目:czsx
来源:
题型:填空题
已知二次函数y=(x-3a)2+a-1(a为常数),当a取不同的值时,其图象的顶点在一条直线上,这条直线的解析式是________.
查看答案和解析>>
科目:czsx
来源:
题型:
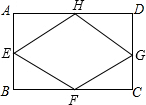
(2013•松北区一模)已知矩形ABCD的周长为12,E、F、G、H为矩形ABCD的各边中点,若AB=x,四边形EFGH的面积为y.
(1)请直接写出y与x的函数关系式;
(2)根据(1)中的函数关系式,计算当x为何值时,y最大,并求出最大值.
(参考公式:当x=-
时,二次函数y=ax+bx+c(a≠0)有最小(大)值
)
查看答案和解析>>

 (2007•西城区二模)如图,在直角坐标系内有点P(1,1)、点C(1,3)和二次函数y=-x2.
(2007•西城区二模)如图,在直角坐标系内有点P(1,1)、点C(1,3)和二次函数y=-x2. 重合,点A在x轴上,点B在y轴上OB=
重合,点A在x轴上,点B在y轴上OB=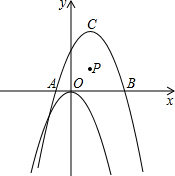 如图,在直角坐标系内有点P(1,1)、点C(1,3)和二次函数y=-x2.
如图,在直角坐标系内有点P(1,1)、点C(1,3)和二次函数y=-x2.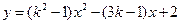 .
. 轴上,求
轴上,求 的值;
的值; 轴的两个交点A、B均为整数点(坐标为整数的点),当
轴的两个交点A、B均为整数点(坐标为整数的点),当 为整数时,求A、B两点的坐标.
为整数时,求A、B两点的坐标.  ,∠BAO=30°,将Rt△AOB折叠,使OB边落在AB边上,点O与点D重合,折痕为BE.
,∠BAO=30°,将Rt△AOB折叠,使OB边落在AB边上,点O与点D重合,折痕为BE.
![]() .
.![]() 轴上,求
轴上,求![]() 的值;
的值;![]() 轴的两个交点A、B均为整数点(坐标为整数的点),当
轴的两个交点A、B均为整数点(坐标为整数的点),当 为整数时,求A、B两点的坐标.
为整数时,求A、B两点的坐标. 重合,点A在x轴上,点B在y轴上
重合,点A在x轴上,点B在y轴上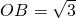 ,∠BAO=30°,将Rt△AOB折叠,使OB边落在AB边上,点O与点D重合,折痕为BE.
,∠BAO=30°,将Rt△AOB折叠,使OB边落在AB边上,点O与点D重合,折痕为BE.
 .
.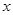 轴上,求
轴上,求 的值;
的值;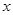 轴的两个交点A、B均为整数点(坐标为整数的点),当
轴的两个交点A、B均为整数点(坐标为整数的点),当 为整数时,求A、B两点的坐标.
为整数时,求A、B两点的坐标. ,∠BAO=30°,将Rt△AOB折叠,使OB边落在AB边上,点O与点D重合,折痕为BE.
,∠BAO=30°,将Rt△AOB折叠,使OB边落在AB边上,点O与点D重合,折痕为BE.
 (2013•松北区一模)已知矩形ABCD的周长为12,E、F、G、H为矩形ABCD的各边中点,若AB=x,四边形EFGH的面积为y.
(2013•松北区一模)已知矩形ABCD的周长为12,E、F、G、H为矩形ABCD的各边中点,若AB=x,四边形EFGH的面积为y.