已知在rt△abc中∠c=90,∠bac的角平分线答案解析
科目:czsx
来源:
题型:
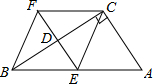
如图,已知在四边形ABFC中∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且CF=AE.
(1)试探究,四边形BECF是什么特殊的四边形并证明之;
(2)当∠A的大小满足什么条件时四边形BECF是正方形?并证明你的结论.
(3)若四边形BECF的面积是6(cm)
2且BC+AC=
cm时,求AB.
查看答案和解析>>
科目:czsx
来源:
题型:

如图,已知在四边形ABFC中∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且CF=AE.
(1)试探究,四边形BECF是什么特殊的四边形并证明之;
(2)若四边形BECF的面积是6cm
2且BC+AC=
cm时.求AB.
查看答案和解析>>
科目:czsx
来源:四川省期中题
题型:解答题
如图,已知在四边形ABFC中∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且CF=AE.
(1)试探究,四边形BECF是什么特殊的四边形并证明之;
(2)若四边形BECF的面积是6cm
2且BC+AC=

cm时.求AB.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
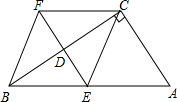 如图,已知在四边形ABFC中∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且CF=AE.
如图,已知在四边形ABFC中∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且CF=AE.
(1)试探究,四边形BECF是什么特殊的四边形并证明之;
(2)若四边形BECF的面积是6cm2且BC+AC= cm时.求AB.
cm时.求AB.
查看答案和解析>>
科目:czsx
来源:1课3练 单元达标测试八年级数学(下) 国标人教版
题型:044
如图,在Rt△ABC中,CF为直角的角平分线,FD⊥CA于D,FE⊥CB于E,则四边形CDFE是怎样的四边形?为什么?

查看答案和解析>>
科目:czsx
来源:
题型:

已知:如图中,AD是∠BAC的角平分线,DE∥AC,DF∥AB.
求证:四边形AEDF是菱形.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
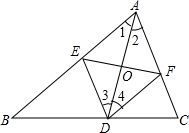 已知:如图中,AD是∠BAC的角平分线,DE∥AC,DF∥AB.
已知:如图中,AD是∠BAC的角平分线,DE∥AC,DF∥AB.
求证:四边形AEDF是菱形.
查看答案和解析>>
科目:czsx
来源:2012-2013学年青岛版九年级(上)第一次月考数学试卷(解析版)
题型:解答题
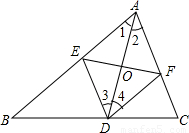
已知:如图中,AD是∠BAC的角平分线,DE∥AC,DF∥AB.
求证:四边形AEDF是菱形.
查看答案和解析>>
科目:czsx
来源:2013-2014学年广东东莞寮步宏伟中学九年级上学期第三次月考数学试卷(解析版)
题型:填空题
如图所示,已知在Rt△ABC中∠ACB=90°,AB=4,分别以AC,BC为直径作半圆,面积分别记为 ,
, ,则
,则 +
+ 的值等于__________.
的值等于__________.

查看答案和解析>>
科目:czsx
来源:2009年内蒙古包头市高中招生考试数学试卷
题型:013
已知在Rt△ABC中,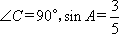 ,则tanB的值为
,则tanB的值为
[ ]
A.
B.
C.
D.
查看答案和解析>>
科目:czsx
来源:2006年宜州市中考第二次摸拟考试 数学试题
题型:013
查看答案和解析>>
科目:czsx
来源:同步题
题型:单选题
已知:在△ABC中,AD为∠BAC的角平分线上,DE⊥AB,F为AC上一点,且∠DFA=100。,则
A.DE>DF
B.DE<DF
C.DE=DF
D.不能确定DE、DF的大小
查看答案和解析>>
科目:czsx
来源:
题型:

如图,等边△ABC中,AD是∠BAC的角平分线,E为AD上一点,以BE为一边且在BE下方等边△BEF,连接CF.
(1)求证:AE=CF;
(2)求∠ACF的度数.
查看答案和解析>>
科目:czsx
来源:
题型:
如图1,已知AB=AC,D为∠BAC的角平分线上面一点,连接BD,CD;如图2,已知AB=AC,D、E为∠BAC的角平分线上面两点,连接BD,CD,BE,CE;如图3,已知AB=AC,D、E、F为∠BAC的角平分线上面三点,连接BD,CD,BE,CE,BF,CF;…,依次规律,第n个图形中有全等三角形的对数是( )
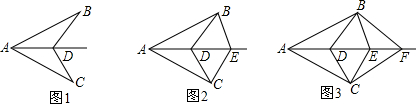
查看答案和解析>>
科目:czsx
来源:
题型:
在△ABC中,AD为∠BAC的角平分线,AE⊥BC,若∠B-∠C=40°,则∠DAE=
度.
查看答案和解析>>
科目:czsx
来源:
题型:
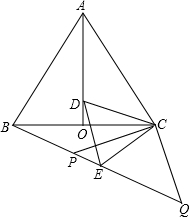
如图,等边△ABC中,AO是∠BAC的角平分线,D为AO上一点,以CD为一边且在CD下方作等边△CDE,连接BE.
(1)求证:△ACD≌△BCE;
(2)延长BE至Q,P为BQ上一点,连接CP、CQ使CP=CQ=5,若BC=8时,求PQ的长.
查看答案和解析>>
科目:czsx
来源:
题型:

23、如图,Rt△ABC,∠C=90°,∠CAB的角平分线AD交BC于点D,过点D作DE⊥AD,交AB于点E,以AE为直径作⊙O.求证:BC是⊙O的切线.
查看答案和解析>>
科目:czsx
来源:
题型:

如图,等边△ABC中,AD是∠BAC的角平分线,E为AD上一点,以BE为一边且在BE下方作等边△BEF,连接CF.
(1)求证:AE=CF;
(2)G为CF延长线上一点,连接BG.若BG=5,BC=8,求CG的长.
查看答案和解析>>
科目:czsx
来源:
题型:
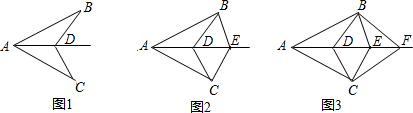
如图,已知AB=AC,D为∠BAC的角平分线上面一点,连接BD,CD;如图2,已知AB=AC,D、E为∠BAC的角平分线上面两点,连接BD,CD,BE,CE;如图3,已知AB=AC,D、E、F为∠BAC的角平分线上面三点,连接BD,CD,BE,CE,BF,CF;…,依次规律,第n个图形中有全等三角形的对数是
.
查看答案和解析>>
科目:czsx
来源:
题型:
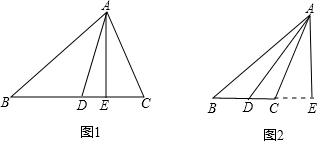
如图1,在△ABC中,AD是∠BAC的角平分线,AE是BC边上的高线,
(1)若∠ABC=40°∠ACB=80°,求∠DAE的度数;
(2)若∠ACB-∠ABC=m,试求∠DAE的度数(用含m的代数式表示);
(3)若△ABC是钝角三角形,如图2,∠ACB为钝角,(2)中条件不变,试问(2)中的结论还成立吗?请加以推理说明?
查看答案和解析>>

 如图,已知在四边形ABFC中∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且CF=AE.
如图,已知在四边形ABFC中∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且CF=AE. 如图,已知在四边形ABFC中∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且CF=AE.
如图,已知在四边形ABFC中∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且CF=AE. cm时.求AB.
cm时.求AB.
 如图,已知在四边形ABFC中∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且CF=AE.
如图,已知在四边形ABFC中∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且CF=AE. cm时.求AB.
cm时.求AB.

 ,
, ,则
,则 +
+ 的值等于__________.
的值等于__________.
 如图,等边△ABC中,AD是∠BAC的角平分线,E为AD上一点,以BE为一边且在BE下方等边△BEF,连接CF.
如图,等边△ABC中,AD是∠BAC的角平分线,E为AD上一点,以BE为一边且在BE下方等边△BEF,连接CF.
 如图,等边△ABC中,AO是∠BAC的角平分线,D为AO上一点,以CD为一边且在CD下方作等边△CDE,连接BE.
如图,等边△ABC中,AO是∠BAC的角平分线,D为AO上一点,以CD为一边且在CD下方作等边△CDE,连接BE. 23、如图,Rt△ABC,∠C=90°,∠CAB的角平分线AD交BC于点D,过点D作DE⊥AD,交AB于点E,以AE为直径作⊙O.求证:BC是⊙O的切线.
23、如图,Rt△ABC,∠C=90°,∠CAB的角平分线AD交BC于点D,过点D作DE⊥AD,交AB于点E,以AE为直径作⊙O.求证:BC是⊙O的切线. 如图,等边△ABC中,AD是∠BAC的角平分线,E为AD上一点,以BE为一边且在BE下方作等边△BEF,连接CF.
如图,等边△ABC中,AD是∠BAC的角平分线,E为AD上一点,以BE为一边且在BE下方作等边△BEF,连接CF.
