练习册

  • 练习册
  • 试题
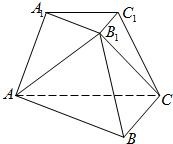    精英家教网 > 试题搜索列表 >PC⊥面ABC,DA∥PC，∠ACB=90°,E为PB的中,AC=AD=BC=1,PC=2设为上一点是确定的值使得二面角为

    PC⊥面ABC,DA∥PC，∠ACB=90°,E为PB的中,AC=AD=BC=1,PC=2设为上一点是确定的值使得二面角为答案解析

    科目：gzsx 来源： 题型：

    精英家教网如图，已知三棱台ABC-A1B1C1，等边三角形AB1C所在的平面与底面ABC垂直，且∠ACB=90°，设AC=2a，BC=a．
    （1）求点A到面B1BCC1的距离；
    （2）求二面角A-B1B-C的余弦值；
    （3）设
    AM
    =
    2
    5
    AB
    ，|MA1|=x，|CC1|=y，试将y表示为x的函数．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

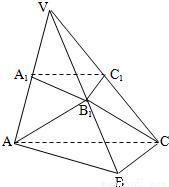
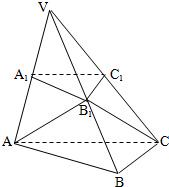    精英家教网如图，已知平面A1B1C1平行于三棱锥V-ABC的底面ABC，等边△AB1C所在的平面与底面ABC垂直，且∠ACB=90°，设AC=2a，BC=a
    （1）求证直线B1C1是异面直线AB1与A1C1的公垂线；
    （2）求点A到平面VBC的距离；
    （3）求二面角A-VB-C的大小．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    在三棱柱ABC—A′B′C′中，侧面CBB′C′⊥底面ABC,∠B′BC=60°,∠ACB=90°，且CB=CC′=CA.

    (1)求证：平面AB′C⊥平面A′C′B；

    (2)求异面直线A′B与AC′所成的角.

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    （06年山东卷理）（12分）

    如图，已知平面平行于三棱锥的底面ABC，等边△所在的平面与底面ABC垂直，且∠ACB=90°，设

    （1）求证直线是异面直线与的公垂线；

    （2）求点A到平面VBC的距离；

    （3）求二面角的大小。

    查看答案和解析>>

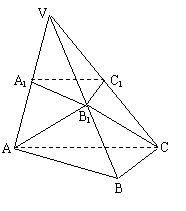
    科目：gzsx 来源：2010年广东省江门市高考数学后阶段备考指导和猜题试卷（解析版） 题型：解答题

    如图，已知三棱台ABC-A1B1C1，等边三角形AB1C所在的平面与底面ABC垂直，且∠ACB=90°，设AC=2a，BC=a．
    （1）求点A到面B1BCC1的距离；
    （2）求二面角A-B1B-C的余弦值；
    （3）设，|MA1|=x，|CC1|=y，试将y表示为x的函数．

    查看答案和解析>>

    科目：gzsx 来源：山东省高考真题 题型：解答题

    如图，已知平面A1B1C1平行于三棱锥V-ABC的底面ABC，等边△AB1C所在的平面与底面ABC垂直，且∠ACB=90°，设AC=2a，BC=a，
    （1）求证直线B1C1是异面直线AB1与A1C1的公垂线；
    （2）求点A到平面VBC的距离；
    （3）求二面角A-VB-C的大小。

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    如图，已知平面A1B1C1平行于三棱锥V-ABC的底面ABC，等边△ AB1C所在的平面与底面ABC垂直，且∠ACB=90°，设AC=2a,BC=a.

    （1）求证直线B1C1是异面直线AB1与A1C1的公垂线；

    （2）求点A到平面VBC的距离；

    （3）求二面角A-VB-C的大小.

    查看答案和解析>>

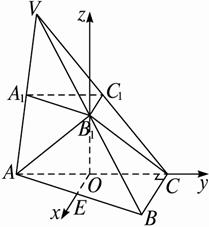
    科目：gzsx 来源： 题型：解答题

    如图，已知平面A1B1C1平行于三棱锥V-ABC的底面ABC，等边△AB1C所在的平面与底面ABC垂直，且∠ACB=90°，设AC=2a，BC=a
    （1）求证直线B1C1是异面直线AB1与A1C1的公垂线；
    （2）求点A到平面VBC的距离；
    （3）求二面角A-VB-C的大小．

    查看答案和解析>>

    科目：gzsx 来源：2006年山东省高考数学试卷（理科）（解析版） 题型：解答题

    如图，已知平面A1B1C1平行于三棱锥V-ABC的底面ABC，等边△AB1C所在的平面与底面ABC垂直，且∠ACB=90°，设AC=2a，BC=a
    （1）求证直线B1C1是异面直线AB1与A1C1的公垂线；
    （2）求点A到平面VBC的距离；
    （3）求二面角A-VB-C的大小．

    查看答案和解析>>

    科目：gzsx 来源： 题型：044

    如图，已知平面A1B1C1平行于三棱锥V?I>ABC的底面ABC，等边△AB1C所在的平面与底面ABC垂直，且∠ACB=90°,设AC=2a，BC=a.?

    (1)求证直线B1C1是异面直线AB1与A1C1的公垂线；?

    （2）求点A到平面VBC的距离；

    （3）求二面角A?I>VB?I>C的大小.?

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    如图，已知平面A1B1C1平行于三棱锥V—ABC的底面ABC，等边△AB1C所在的平面与底面ABC垂直，且∠ACB=90°.设AC=2a,BC=a.

    (Ⅰ)求证直线B1C1是异面直线AB1与A1C1的公垂线；

    (Ⅱ)求点A到平面VBC的距离；

    (Ⅲ)求二面角A—VB—C的大小.

    查看答案和解析>>

    科目：gzsx 来源：四川省绵阳南山中学2010届高三高考热身考试（理） 题型：解答题

     

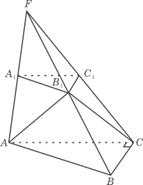
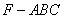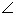    如图，已知平面平行于三棱锥的底面ABC，等边△所在平面与底面ABC垂直，且ACB=90°，设AC=2,BC=1.

    （Ⅰ）求点A到平面FBC的距离；

    （Ⅱ）求二面角A-FB-C的大小.                                 

     

     

                                                                              

     

     

     

     

     

     

    查看答案和解析>>

    科目：gzsx 来源：2011年高考数学综合复习试卷（1）（解析版） 题型：解答题

    如图，已知三棱台ABC-A1B1C1，等边三角形AB1C所在的平面与底面ABC垂直，且∠ACB=90°，设AC=2a，BC=a．
    （1）求点A到面B1BCC1的距离；
    （2）求二面角A-B1B-C的余弦值；
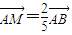    （3）设，|MA1|=x，|CC1|=y，试将y表示为x的函数．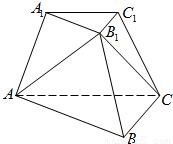

    查看答案和解析>>

    科目：gzsx 来源：2010年贵阳省贵阳六中高考数学模拟试卷（理科）（解析版） 题型：解答题

    如图，已知平面A1B1C1平行于三棱锥V-ABC的底面ABC，等边△AB1C所在的平面与底面ABC垂直，且∠ACB=90°，设AC=2a，BC=a
    （1）求证直线B1C1是异面直线AB1与A1C1的公垂线；
    （2）求点A到平面VBC的距离；
    （3）求二面角A-VB-C的大小．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    如图，已知平面A1B1C1平行于三棱锥V—ABC的底面ABC，等边△AB1C所在的平面与底面ABC垂直，且∠ACB=90°,设AC=2a，BC=a.

    (1)求证直线B1C1是异面直线AB1与A1C1的公垂线；

    （2）求点A到平面VBC的距离；

    （3）求二面角A—VB—C的大小.

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    如图，已知平面A1B1C1平行于三棱锥V-ABC的底面，等边三角形AB1C所在平面与面ABC垂直，且∠ACB=90°，设AC=2a，BC=a.

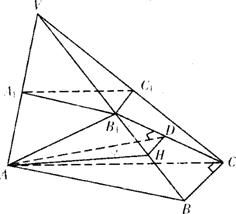
    (Ⅰ)证明：B1C1为异面直线AB1与A1C1的公垂线；

    (Ⅱ)求点A与平面VBC的距离；

    (Ⅲ)求二面角A-VB-C的大小.

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    （2013•和平区一模）如图，PC⊥平面ABC，DA∥PC，∠ACB=90°，E为PB的中点，AC=AD=BC=1，PC=2．
    （I）求证：DE∥平面ABC：
    （II）求证：PD⊥平面BCD；
    （III）设Q为PB上一点，
    PQ
    =λ
    PB
    ，试确定λ的值使得二面角Q-CD-B为45°．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    三棱锥P-ABC中，PA=PB=PC，∠ACB=90°，AC=CB=2．
    （Ⅰ）求证：平面PAB⊥平面ABC；
    （Ⅱ）若
    CB
    =2
    AD
    ，且异面直线PC与AD的夹角为60°时，求二面角P-CD-A的余弦值．

    查看答案和解析>>

    科目：gzsx 来源：2013年四川省成都市石室中学高考数学一模试卷（理科）（解析版） 题型：解答题

    三棱锥P-ABC中，PA=PB=PC，∠ACB=90°，AC=CB=2．
    （Ⅰ）求证：平面PAB⊥平面ABC；
    （Ⅱ）若，且异面直线PC与AD的夹角为60°时，求二面角P-CD-A的余弦值．

    查看答案和解析>>

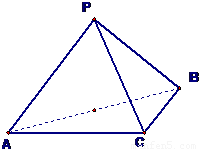
    科目：gzsx 来源：2013年天津市和平区高考数学一模试卷（理科）（解析版） 题型：解答题

    如图，PC⊥平面ABC，DA∥PC，∠ACB=90°，E为PB的中点，AC=AD=BC=1，PC=2．
    （I）求证：DE∥平面ABC：
    （II）求证：PD⊥平面BCD；
    （III）设Q为PB上一点，=λ，试确定λ的值使得二面角Q-CD-B为45°．

    查看答案和解析>>