
(06年山东卷理)(12分)
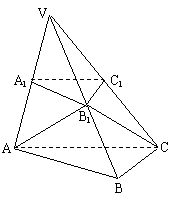
如图,已知平面![]() 平行于三棱锥
平行于三棱锥![]() 的底面ABC,等边△
的底面ABC,等边△![]() 所在的平面与底面ABC垂直,且∠ACB=90°,设
所在的平面与底面ABC垂直,且∠ACB=90°,设![]()
(1)求证直线![]() 是异面直线
是异面直线![]() 与
与![]() 的公垂线;
的公垂线;
(2)求点A到平面VBC的距离;
(3)求二面角![]() 的大小。
的大小。
解析:解法1:(Ⅰ)证明:∵平面![]()
![]() ∥平面
∥平面![]() ,
,
![]()
![]()
![]()
又∵平面![]() ⊥平面
⊥平面![]() ,平面
,平面![]() ∩平面
∩平面![]() ,
,
∴![]() ⊥平面
⊥平面![]() ,
,
![]()
![]() ,
,
又![]() ,
,![]() .
.
![]() 为
为![]() 与
与![]() 的公垂线.
的公垂线.
(Ⅱ)解法1:过A作![]() 于D,
于D,
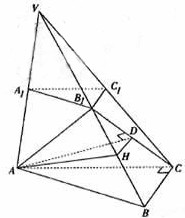
∵△![]() 为正三角形,∴D为
为正三角形,∴D为![]() 的中点.
的中点.
∵BC⊥平面![]() ,∴
,∴![]() ,
,
又![]() ,∴AD⊥平面
,∴AD⊥平面![]() ,
,
∴线段AD的长即为点A到平面![]() 的距离.
的距离.
在正△![]() 中,
中,![]() .
.
∴点A到平面![]() 的距离为
的距离为![]() .
.
解法2:取AC中点O连结![]() ,则
,则![]() ⊥平面
⊥平面![]() ,且
,且![]() =
=![]() .
.
由(Ⅰ)知![]() ,设A到平面
,设A到平面![]() 的距离为x,
的距离为x,
![]() ,
,
即![]() ,解得
,解得![]() .
.
即A到平面![]() 的距离为
的距离为![]() .
.
则![]()

![]()
所以,![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.
(III)过![]() 点作
点作![]() 于
于![]() ,连
,连![]() ,由三重线定理知
,由三重线定理知![]()
![]() 是二面角
是二面角![]() 的平面角。
的平面角。
在![]() 中,
中,![]()
![]()
![]() 。
。
![]() 。
。
所以,二面角![]() 的大小为arctan
的大小为arctan![]() .
.
解法二:
取![]() 中点
中点![]() 连
连![]() ,易知
,易知![]() 底面
底面![]() ,过
,过![]() 作直线
作直线![]() 交
交![]() 。
。
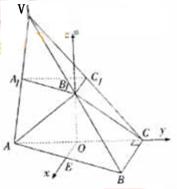
取![]() 为空间直角坐标系的原点,
为空间直角坐标系的原点,![]() 所在直线分别为
所在直线分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立如图所示的空间直角坐标系。
轴建立如图所示的空间直角坐标系。
则![]() 。
。
(I)![]() ,
,![]() ,
,
![]() ,
,
![]() 。
。![]()
又![]()
由已知![]() 。
。![]() ,
,
而![]() 。又
。又![]()
![]() 显然相交,
显然相交,
![]() 是
是![]() 的公垂线。
的公垂线。
(II)设平面![]() 的一个法向量
的一个法向量![]() ,
,
又![]()
由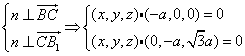
取![]() 得
得 ![]()
点![]() 到平面
到平面![]() 的距离,即
的距离,即![]() 在平面
在平面![]() 的法向量
的法向量![]() 上的投影的绝对值。
上的投影的绝对值。
![]() ,设所求距离为
,设所求距离为![]() 。
。
则![]()
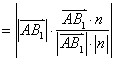
,![]() 所以,A到平面VBC的距离为
所以,A到平面VBC的距离为![]() .
.
(III)设平面![]() 的一个法向量
的一个法向量![]()
由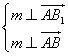
![]()
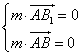
![]()
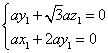
取![]()
![]()
![]()
![]() 二面角
二面角![]() 为锐角,
为锐角,
所以,二面角![]() 的大小为
的大小为![]()


 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源: 题型:
(06年山东卷理)如图,在等腰梯形ABCD中,AB=2DC=2,∠DAB=60°,E为AB的中点,将△ADE与△BEC分别沿ED、EC向上折起,使A、B重合于点P,则P-DCE三棱锥的外接球的体积为( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()

(12题图)
查看答案和解析>>
科目:高中数学 来源: 题型:
(06年山东卷理)如图,已知正三棱柱ABC-A1B1C1的所有棱长都相等,D是A1C1的 中点,则直线AD 与平面B1DC所成角的正弦值为 .
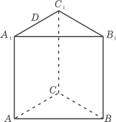
(15题图)
查看答案和解析>>
科目:高中数学 来源: 题型:
(06年山东卷理)下列四个命题中,真命题的序号有 (写出所有真命题的序号).
①将函数y=![]() 的图象按向量y=(-1,0)平移,得到的图象对应的函数表达式为y=
的图象按向量y=(-1,0)平移,得到的图象对应的函数表达式为y=![]()
②圆x2+y2+4x-2y+1=0与直线y=![]() 相交,所得弦长为2
相交,所得弦长为2
③若sin(![]() +
+![]() )=
)=![]() ,sin(
,sin(![]() -
-![]() )=
)=![]() ,则tan
,则tan![]() cot
cot![]() =5
=5
④如图,已知正方体ABCD- A1B1C1D1,P为底面ABCD内一动点,P到平面AA1D1D的距离与到直线CC1的距离相等,则P点的轨迹是抛物线的一部分.

(16题图)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com