求平面内到两定点AB的距离之比等于2的动点M的轨迹方程答案解析
科目:gzsx
来源:2010年河南省郑州市高二上学期第二月考数学理卷
题型:选择题
平面内到两定点 和
和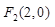 的距离之和为4的点M的轨迹是
( )
的距离之和为4的点M的轨迹是
( )
A.椭圆
B.线段
C.圆
D.以上都不对
查看答案和解析>>
科目:gzsx
来源:中学教材标准学案 数学 高二上册
题型:044
求平面内到一个定点F的距离等于到定直线l的距离的点的轨迹方程.

查看答案和解析>>
科目:gzsx
来源:2010年河南省郑州市外国语中学高二上学期第二月考数学理卷
题型:单选题
平面内到两定点 和
和 的距离之和为4的点M的轨迹是 ( )
的距离之和为4的点M的轨迹是 ( )
查看答案和解析>>
科目:gzsx
来源:
题型:
以下五个关于圆锥曲线的命题中:
①平面内到定点A(1,0)和定直线l:x=2的距离之比为
的点的轨迹方程是
+=1;
②点P是抛物线y
2=2x上的动点,点P在y轴上的射影是M点A的坐标是A(3,6),则|PA|+|PM|的最小值是6;
③平面内到两定点距离之比等于常数λ(λ>0)的点的轨迹是圆;
④若动点M(x,y)满足
=|2x-y-4|,则动点M的轨迹是双曲线;
⑤若过点C(1,1)的直线l交椭圆
+=1于不同的两点A,B,且C是AB的中点,则直线l的方程是3x+4y-7=0.
其中真命题的序号是
.(写出所有真命题的序号)
查看答案和解析>>
科目:gzsx
来源:
题型:
已知平面上有两定点
A、
B,|
AB|=2
A,平面上一动点
M到
A、
B两点距离之比为2∶1,求动点
M的轨迹方程.
查看答案和解析>>
科目:gzsx
来源:2010年江西省南昌市新建二中高考数学一模试卷(理科)(解析版)
题型:解答题
以下五个关于圆锥曲线的命题中:
①平面内到定点A(1,0)和定直线l:x=2的距离之比为

的点的轨迹方程是

;
②点P是抛物线y
2=2x上的动点,点P在y轴上的射影是M点A的坐标是A(3,6),则|PA|+|PM|的最小值是6;
③平面内到两定点距离之比等于常数λ(λ>0)的点的轨迹是圆;
④若动点M(x,y)满足

,则动点M的轨迹是双曲线;
⑤若过点C(1,1)的直线l交椭圆

于不同的两点A,B,且C是AB的中点,则直线l的方程是3x+4y-7=0.
其中真命题的序号是
.(写出所有真命题的序号)
查看答案和解析>>
科目:gzsx
来源:
题型:044
已知平面上有两定点A、B,|AB|=2A,平面上一动点M到A、B两点距离之比为2∶1,求动点M的轨迹方程.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知平面上有两定点A、B,|AB|=2a,平面上一动点M到A、B两点距离之比为2∶1,求动点M的轨迹方程.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知平面上有两定点
A、
B,|
AB|=
2a,平面上一动点
M到
A、
B两点距离之比为2∶1,求动点
M的轨迹方程.
查看答案和解析>>
科目:gzsx
来源:
题型:
(08年重点中学联考一理) 以下四个关于圆锥曲线的命题中:
①平面内到定点A(1,0)和定直线l:x=2的距离之比为 的点的轨迹方程是:
的点的轨迹方程是: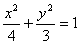
②点P是抛物线y2=2x上的动点,点P在y轴上的射影是M,点A的坐标是A(3,6),则
|PA|+|PM|的最小值是6;
③平面内到两定点距离之比等于常数λ(λ>0)的点的轨迹是圆;
④若过点C(1,1)的直线l交椭圆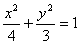 于不同的两点A、B,且C是AB的中点,则直线l的方程是3x+4y-7=0:
于不同的两点A、B,且C是AB的中点,则直线l的方程是3x+4y-7=0:
其中真命题的序号是 (写出所有真命题的序号)
查看答案和解析>>
科目:gzsx
来源:
题型:
以下命题:
①二直线平行的充要条件是它们的斜率相等;
②过圆上的点(x
0,y
0)与圆x
2+y
2=r
2相切的直线方程是
x0x+y0y=r2;
③平面内到两定点的距离之和等于常数的点的轨迹是椭圆;
④抛物线上任意一点M到焦点的距离都等于点M到其准线的距离.
其中正确命题的标号是
②④
②④
.
查看答案和解析>>
科目:gzsx
来源:
题型:
以下四个关于圆锥曲线的命题中:
①设A、B为两个定点,k为非零常数,
||-||=k,则动点P的轨迹为双曲线;
②平面内到两定点距离之和等于常数的点的轨迹是椭圆
③若方程
+=1表示焦点在x轴上的椭圆,则1<t<
④双曲线
-=1与椭圆+y2=1有相同的焦点.
其中真命题的序号为
③、④
③、④
(写出所有真命题的序号)
查看答案和解析>>
科目:gzsx
来源:
题型:
平面内到两定点的距离之比为1:2的动点的轨迹是( )
查看答案和解析>>
科目:gzsx
来源:
题型:
已知平面上有两定点
A、
B,|AB|
=2
a,平面上一动点
M到
A、
B两点距离之比为2∶1,则动点
M的轨迹方程为________________.
查看答案和解析>>
科目:gzsx
来源:
题型:
“平面内到两定点F
1、F
2的距离之和为定值的点的轨迹是椭圆(大前提).平面内动点M到两定点F
1(-2,0)、F
2(2,0)的距离之和为4(小前提),则M点的轨迹是椭圆(结论)中错误的是__________.
查看答案和解析>>
科目:gzsx
来源:
题型:
“平面内到两定点F
1、F
2的距离之和为定值的点的轨迹是椭圆(大前提).平面内动点M到两定点F
1(-2,0)、F
2(2,0)的距离之和为4(小前提),则M点的轨迹是椭圆(结论)中错误的是__________.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知平面上有两定点A、B,|AB|=2a,平面上一动点M到A、B两点距离之比为2∶1,则动点M的轨迹方程为________________.
查看答案和解析>>

 和
和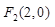 的距离之和为4的点M的轨迹是
( )
的距离之和为4的点M的轨迹是
( ) 和
和 的距离之和为4的点M的轨迹是 ( )
的距离之和为4的点M的轨迹是 ( ) 的点的轨迹方程是
的点的轨迹方程是 ;
; ,则动点M的轨迹是双曲线;
,则动点M的轨迹是双曲线; 于不同的两点A,B,且C是AB的中点,则直线l的方程是3x+4y-7=0.
于不同的两点A,B,且C是AB的中点,则直线l的方程是3x+4y-7=0.![]() 的点的轨迹方程是:
的点的轨迹方程是:![]()
![]() 于不同的两点A、B,且C是AB的中点,则直线l的方程是3x+4y-7=0:
于不同的两点A、B,且C是AB的中点,则直线l的方程是3x+4y-7=0: