
科目:czsx 来源: 题型:
科目:czsx 来源: 题型:解答题
科目:czsx 来源:2011年广东省茂名市高州市“缅茄杯”学科竞赛试卷(初三数学)(解析版) 题型:解答题
科目:czsx 来源:广东省竞赛题 题型:解答题
科目:czsx 来源: 题型:单选题
| x | … | -1 | 0 | 1 | 3 | … |
| y | … | -3 | 1 | 3 | 1 | … |
科目:czsx 来源: 题型:单选题
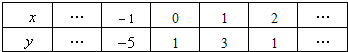
科目:czsx 来源: 题型:单选题
| x | … | -1 | 0 | 1 | 3 | … |
| y | … | -3 | 1 | 3 | 1 | … |
科目:czsx 来源: 题型:
| A、抛物线的开口向上,与y轴交于正半轴 | B、抛物线的开口向上,与y轴交于负半轴 | C、抛物线的开口向下,与y轴交于正半轴 | D、抛物线的开口向下,与y轴交于负半轴 |
科目:czsx 来源:不详 题型:单选题
| A.抛物线的开口向上,与y轴交于正半轴 |
| B.抛物线的开口向上,与y轴交于负半轴 |
| C.抛物线的开口向下,与y轴交于正半轴 |
| D.抛物线的开口向下,与y轴交于负半轴 |
科目:czsx 来源:2007-2008学年山东省烟台市莱州市九年级(上)期中数学试卷(解析版) 题型:选择题
科目:czsx 来源:山东省期中题 题型:单选题
科目:czsx 来源: 题型:单选题
科目:czsx 来源:2011年滨海新区大港初中毕业生学业考试第一次模拟试卷数学 题型:解答题
(本小题10分)在平面直角坐标系中,将直线l: 沿x轴翻折,得到一条新直线与x轴交于点A,与y轴交于点B,将抛物线
沿x轴翻折,得到一条新直线与x轴交于点A,与y轴交于点B,将抛物线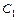 :
: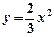 沿x轴平移,得到一条新抛物线
沿x轴平移,得到一条新抛物线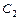 与y轴交于点D,与直线AB交于点E、点F.
与y轴交于点D,与直线AB交于点E、点F.
(Ⅰ)求直线AB的解析式;
(Ⅱ)若线段DF∥x轴,求抛物线 的解析式;
的解析式;
(Ⅲ)在(2)的条件下,若点F在y轴右侧,过F作FH⊥x轴于点G,与直线l交于点H,一条直线m(m不过△AFH的顶点)与AF交于点M,与FH交于点N,如果直线m既垂直于直线AB又平分△AFH的面积,求直线m的解析式.
科目:czsx 来源:2011年初中毕业升学考试(湖北十堰卷)数学 题型:解答题
(本小题10分)
在平面直角坐标系中,将直线l: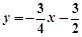 沿x轴翻折,得到一条新直线与x轴交于点A,与y轴交于点B,将抛物线
沿x轴翻折,得到一条新直线与x轴交于点A,与y轴交于点B,将抛物线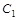 :
: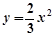 沿x轴平移,得到一条新抛物线
沿x轴平移,得到一条新抛物线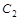 与y轴交于点D,与直线AB交于点E、点F.
与y轴交于点D,与直线AB交于点E、点F.
(Ⅰ)求直线AB的解析式;
(Ⅱ)若线段DF∥x轴,求抛物线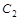 的解析式;
的解析式;
(Ⅲ)在(2)的条件下,若点F在y轴右侧,过F作FH⊥x轴于点G,与直线l交于点H,一条直线m(m不过△AFH的顶点)与AF交于点M,与FH交于点N,如果直线m既垂直于直线AB又平分△AFH的面积,求直线m的解析式.
科目:czsx 来源: 题型:
(本小题10分)在平面直角坐标系中,将直线l: 沿x轴翻折,得到一条新直线与x轴交于点A,与y轴交于点B,将抛物线
沿x轴翻折,得到一条新直线与x轴交于点A,与y轴交于点B,将抛物线:
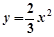 沿x轴平移,得到一条新抛物线
沿x轴平移,得到一条新抛物线与y轴交于点D,与直线AB交于点E、点F.
(Ⅰ)求直线AB的解析式;
(Ⅱ)若线段DF∥x轴,求抛物线的解析式;
(Ⅲ)在(2)的条件下,若点F在y轴右侧,过F作FH⊥x轴于点G,与直线l交于点H,一条直线m(m不过△AFH的顶点)与AF交于点M,与FH交于点N,如果直线m既垂直于直线AB又平分△AFH的面积,求直线m的解析式.
科目:czsx 来源:2009年北京市朝阳区中考数学一模试卷(解析版) 题型:解答题
科目:czsx 来源: 题型:
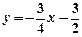 沿x轴翻折,得到一条新直线与x轴交于点A,与y轴交于点B,将抛物线
沿x轴翻折,得到一条新直线与x轴交于点A,与y轴交于点B,将抛物线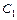 :
: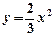 沿x轴平移,得到一条新抛物线
沿x轴平移,得到一条新抛物线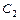 与y轴交于点D,与直线AB交于点E、点F.
与y轴交于点D,与直线AB交于点E、点F. 的解析式;
的解析式;
科目:czsx 来源:2010年浙江省名校中考数学模拟试卷(二)(解析版) 题型:解答题
科目:czsx 来源: 题型:
科目:czsx 来源: 题型:
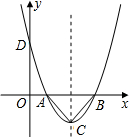 一开口向上的抛物线与x轴交于A(m-2,0),B(m+2,0)两点,记抛物线顶点为C,且AC⊥BC.
一开口向上的抛物线与x轴交于A(m-2,0),B(m+2,0)两点,记抛物线顶点为C,且AC⊥BC.