科目：gzsx 来源：2009-2010学年度新课标高三上学期数学单元测试7-理科-不等式 题型：解答题
（09数学理全国1第22题） （12分）
设函数
在两个极值点
，且
（1）求
满足的约束条件，并在下面的坐标平面内，画出满足这些条件的点
的区域；
（2）证明：
科目：gzsx 来源： 题型：
如图，坐标纸上的每个单元格的边长为1，由下往上的
六个点：1，2，3，4，5，6的横纵坐标分别对应数列
的前12项，如下表所示：
|
等于 ▲ 。 科目：gzsx 来源： 题型：
（07年安徽卷）（本小题满分14分）
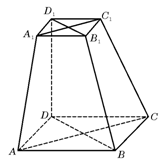
如图,在六面体
中,四边形ABCD是边
长为2的正方形,四边形
是边长为1的正方
形,
平面,平面ABCD,
求证: (Ⅰ)
与
共面，
与
共面．
(Ⅱ)求证:平面
(Ⅲ)求二面角
的大小(用反三角函数值表示).
第(17)题图
科目：gzsx 来源： 题型：
（03年全国卷理）（12分，附加题4 分）
（I）设
是集合
且
}中所有的数从小到大排列成的数列，即
，
，
，
，
，
，…
将数列各项按照上小下大，左小右大的原则写成如下的三角形数表：
3
5 6
9 10 12
― ― ― ―
…………
⑴写出这个三角形数表的第四行、第五行各数；
⑵求
（II）（本小题为附加题，如果解答正确，加4 分，但全卷总分不超过150分）
设
是集合
，且
中所有的数从小到大排列成的数列，已知
，求
.
科目：gzsx 来源： 题型：
（07年安徽卷）（本小题满分14分）
如图,在六面体
中,四边形ABCD是边
长为2的正方形,四边形
是边长为1的正方
形,
平面,平面ABCD,
求证: (Ⅰ)
与
共面，
与
共面．
(Ⅱ)求证:平面
(Ⅲ)求二面角
的大小(用反三角函数值表示).
第(17)题图
科目：gzsx 来源： 题型：044
在全国高中数学联赛第二卷中只有三道题，已知
(1)某校25个学生参加竞赛，每个学生至少解出一道题；(2)在所有没有解出第一题的学生中，解出第二道题的人数是解出第三题的人数多2倍；(3)只解出第一题的学生比余下的学生中解出第一题的人数多1；(4)只解出一道题的学生中，有一半没有解出第一题，问共有多少学生只解出第二题？科目：gzsx 来源：数学教研室 题型：044
在全国高中数学联赛第二卷中只有三道题，已知(1)某校25个学生参加竞赛，每个学生至少解出一道题；(2)在所有没有解出第一题的学生中，解出第二道题的人数是解出第三题的人数多2倍；(3)只解出第一题的学生比余下的学生中解出第一题的人数多1；(4)只解出一道题的学生中，有一半没有解出第一题，问共有多少学生只解出第二题？
科目：gzsx 来源： 题型：
| 参考数据 | 当Χ2≤2.706时，无充分证据判定变量A，B有关联，可以认为两变量无关联； |
| 当Χ2＞2.706时，有90%把握判定变量A，B有关联； | |
| 当Χ2＞3.841时，有95%把握判定变量A，B有关联； | |
| 当Χ2＞6.635时，有99%把握判定变量A，B有关联． |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
科目：gzsx 来源： 题型：
（全国卷Ⅱ文）（本小题满分12分）
|
|
（Ⅰ）求a,b的值；
（Ⅱ）C上是否存在点P，使得当l绕F转到某一位置时，有 成立？
若存在，求出所有的P的坐标与l的方程；若不存在，说明理由。
的内角
所对的边长分别为
，且
．
的值；
的最大值．
的内角
所对的边长分别为
，且
．
的值；
的最大值．
中，
，
． 
的值；
，求
中，
，
． 
的值；
，求
的长．
中，
，
． 
的值；
，求
的长．
中，
，
． 
的值；
，求
的侧面
是菱形，
平面
；
是
上的点，且
平面
，求
的值.
注意：解答请写在答题卷上17题对应位置
的侧面
是菱形，
平面
；
是
上的点，且
平面
，求
的值.
注意：解答请写在答题卷上17题对应位置
的内角
所对的边长分别为
，且
，
．
；
，求
．
的内角
所对的边长分别为
，且
，
．
；
，求
．
中，
，
．
．证明：数列
是等差数列；
项和
．