
科目:gzsx 来源: 题型:
| AB |
| n |
| n |
| AC |
| n |
| BC |
| A、-2 | B、2 | C、0 | D、2或-2 |
科目:gzsx 来源:2011年人教A版模块考试数学试卷1(必修4)(解析版) 题型:选择题
 ,
, ,且
,且 •
• ,则
,则 •
•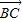 等于( )
等于( )科目:gzsx 来源:不详 题型:单选题
| AB |
| n |
| n |
| AC |
| n |
| BC |
| A.-2 | B.2 | C.0 | D.2或-2 |
科目:gzsx 来源:2009-2010学年山东省日照市实验高中高一(下)期末数学练习试卷7(必修3、4)(解析版) 题型:选择题
 ,
, ,且
,且 •
•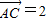 ,则
,则 •
•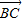 等于( )
等于( )科目:gzsx 来源:2011-2012学年广东省肇庆市南丰中学高三(上)数学复习试卷C (必修4)(解析版) 题型:选择题
 ,
, ,且
,且 •
• ,则
,则 •
• 等于( )
等于( )科目:gzsx 来源:广东省广州市培正中学2010-2011学年高一下学期期中考试数学试题 题型:013
已知A,B,C为平面上不共线的三点,若向量![]() =(1,1),
=(1,1),![]() =(1,-1),且
=(1,-1),且![]() ·
·![]() =2,则
=2,则![]() ·
·![]() 等于
等于
-2
2
0
2或-2
科目:gzsx 来源:2010年高三数学综合检测试卷2(必修4)(解析版) 题型:选择题
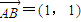 ,
, ,且
,且 •
• ,则
,则 •
• 等于( )
等于( )科目:gzsx 来源: 题型:
已知A,B,C为平面上不共线的三点,若向量![]() =(1,1),n=(1,-1),且n·
=(1,1),n=(1,-1),且n·![]() =2,则n·
=2,则n·![]() 等于( )
等于( )
(A)-2 (B)2 (C)0 (D)2或-2
科目:gzsx 来源: 题型:
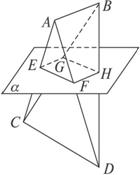
(1)求证:四边形EFHG是一个平行四边形;
(2)若AB=CD=a,试求四边形EFGH的周长.
科目:gzsx 来源: 题型:047
如图,已知A、B、C、D四点不共面,且AB∥平面α,CD∥α,AC∩α=E,AD∩α=F,BD∩α=H,BC∩α=G.

求证:EFHG是一个平行四边形.
科目:gzsx 来源:数学教研室 题型:047
如图,已知A、B、C、D四点不共面,且AB∥平面α,CD∥α,AC∩α=E,AD∩α=F,BD∩α=H,BC∩α=G.

求证:EFHG是一个平行四边形.
科目:gzsx 来源:数学教研室 题型:047
如图所示,已知A、B、C、D四点不共面,且AB∥平面α,CD∥平面α,AC∩α=E,AD∩α=F,BD∩α=H,BC∩α=G.
求证:EFHG是一个平行四边形.

科目:gzsx 来源: 题型:047
如图所示,已知
A、B、C、D四点不共面,且AB∥平面α,CD∥平面α,AC∩α=E,AD∩α=F,BD∩α=H,BC∩α=G.求证:
EFHG是一个平行四边形.
科目:gzsx 来源:“伴你学”新课程 数学·选修1-2(人教B版) 人教B版 题型:047
已知A、B、C、D四点不共面,M、N分别是△ABD和△BCD的重心,求证:MN∥平面ACD.