科目：gzsx 来源：2015届山东省高一10月月考数学试卷（解析版） 题型：解答题
已知函数f(x)是定义在（0，+∞）上的单调增函数，满足f(xy)=f(x)+f(y),f(3)=1
（1）求f(1)的值
（2）若满足f(x) +f(x-8)≤2 求x的取值范围
科目：gzsx 来源： 题型：
（07年陕西卷理）f(x)是定义在（0，±∞）上的非负可导函数，且满足xf(x)+f(x)≤0,对任意正数a、b,若a＜b，则必有
A.af(b) ≤bf(a) B.bf(a) ≤af(b)
C.af(a) ≤f(b) D.bf(b) ≤f(a)
科目：gzsx 来源：2007年普通高等学校招生全国统一考试理科数学卷（陕西） 题型：选择题
f(x)是定义在（0，±∞）上的非负可导函数，且满足xf(x)+f(x)≤0,对任意正数a、b,若 a＜b，则必有
A.af(b) ≤bf(a) B.bf(a) ≤af(b)
C.af(a) ≤f(b) D.bf(b) ≤f(a)
科目：gzsx 来源： 题型：
（08年龙岩一中模拟理）f(x)是定义在（0，±∞）上的非负可导函数，且满足xf(x)+f(x)≤0,对任意正数a、b,若a＜b，则必有（ ）
A．af(b) ≤bf(a) B．bf(a) ≤af(b)
C．af(a) ≤f(b) D．bf(b) ≤f(a)
科目：gzsx 来源：重庆市2008届六校高中三年级第一次联合模拟考试数学理科 题型：044
已知函数f(x)是定义在区间[0，＋∞)上的增函数，当a＞0且a≠1时，解关于x的不等式：f(loga(3x2－2x))＜f(loga(12x＋24))
科目：gzsx 来源：重庆市2008届六校高中三年级第一次联合模拟考试数学文科 题型：044
已知函数f(x)是定义在区间[0，＋∞)上的增函数，当a＞0且a≠1时，解关于x的不等式：f(loga(3x2－2x))＜f(loga(12x＋24))
科目：gzsx 来源：广东省期末题 题型：解答题
。 
。 科目：gzsx 来源： 题型：
对任意的［0,1］上的单峰函数f(x),下面研究缩短其含峰区间长度的方法.
(1)证明对任意的x1、x2∈(0,1),x1＜x2,若f(x1)≥f(x2),则(0,x2)为含峰区间;若f(x1)≤f(x2),则(x1,1)为含峰区间;
(2)对给定的r(0＜r＜0.5),证明存在x1、x2∈(0,1),满足x2-x1≥2r,使得由(1)所确定的含峰区间的长度不大于0.5+r;
(3)选取x1、x2∈(0,1),x1＜x2,由(1)可确定含峰区间为(0,x2)或(x1,1),在所得的含峰区间内选取x3,由x3与x1或x3与x2类似地可确定一个新的含峰区间.在第一次确定的含峰区间为(0,x2)的情况下,试确定x1、x2、x3的值,满足两两之差的绝对值不小于0.02,且使得新的含峰区间的长度缩短到0.34.
(区间长度等于区间的右端点与左端点之差)
科目：gzsx 来源：数学教研室 题型：044
科目：gzsx 来源： 题型：044
已知f(x)是定义在（0，+∞）上的单调递增函数，且对定义域内任意x，y都有f(x·y)=f(x)+f(y)且f(2)=1，求使不等式f(x)+f(x－3)≤2成立的x的取值范围。
科目：gzsx 来源：河南省沁阳一中2010届高三第四次月考、理科数学试卷 题型：044
已知函数f(x)是定义在区间[0，＋∞)上的增函数，当a＞0且a≠1时，解关于x的不等式：f(loga(3x2－2x))＜f(loga(12x＋24))
科目：gzsx 来源：0103 期中题 题型：单选题
[ ]
) 
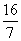) 科目：gzsx 来源： 题型：
.f(x)是定义在（0，±∞）上的非负可导函数，且满足xf(x)+f(x)≤0,对任意正数a、b,若a＜b，则必有
A. af(b) ≤bf(a) B. bf(a) ≤af(b)
C. af(a) ≤f(b) D. bf(b) ≤f(a)
科目：gzsx 来源：2013届海南省高二下学期期末考试文科数学试卷（解析版） 题型：解答题
已知函数y=f(x)是定义在区间［-
，］上的偶函数，且
x∈［0，］时，
（1）求函数f(x)的解析式；
（2）若矩形ABCD的顶点A，B在函数y=f(x)的图像上，顶点C，D在x轴上，求矩形ABCD面积的最大值.
科目：gzsx 来源： 题型：
已知奇函数f(x)是定义在(－3，3)上的减函数，且满足不等式f(x－3)+f(x2－3)<0,设不等式解集为A，B=A∪{x|1≤x≤
},求函数g(x)=－3x2+3x－4(x∈B)的最大值。
科目：gzsx 来源： 题型：
①定义域为［-b,b］;②是奇函数;③最小值为0;④在定义域内单调递增.
其中正确说法的个数有
A.4 B.3 C.2 D.1
科目：gzsx 来源：2011-2012学年江苏省第二学期期中文科数学试卷（解析版） 题型：解答题
已知函数f(x)=
是定义在(－1，1)上的奇函数，且f(
)=
.
(1)试确定函数f(x)的解析式；(2)用定义证明f(x)在(－1，1)上是增函数；(3)解不等式f(t－1)+f(t)<0.
)·lgx+1，求f(x)的解析式及值域.