
科目:czsx 来源:2010届浙江省温岭市九年级上学期期末考试数学试卷(解析版) 题型:选择题
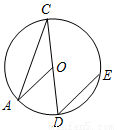
如图, 已知CD为⊙O的直径,过点D的弦DE平行于半径OA,若∠CDE的度数是40o,则∠C的度数是 ( )
A.50o B. 40o C. 30o D.20o
科目:czsx 来源:不详 题型:单选题
| A.50o | B.40o | C.30o | D.20o |

科目:czsx 来源: 题型:
如图, 已知CD为⊙O的直径,过点D的弦DE平行于半径OA,若∠D的度数是50o,则∠C的度数是( )
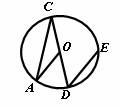
A.50o B. 40o C. 30o D.25o
科目:czsx 来源:2010届浙江省温岭市九年级上学期期末考试数学试卷(带解析) 题型:单选题
如图, 已知CD为⊙O的直径,过点D的弦DE平行于半径OA,若∠CDE的度数是40o,则∠C的度数是 ( )
| A.50o | B.40o | C.30o | D.20o |

科目:czsx 来源: 题型:
科目:czsx 来源: 题型:
科目:czsx 来源: 题型:
 两线段相等或不相等的关系除外)(不要求证明).
两线段相等或不相等的关系除外)(不要求证明). 科目:czsx 来源: 题型:
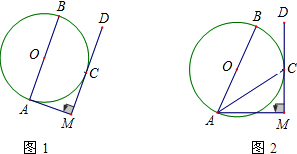 ⊙O的切线CD,过A作CD的垂线,垂足是M点.
⊙O的切线CD,过A作CD的垂线,垂足是M点.科目:czsx 来源: 题型:

科目:czsx 来源: 题型:
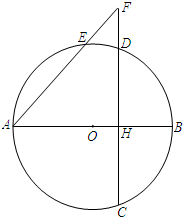
 如图已知在⊙O中,直径AB=10,点E是OA上任意一点,过E作弦CD⊥AB,点F是弧BC上一点,连接AF交CE于H,连接AC、CF、BF.
如图已知在⊙O中,直径AB=10,点E是OA上任意一点,过E作弦CD⊥AB,点F是弧BC上一点,连接AF交CE于H,连接AC、CF、BF.科目:czsx 来源:2013年广东省广州市高级中等学校招生考试数学 题型:044
已知AB是⊙O的直径,AB=4,点C在线段AB的延长线上运动,点D在⊙O上运动(不与点B重合),连接CD,且CD=OA.
(1)当OC=![]() 时(如图),求证:CD是⊙O的切线;
时(如图),求证:CD是⊙O的切线;

(2)当OC>![]() 时,CD所在直线于⊙O相交,设另一交点为E,连接AE.
时,CD所在直线于⊙O相交,设另一交点为E,连接AE.
①当D为CE中点时,求△ACE的周长;
②连接OD,是否存在四边形AODE为梯形?若存在,请说明梯形个数并求此时AE·ED的值;若不存在,请说明理由.
科目:czsx 来源:2010年天津市初中毕业生学业考试数学试卷 题型:047
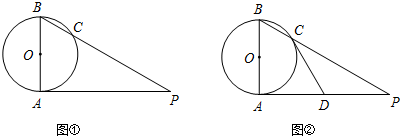
已知AB是⊙O的直径,AP是⊙O的切线,A是切点,BP与⊙O交于点C.
(Ⅰ)如图,若AB=2,∠P=30°,求AP的长(结果保留根号);

(Ⅱ)如图,若D为AP的中点,求证直线CD是⊙O的切线.

科目:czsx 来源: 题型:解答题
 已知AB是⊙O的直径,弦CD⊥AB,垂足为H,AH=5,CD=
已知AB是⊙O的直径,弦CD⊥AB,垂足为H,AH=5,CD=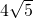 ,点E在⊙O上,射线AE与射线CD相交于点F,设AE=x,DF=y.
,点E在⊙O上,射线AE与射线CD相交于点F,设AE=x,DF=y. ,求DF的长.
,求DF的长.科目:czsx 来源: 题型:
已知AB是⊙O的直径,弦CD⊥AB,垂足为H,AH=5,CD=![]() ,点E在⊙O上,射线AE与射线CD相交于点F,设AE=
,点E在⊙O上,射线AE与射线CD相交于点F,设AE=![]() ,DF=
,DF=![]() .
.
(1) ![]() 求⊙O的半径;
求⊙O的半径;
(2) 如图,当点E在AD上时,求![]() 与
与![]() 之间的函
之间的函
数解析式,并写出函数的定义域;
(3)  如果EF=
如果EF=![]() ,求DF的长.
,求DF的长.
科目:czsx 来源: 题型:
已知AB是⊙O的直径,弦CD⊥AB,垂足为H,AH=5,CD=![]() ,点E在⊙O上,射线AE与射线CD相交于点F,设AE=x,DF=y.
,点E在⊙O上,射线AE与射线CD相交于点F,设AE=x,DF=y.
(1)求⊙O的半径;
(2)如图,当点E在AD上时,求y与x之间的函数解析式,并写出函数的定义域;
(3)如果EF=![]() ,求DF的长.
,求DF的长.

科目:czsx 来源:2013届内蒙古海拉尔区第四中学九年级上学期期末考试数学试卷(带解析) 题型:解答题
已知AB是⊙O的直径,AP是⊙O的切线,A是切点,BP与⊙O交于点C.
(1)如图①,若AB=2,∠P=30°,求AP的长(结果保留根号);
(2)如图②,若D为AP的中点,求证直线CD是⊙O的切线.
科目:czsx 来源:2013届浙江建德李家镇初级中学九年级上期末综合数学试卷(二)(带解析) 题型:解答题
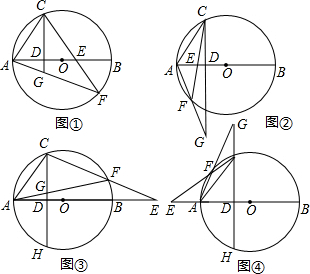
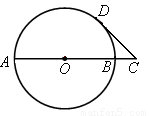
已知AB是⊙O的直径,弦CD⊥AB于点G,E是直线AB上一动点(不与点A、B、G重合),直线DE交⊙O于点F,直线CF交直线AB于点P.设⊙O的半径为R.
(1)如图1,当点E在直径AB上时,试证明:OE·OP=R2.(提示:作直径FQ交⊙O于Q,并连结DQ)
(2)当点E在AB(或BA)的延长线上时,以如图2点E的位置为例,请你画出符合题意的图形,标注上字母,(1)中的结论是否成立?请说明理由.
科目:czsx 来源:2013年上海市静安区中考数学二模试卷(解析版) 题型:解答题
 ,点E在⊙O上,射线AE与射线CD相交于点F,设AE=x,DF=y.
,点E在⊙O上,射线AE与射线CD相交于点F,设AE=x,DF=y. ,求DF的长.
,求DF的长.
科目:czsx 来源:2013年初中毕业升学考试(广东广州卷)数学(解析版) 题型:解答题
已知AB是⊙O的直径,AB=4,点C在线段AB的延长线上运动,点D在⊙O 上运动(不与点B重合),连接CD,且CD=OA.
(1)当OC=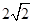 时(如图),求证:CD是⊙O的切线;
时(如图),求证:CD是⊙O的切线;
(2)当OC>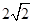 时,CD所在直线于⊙O相交,设另一交点为E,连接AE.
时,CD所在直线于⊙O相交,设另一交点为E,连接AE.
①当D为CE中点时,求△ACE的周长;
②连接OD,是否存在四边形AODE为梯形?若存在,请说明梯形个数并求此时AE·ED的值;若不存在,请说明理由。