如图在四边形abcd中.ef分别在边ad,bc上.且ae等于cf答案解析
科目:czsx
来源:
题型:044
如图,E、F分别是平行四边形ABCD的边BA、DC延长线上的点,且AE=CF,EF交AD于G,交BC于H。
(1)图中的全等三角形有 对,它们分别是 ;(不添加任何辅助线)
(2)请在(1)问中选出一对你认为全等的三角形进行证明。
我选择的是: 。
证明:

查看答案和解析>>
科目:czsx
来源:四川省中考真题
题型:解答题
如图,E、F分别是平行四边形ABCD的边BA、DC延长线上的点,且AE=CF,EF交AD于G,交BC于H。
(1)图中的全等三角形有______对,它们分别是______;(不添加任何辅助线)
(2)请在(1)问中选出一对你认为全等的三角形进行证明,我选择的是:_____。
查看答案和解析>>
科目:czsx
来源:
题型:
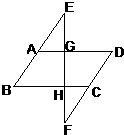
21、如图,E、F分别是平行四边形ABCD的边BA、DC延长线上的点,且AE=CF,EF交AD于G,交BC于H.
(1)图中的全等三角形有
2
对,它们分别是
△AEG≌△CFH和△BEH≌△DFG
;(不添加任何辅助线)
(2)请在(1)问中选出一对你认为全等的三角形进行证明.我选择的是:
△AEG≌△CFH
.
查看答案和解析>>
科目:czsx
来源:2006年四川省乐山市中考数学试卷(课标卷)(解析版)
题型:解答题
(2006•乐山)如图,E、F分别是平行四边形ABCD的边BA、DC延长线上的点,且AE=CF,EF交AD于G,交BC于H.
(1)图中的全等三角形有______对,它们分别是______;(不添加任何辅助线)
(2)请在(1)问中选出一对你认为全等的三角形进行证明.我选择的是:______.

查看答案和解析>>
科目:czsx
来源:
题型:
张老师给爱好学习的小军和小俊提出这样一个问题:如图1,在△ABC中,AB=AC,点P为边BC上的任一点,过点P作PD⊥AB,PE⊥AC,垂足分别为D、E,过点C作CF⊥AB,垂足为F.求证:PD+PE=CF.
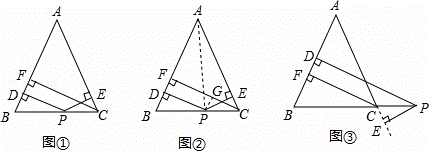
小军的证明思路是:如图2,连接AP,由△ABP与△ACP面积之和等于△ABC的面积可以证得:PD+PE=CF.
小俊的证明思路是:如图2,过点P作PG⊥CF,垂足为G,可以证得:PD=GF,PE=CG,则PD+PE=CF.
【变式探究】如图3,当点P在BC延长线上时,其余条件不变,求证:PD﹣PE=CF;
请运用上述解答中所积累的经验和方法完成下列两题:
【结论运用】如图4,将矩形ABCD沿EF折叠,使点D落在点B上,点C落在点C′处,点P为折痕EF上的任一点,过点P作PG⊥BE、PH⊥BC,垂足分别为G、H,若AD=8,CF=3,求PG+PH的值;
【迁移拓展】图5是一个航模的截面示意图.在四边形ABCD中,E为AB边上的一点,ED⊥AD,EC⊥CB,垂足分别为D、C,且AD•CE=DE•BC,AB=2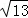 dm,AD=3dm,BD=
dm,AD=3dm,BD= dm.M、N分别为AE、BE的中点,连接DM、CN,求△DEM与△CEN的周长之和.
dm.M、N分别为AE、BE的中点,连接DM、CN,求△DEM与△CEN的周长之和.



查看答案和解析>>
科目:czsx
来源:
题型:
【问题情境】张老师给爱好学习的小军和小俊提出这样一个问题:如图1,在△ABC中,AB=AC,点P为边BC上的任一点,过点P作PD⊥AB,PE⊥AC,垂足分别为D、E,过点C作CF⊥AB,垂足为F.求证:PD+PE=CF.

小军的证明思路是:如图2,连接AP,由△ABP与△ACP面积之和等于△ABC的面积可以证得:PD+PE=CF.
小俊的证明思路是:如图2,过点P作PG⊥CF,垂足为G,可以证得:PD=GF,PE=CG,则PD+PE=CF.
【变式探究】如图3,当点P在BC延长线上时,其余条件不变,求证:PD-PE=CF;
请运用上述解答中所积累的经验和方法完成下列两题:
【结论运用】如图4,将矩形ABCD沿EF折叠,使点D落在点B上,点C落在点C′处,点P为折痕EF上的任一点,过点P作PG⊥BE、PH⊥BC,垂足分别为G、H,若AD=8,CF=3,求PG+PH的值;
【迁移拓展】图5是一个航模的截面示意图.在四边形ABCD中,E为AB边上的一点,ED⊥AD,EC⊥CB,垂足分别为D、C,且AD•CE=DE•BC,AB=2
dm,AD=3dm,BD=
dm.M、N分别为AE、BE的中点,连接DM、CN,求△DEM与△CEN的周长之和.

查看答案和解析>>
科目:czsx
来源:
题型:解答题
11.【问题情境】张老师给爱好学习的小军和小俊提出这样一个问题:如图1,在△ABC中,AB=AC,点P为边BC上的任一点,过点P作PD⊥AB,PE⊥AC,垂足分别为D、E,过点C作CF⊥AB,垂足为F.求证:PD+PE=CF.

小军的证明思路是:如图2,连接AP,由△ABP与△ACP面积之和等于△ABC的面积可以证得:PD+PE=CF.
小俊的证明思路是:如图2,过点P作PG⊥CF,垂足为G,可以证得:PD=GF,PE=CG,则PD+PE=CF.
【变式探究】如图3,当点P在BC延长线上时,其余条件不变,求证:PD-PE=CF;
请运用上述解答中所积累的经验和方法完成下列两题:
【结论运用】如图4,将矩形ABCD沿EF折叠,使点D落在点B上,点C落在点C′处,点P为折痕EF上的任一点,过点P作PG⊥BE、PH⊥BC,垂足分别为G、H,若AD=8,CF=3,求PG+PH的值;
【迁移拓展】图5是一个航模的截面示意图.在四边形ABCD中,E为AB边上的一点,ED⊥AD,EC⊥CB,垂足分别为D、C,且AD•CE=DE•BC,AB=2$\sqrt{13}$dm,AD=3dm,BD=$\sqrt{37}$dm.M、N分别为AE、BE的中点,连接DM、CN,求△DEM与△CEN的周长之和.

查看答案和解析>>
科目:czsx
来源:
题型:解答题
10.【问题情境】
张老师给爱好学习的小军和小俊提出这样的一个问题:如图1,在△ABC中,AB=AC,点P为边BC上任一点,过点P作PD⊥AB,PE⊥AC,垂足分别为D,E,过点C作CF⊥AB,垂足为F,求证:PD+PE=CF.

小军的证明思路是:如图2,连接AP,由△ABP与△ACP面积之和等于△ABC的面积可以证得:PD+PE=CF.
小俊的证明思路是:如图2,过点P作PG⊥CF,垂足为G,可以证得:PD=GF,PE=CG,则PD+PE=CF.
【变式探究】
如图3,当点P在BC延长线上时,其余条件不变,求证:PD-PE=CF;
请运用上述解答中所积累的经验和方法完成下列两题:
【结论运用】
如图4,将矩形ABCD沿EF折叠,使点D落在点B上,点C落在点C′处,点P为折痕EF上的任一点,过点P作PG⊥BE、PH⊥BC,垂足分别为G、H,若AD=8,CF=3,求PG+PH的值;
【迁移拓展】
图5是一个航模的截面示意图.在四边形ABCD中,E为AB边上的一点,ED⊥AD,EC⊥CB,垂足分别为D、C,且AD•CE=DE•BC,AB=2$\sqrt{13}$dm,AD=3dm,BD=$\sqrt{37}$dm.M、N分别为AE、BE的中点,连接DM、CN,求△DEM与△CEN的周长之和.
查看答案和解析>>



 21、如图,E、F分别是平行四边形ABCD的边BA、DC延长线上的点,且AE=CF,EF交AD于G,交BC于H.
21、如图,E、F分别是平行四边形ABCD的边BA、DC延长线上的点,且AE=CF,EF交AD于G,交BC于H.

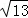 dm,AD=3dm,BD=
dm,AD=3dm,BD= dm.M、N分别为AE、BE的中点,连接DM、CN,求△DEM与△CEN的周长之和.
dm.M、N分别为AE、BE的中点,连接DM、CN,求△DEM与△CEN的周长之和.






