科目：czsx 来源： 题型：解答题
科目：czsx 来源： 题型：解答题
科目：czsx 来源：2014-2015学年江苏省八年级下学期第三次月考数学卷（解析版） 题型：解答题
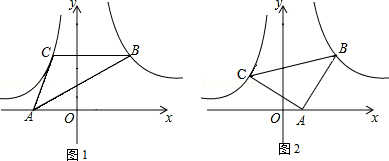
（本题12分）如图，点B（2，2）在双曲线
（x＞0）上，点C在双曲线
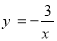（x＜0）上，点A是x轴上一动点，连接BC、AC、AB．
（1）求k的值；
（2）如图1，当BC∥x轴时，△ABC的面积；
（3）如图2，当点A运动到x轴正半轴时，若△ABC是等腰直角三角形，∠BAC=90°，求点A的坐标．
科目：czsx 来源： 题型：
科目：czsx 来源： 题型：
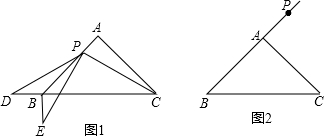
在等腰直角三角形ABC中，∠BAC=90°，AB=AC，直线MN过点A且MN∥BC.以点B为一锐角顶点作Rt△BDE，∠BDE=90°，且点D在直线MN上（不与点A重合）.如图1，DE与AC交于点P，易证：BD=DP.(无需写证明过程)
（1）在图2中，DE与CA延长线交于点P，BD=DP是否成立？如果成立，请给予
证明，如果不成立，请说明理由；
（2）在图3中，DE与AC延长线交于点P，BD与DP是否相等？请直接写出你的结论，无需证明.
科目：czsx 来源：2014-2015学年山西省晋中市平遥县九年级下学期4月中考模拟数学试卷（解析版） 题型：解答题
在等腰直角三角形ABC中，∠BAC=90°，AB=AC，直线MN过点A且MN∥BC，过点B为一锐角顶点作Rt△BDE，∠BDE=90°，且点D在直线MN上（不与点A重合），如图1，DE与AC交于点P，易证：BD=DP．（无需写证明过程）
（1）在图2中，DE与CA延长线交于点P，BD=DP是否成立？如果成立，请给予证明；如果不成立，请说明理由；
（2）在图3中，DE与AC延长线交于点P，BD与DP是否相等？请直接写出你的结论，无需证明．
科目：czsx 来源：2013届上海市金山区九年级上学期期末考试数学试卷（带解析） 题型：填空题
已知在等腰直角三角形ABC中，∠BAC＝90°，AB＝AC＝4，将边AB绕着点A旋转至
位置，且与AC边之间的夹角为30°，那么线段
的长等于_______。
科目：czsx 来源：2012-2013学年上海市金山区九年级上学期期末考试数学试卷（解析版） 题型：填空题
已知在等腰直角三角形ABC中，∠BAC＝90°，AB＝AC＝4，将边AB绕着点A旋转至
位置，且与AC边之间的夹角为30°，那么线段
的长等于_______。
科目：czsx 来源：不详 题型：填空题
位置，且与AC边之间的夹角为30°，那么线段
的长等于_______。科目：czsx 来源：2013年辽宁省营口市中考模拟（一）数学试卷（带解析） 题型：解答题
如图，△ABC和△DEF是两个全等的等腰直角三角形，∠BAC=∠EDF=90°，△DEF的顶点E与△ABC的斜边BC的中点重合．将△DEF绕点E旋转，旋转过程中，线段DE与线段AB相交于点P，线段EF与射线CA相交于点Q．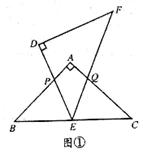
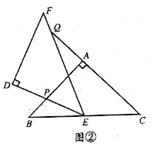
（1）如图①，当点Q在线段AC上，且AP=AQ时，求证：△BPE≌△CQE；
（2）如图②，当点Q在线段CA的延长线上时，求证：△BPE∽△CEQ；并求当BP=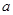
，CQ=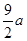
时，P、Q两点间的距离 (用含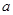的代数式表示)．
科目：czsx 来源：2012年初中毕业升学考试（四川成都卷）数学（带解析） 题型：解答题
如图，△ABC和△DEF是两个全等的等腰直角三角形，∠BAC=∠EDF=90°，△DEF的顶点E与△ABC的斜边BC的中点重合．将△DEF绕点E旋转，旋转过程中，线段DE与线段AB相交于点P，线段EF与射线CA相交于点Q．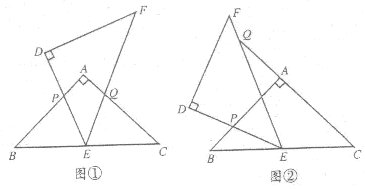
（1）如图①，当点Q在线段AC上，且AP=AQ时，求证：△BPE≌△CQE；
（2）如图②，当点Q在线段CA的延长线上时，求证：△BPE∽△CEQ；并求当BP=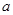
，CQ=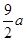
时，P、Q两点间的距离 (用含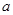的代数式表示)．
科目：czsx 来源：2013届北京市三十一中学初三上学期期中考试数学试卷（带解析） 题型：解答题
如图，△ABC和△DEF是两个全等的等腰直角三角形，∠BAC=∠EDF=90°，△DEF的顶点E与△ABC的斜边BC的中点重合．将△DEF绕点E旋转，旋转过程中，线段DE与线段AB相交于点P，线段EF与射线CA相交于点Q．
（1）如图①，当点Q在线段AC上，且AP=AQ时，求证：△BPE≌△CQE；
（2）如图②，当点Q在线段CA的延长线上时，求证：△BPE∽△CEQ；并求当BP=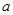
，CQ=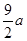
时，P、Q两点间的距离 (用含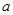的代数式表示)．
科目：czsx 来源：2013年初中数学单元提优测试卷-相似的判定解答题（带解析） 题型：解答题
如图，△ABC和△DEF是两个全等的等腰直角三角形，∠BAC=∠EDF=90°，△DEF的顶点E与△ABC的斜边BC的中点重合．将△DEF绕点E旋转，旋转过程中，线段DE与线段AB相交于点P，线段EF与射线CA相交于点Q．
（1）如图①，当点Q在线段AC上，且AP=AQ时，求证：△BPE≌△CQE；
（2）如图②，当点Q在线段CA的延长线上时，求证：△BPE∽△CEQ；并求当BP=a，CQ=
时，P、Q两点间的距离（用含a的代数式表示）．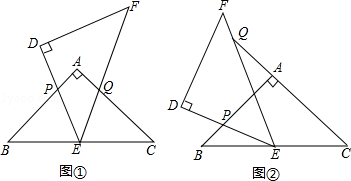
科目：czsx 来源：2013年辽宁省营口市中考模拟（一）数学试卷（解析版） 题型：解答题
如图，△ABC和△DEF是两个全等的等腰直角三角形，∠BAC=∠EDF=90°，△DEF的顶点E与△ABC的斜边BC的中点重合．将△DEF绕点E旋转，旋转过程中，线段DE与线段AB相交于点P，线段EF与射线CA相交于点Q．
（1）如图①，当点Q在线段AC上，且AP=AQ时，求证：△BPE≌△CQE；
（2）如图②，当点Q在线段CA的延长线上时，求证：△BPE∽△CEQ；并求当BP=
，CQ=
时，P、Q两点间的距离 (用含的代数式表示)．
科目：czsx 来源：2013年初中数学单元提优测试卷-相似的判定解答题（解析版） 题型：解答题
如图，△ABC和△DEF是两个全等的等腰直角三角形，∠BAC=∠EDF=90°，△DEF的顶点E与△ABC的斜边BC的中点重合．将△DEF绕点E旋转，旋转过程中，线段DE与线段AB相交于点P，线段EF与射线CA相交于点Q．
（1）如图①，当点Q在线段AC上，且AP=AQ时，求证：△BPE≌△CQE；
（2）如图②，当点Q在线段CA的延长线上时，求证：△BPE∽△CEQ；并求当BP=a，CQ=
时，P、Q两点间的距离（用含a的代数式表示）．
科目：czsx 来源：2012-2013学年北京市初三上学期期中考试数学试卷（解析版） 题型：解答题
如图，△ABC和△DEF是两个全等的等腰直角三角形，∠BAC=∠EDF=90°，△DEF的顶点E与△ABC的斜边BC的中点重合．将△DEF绕点E旋转，旋转过程中，线段DE与线段AB相交于点P，线段EF与射线CA相交于点Q．
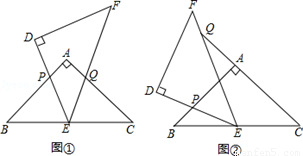
（1）如图①，当点Q在线段AC上，且AP=AQ时，求证：△BPE≌△CQE；
（2）如图②，当点Q在线段CA的延长线上时，求证：△BPE∽△CEQ；并求当BP=
，CQ=
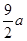时，P、Q两点间的距离 (用含的代数式表示)．
科目：czsx 来源：2012年初中毕业升学考试（四川成都卷）数学（解析版） 题型：解答题
如图，△ABC和△DEF是两个全等的等腰直角三角形，∠BAC=∠EDF=90°，△DEF的顶点E与△ABC的斜边BC的中点重合．将△DEF绕点E旋转，旋转过程中，线段DE与线段AB相交于点P，线段EF与射线CA相交于点Q．
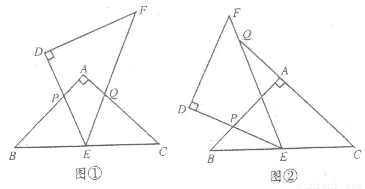
（1）如图①，当点Q在线段AC上，且AP=AQ时，求证：△BPE≌△CQE；
（2）如图②，当点Q在线段CA的延长线上时，求证：△BPE∽△CEQ；并求当BP=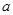
，CQ=
时，P、Q两点间的距离 (用含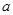的代数式表示)．
科目：czsx 来源：四川省中考真题 题型：解答题
，CQ=
时，P、Q两点间的距离 (用含
的代数式表示)．
科目：czsx 来源： 题型：
如图，△ABC和△DEF是两个全等的等腰直角三角形，∠BAC=∠EDF=90°，△DEF的顶点E与△ABC的斜边BC的中点重合．将△DEF绕点E旋转，旋转过程中，线段DE与线段AB相交于点P，线段EF与射线CA相交于点Q．
（1）如图①，当点Q在线段AC上，且AP=AQ时，求证：△BPE≌△CQE；
（2）如图②，当点Q在线段CA的延长线上时，求证：△BPE∽△CEQ；并求当BP=
，CQ=
时，P、Q两点间的距离 (用含的代数式表示)．新 课 标 第一网
科目：czsx 来源： 题型：
如图，△ABC和△DEF是两个全等的等腰直角三角形，∠BAC=∠EDF=90°，△DEF的顶点E与△ABC的斜边BC的中点重合．将△DEF绕点E旋转，旋转过程中，线段DE与线段AB相交于点P，线段EF与射线CA相交于点Q．
（1）如图①，当点Q在线段AC上，且AP=AQ时，求证：△BPE≌△CQE；
（2）如图②，当点Q在线段CA的延长线上时，求证：△BPE∽△CEQ；并求当BP=
，CQ=
时，P、Q两点间的距离 (用含的代数式表示)．
 |