
科目:czsx 来源: 题型:
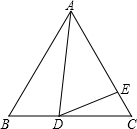 已知:如图,等边△ABC中,AB=1.若D、E分别是BC、AC上的点(点D与B、C不重合),且∠ADE=60°.设BD=x,AE=y.
已知:如图,等边△ABC中,AB=1.若D、E分别是BC、AC上的点(点D与B、C不重合),且∠ADE=60°.设BD=x,AE=y.科目:czsx 来源: 题型:
科目:czsx 来源: 题型:解答题
科目:czsx 来源:2010-2011学年福建省泉州市洛江区九年级(上)期末数学试卷(解析版) 题型:解答题

科目:czsx 来源: 题型:
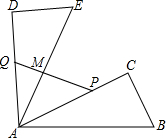 使点B落在点E处,点C落在点D处.P、Q分别为线段AC、AD上的两个动点,且AQ=2PC,连接PQ交线段AE于点M.
使点B落在点E处,点C落在点D处.P、Q分别为线段AC、AD上的两个动点,且AQ=2PC,连接PQ交线段AE于点M.科目:czsx 来源: 题型:解答题
 使点B落在点E处,点C落在点D处.P、Q分别为线段AC、AD上的两个动点,且AQ=2PC,连接PQ交线段AE于点M.
使点B落在点E处,点C落在点D处.P、Q分别为线段AC、AD上的两个动点,且AQ=2PC,连接PQ交线段AE于点M.科目:czsx 来源:2010年上海市奉贤区中考数学三模试卷(解析版) 题型:解答题

科目:czsx 来源: 题型:
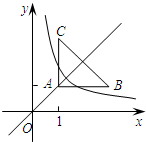 如图:等腰直角三角形ABC位于第一象限,AB=AC=2,直角顶点A在直线y=x上,其中A点的横坐标为1,且两条直角边AB、AC分别平行于x轴、y轴,若双曲线y=
如图:等腰直角三角形ABC位于第一象限,AB=AC=2,直角顶点A在直线y=x上,其中A点的横坐标为1,且两条直角边AB、AC分别平行于x轴、y轴,若双曲线y=| k |
| x |
| A、1<k<2 |
| B、1≤k≤3 |
| C、1≤k≤4 |
| D、1≤k<4 |
科目:czsx 来源: 题型:
 F=AE,连接AF、BE和CF.
F=AE,连接AF、BE和CF.科目:czsx 来源: 题型:
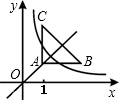 如图,等腰直角三角形ABC位于第一象限,AB=AC=2,直角顶点A在直线y=x上,其中A点的横坐标为1,且两条直角边AB、AC分别平行于x轴、y轴,若双曲线y=
如图,等腰直角三角形ABC位于第一象限,AB=AC=2,直角顶点A在直线y=x上,其中A点的横坐标为1,且两条直角边AB、AC分别平行于x轴、y轴,若双曲线y=| k | x |
科目:czsx 来源:2008年山西省初中毕业升学统一考试、数学试题及答案 题型:044
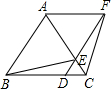
如图,已知△ABC是等边三角形,D、E分别在边BC、AC上,且CD=CE,连结DE并延长至点F,使EF=AE,连结AF、BE和CF.
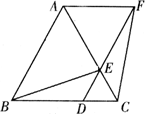
(1)请在图中找出一对全等三角形,用符号“≌”表示,并加以证明.
(2)判断四边形ABDF是怎样的四边形,并说明理由.
(3)若AB=6,BD=2DC,求四边形ABEF的面积.
科目:czsx 来源:2012-2013学年江苏省无锡市前洲中学八年级3月月考数学试卷 题型:单选题
如图:等腰直角三角形ABC位于第一象限,AB=AC=2,直角顶点A在直线y=x上,其中A点的横坐标为1,且两条直角边AB、AC分别平行于x轴、y轴,若双曲线 (k≠0)与
(k≠0)与 有交点,则k的取值范围是( )
有交点,则k的取值范围是( )
A. B.
B. C.
C.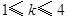 D.
D.
科目:czsx 来源:2013年初中数学单元提优测试卷-点的坐标与待定系数法求函数(带解析) 题型:单选题
如图:等腰直角三角形ABC位于第一象限,AB=AC=2,直角顶点A在直线y=x上,其中A点的横坐标为1,且两条直角边AB、AC分别平行于x轴、y轴,若双曲线y= (k≠0)与△ABC有交点,则k的取值范围是( )
(k≠0)与△ABC有交点,则k的取值范围是( )
A.1<k<2 B.1≤k≤3 C.1≤k≤4 D.1≤k<4
科目:czsx 来源:2014届江苏省无锡市八年级3月月考数学试卷 题型:选择题
如图:等腰直角三角形ABC位于第一象限,AB=AC=2,直角顶点A在直线y=x上,其中A点的横坐标为1,且两条直角边AB、AC分别平行于x轴、y轴,若双曲线 (k≠0)与
(k≠0)与 有交点,则k的取值范围是( )
有交点,则k的取值范围是( )

A.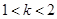 B.
B.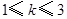 C.
C.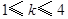 D.
D.
科目:czsx 来源:2014届江苏省无锡市八年级3月月考数学试卷 题型:选择题
如图:等腰直角三角形ABC位于第一象限,AB=AC=2,直角顶点A在直线y=x上,其中A点的横坐标为1,且两条直角边AB、AC分别平行于x轴、y轴,若双曲线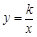 (k≠0)与
(k≠0)与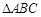 有交点,则k的取值范围是( )
有交点,则k的取值范围是( )

A. B.
B.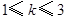 C.
C.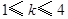 D.
D.
科目:czsx 来源:2013年初中数学单元提优测试卷-点的坐标与待定系数法求函数(解析版) 题型:选择题
如图:等腰直角三角形ABC位于第一象限,AB=AC=2,直角顶点A在直线y=x上,其中A点的横坐标为1,且两条直角边AB、AC分别平行于x轴、y轴,若双曲线y=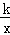 (k≠0)与△ABC有交点,则k的取值范围是( )
(k≠0)与△ABC有交点,则k的取值范围是( )
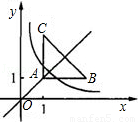
A.1<k<2 B.1≤k≤3 C.1≤k≤4 D.1≤k<4
科目:czsx 来源:2013届河南西华县东王营中学八年级下期中考试数学试卷(解析版) 题型:选择题
如图,等腰直角三角形ABC位于第一象限,AB=AC=2,直角顶点A在直线Y=x上,其中A点的横坐标为1,且两条直角边AB、AC分别平行于X轴、Y轴,若双曲线y= 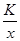 (K≠0)与△ABC有交点,则K的取值范围是( )
(K≠0)与△ABC有交点,则K的取值范围是( )
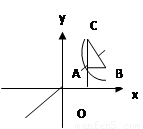
A.1〈K〈2 B.1≤K≤2 C.1〈K〈4 D. 1≤K≤4
科目:czsx 来源:2011-2012年浙江省义蓬片九年级第一学期第一阶段考试数学卷 题型:选择题
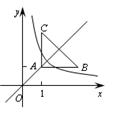
如图:等腰直角三角形ABC位于第一象限,AB=AC=2,直角顶点A在直线y=x上,其中A点的横坐标为1,且两条直角边AB、AC分别平行于x轴、y轴,若双曲线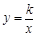 (k≠0)与
(k≠0)与 有交点,则k的取值范围是( )
有交点,则k的取值范围是( )
A.1<k<2 B.1≤k≤3
C.1≤k≤4 D.1<k<4
科目:czsx 来源:2011年浙江省义蓬片九年级第一次阶段考试数学卷 题型:选择
如图:等腰直角三角形ABC位于第一象限,AB=AC=2,直角
顶点A在直线y=x上,其中A点的横坐标为1,且两条直角边AB、AC分别平行于x轴、y轴,若双曲线 (k≠0)与
(k≠0)与 有交点,则k的取值范围是( )
有交点,则k的取值范围是( )
A.1<k<2 B.1≤k≤3
C.1≤k≤4 D.1<k<4

科目:czsx 来源: 题型:填空题
 如图,等腰直角三角形ABC位于第一象限,AB=AC=2,直角顶点A在直线y=x上,其中A点的横坐标为1,且两条直角边AB、AC分别平行于x轴、y轴,若双曲线y=
如图,等腰直角三角形ABC位于第一象限,AB=AC=2,直角顶点A在直线y=x上,其中A点的横坐标为1,且两条直角边AB、AC分别平行于x轴、y轴,若双曲线y= (k≠0)与△ABC有交点,则k的取值范围是________.
(k≠0)与△ABC有交点,则k的取值范围是________.