
科目:czsx 来源:陕西省西安市2016-2017学年八年级上学期期中考试数学试卷(解析版) 题型:判断题
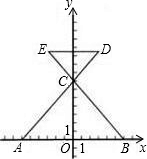
如图,直线 与
与 轴相交于点
轴相交于点 ,直线
,直线 经过点
经过点 ,与
,与 轴交于点
轴交于点 ,与
,与 轴交于点
轴交于点 ,与直线
,与直线 相交于点
相交于点 .
.

(1)求直线 的函数关系式;
的函数关系式;
(2)点 是
是
 上的一点,若
上的一点,若 的面积等于
的面积等于 的面积的
的面积的 倍,求点
倍,求点 的坐标;
的坐标;
(3)设点 的坐标为
的坐标为 ,是否存在
,是否存在 的值使得
的值使得 最小?若存在,请求出点
最小?若存在,请求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
科目:czsx 来源: 题型:
 如图所示,锐角△ABC中,∠A的平分线与三角形的外接圆交于另一点A1,点B1,C1与此类似,直线AA1与B、C两角的外角平分线相交于A0,点B0、C0与此类似.求证:
如图所示,锐角△ABC中,∠A的平分线与三角形的外接圆交于另一点A1,点B1,C1与此类似,直线AA1与B、C两角的外角平分线相交于A0,点B0、C0与此类似.求证:科目:czsx 来源:2011-2012学年山东潍坊七年级下学期期中质量检测数学试卷(带解析) 题型:解答题
如图,直线 、
、 相交于
相交于 ,
, ,且
,且 的度数是
的度数是 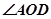 的4倍.
的4倍.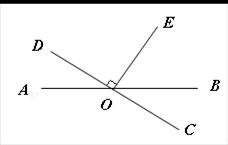
求:(1) 、
、 的度数;
的度数;
(2) 的度数.
的度数.
科目:czsx 来源: 题型:解答题
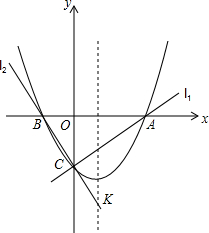 已知两直线l1、l2分别经过点A(3,0),点B(-1,0),并且当两条直线同时相交于y轴负半轴的点C时,恰好有l1⊥l2,经过点A、B、C的抛物线的对称轴与直线l2交于点K,如图所示.
已知两直线l1、l2分别经过点A(3,0),点B(-1,0),并且当两条直线同时相交于y轴负半轴的点C时,恰好有l1⊥l2,经过点A、B、C的抛物线的对称轴与直线l2交于点K,如图所示. 倍?若存在,求出点P的坐标;若不存在,请说明理由.
倍?若存在,求出点P的坐标;若不存在,请说明理由.科目:czsx 来源: 题型:
| AC | BD |
科目:czsx 来源: 题型:
| 1 | 2 |
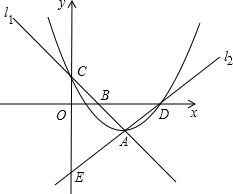 标轴分别交于B,C两点,l2与坐标轴分别交于D,E两点.
标轴分别交于B,C两点,l2与坐标轴分别交于D,E两点.科目:czsx 来源: 题型:
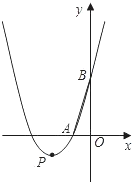 点B,tan∠ABO=
点B,tan∠ABO=| 1 |
| 3 |
| b |
| 2a |
| b |
| 2a |
| 4ac-b2 |
| 4a |
科目:czsx 来源: 题型:
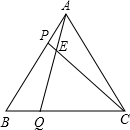 重合),且AP=BQ,AQ、CP相交于点E.
重合),且AP=BQ,AQ、CP相交于点E.科目:czsx 来源: 题型:
| 3 |
 长AC到点D,使CD=
长AC到点D,使CD=| 1 |
| 2 |
科目:czsx 来源: 题型:
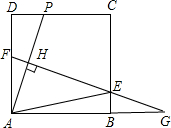 如图,己知正方形ABCD的边长为12,点P为CD边上的一个动点(点P与D、C不重合),AP的垂直平分线EF分别交AD、AP、BC于点F、H、E,交AB的延长线于点G.
如图,己知正方形ABCD的边长为12,点P为CD边上的一个动点(点P与D、C不重合),AP的垂直平分线EF分别交AD、AP、BC于点F、H、E,交AB的延长线于点G.科目:czsx 来源: 题型:
| 2 |
| 2 |
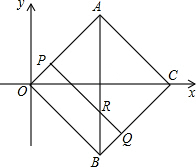 ,两点运动到相遇停止.设△OPQ的面积为S.请求出S关于t的函数关系式以及自变量t的取值范围.
,两点运动到相遇停止.设△OPQ的面积为S.请求出S关于t的函数关系式以及自变量t的取值范围.科目:czsx 来源: 题型:
科目:czsx 来源: 题型:

科目:czsx 来源: 题型:
| 6 |
| x |
| 3 |
| 2 |
| 6 |
| x |
科目:czsx 来源: 题型:
 如图,已知抛物线y=(
如图,已知抛物线y=(| 1 |
| 2 |
| 2 |