科目:czsx 来源:不详 题型:解答题

科目:czsx 来源:2014年北京市房山区中考二模数学试卷(解析版) 题型:解答题
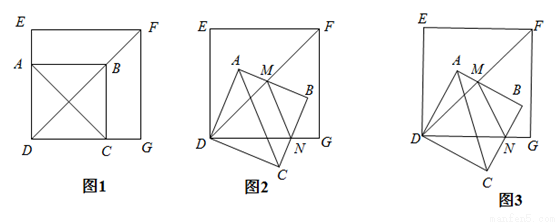
边长为2的正方形ABCD的两顶点A、C分别在正方形EFGH的两边DE、DG上(如图1),现将正方形ABCD绕D点顺时针旋转,当A点第一次落在DF上时停止旋转,旋转过程中, AB边交DF于点M,BC边交DG于点N.
(1)求边DA在旋转过程中所扫过的面积;
(2)旋转过程中,当MN和AC平行时(如图2),求正方形ABCD旋转的度数;
(3)如图3,设△MBN的周长为p,在旋转正方形ABCD的过程中,p值是否有变化?请证明你的结论.
科目:czsx 来源:解题升级 解题快速反应一典通 九年级级数学 题型:044
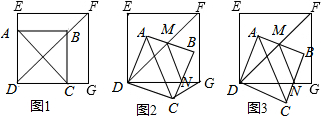
两个边长为1的正方形,其中一个正方形的顶点与另一个正方形的中心重合,如图所示,若正方形ABCD不动,另一个正方形EFGH绕其中的E点旋转.在旋转的过程中,两个正方形重叠部分面积是否发生变化?证明你的结论.

科目:czsx 来源: 题型:解答题
科目:czsx 来源: 题型:解答题

科目:czsx 来源:2012年初中毕业升学考试(福建龙岩卷)数学(带解析) 题型:解答题
如图1,过△ABC的顶点A作高AD,将点A折叠到点D(如图2),这时EF为折痕,且△BED和△CFD都是等腰三角形,再将△BED和△CFD沿它们各自的对称轴EH、FG折叠,使B、C两点都与点D重合,得到一个矩形EFGH(如图3),我们称矩形EFGH为△ABC的边BC上的折合矩形. 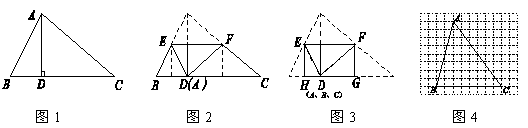
(1)若△ABC的面积为6,则折合矩形EFGH的面积为 ;
(2)如图4,已知△ABC,在图4中画出△ABC的边BC上的折合矩形EFGH;
(3)如果△ABC的边BC上的折合矩形EFGH是正方形,且BC=2a,那么,BC边上的高AD= ,正方形EFGH的对角线长为 .
科目:czsx 来源:2012年初中毕业升学考试(福建龙岩卷)数学(解析版) 题型:解答题
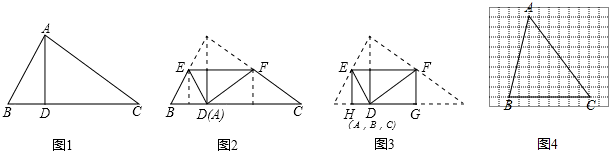
如图1,过△ABC的顶点A作高AD,将点A折叠到点D(如图2),这时EF为折痕,且△BED和△CFD都是等腰三角形,再将△BED和△CFD沿它们各自的对称轴EH、FG折叠,使B、C两点都与点D重合,得到一个矩形EFGH(如图3),我们称矩形EFGH为△ABC的边BC上的折合矩形.
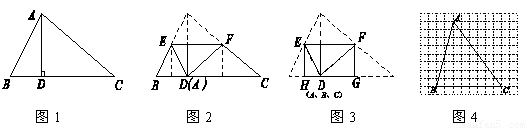
(1)若△ABC的面积为6,则折合矩形EFGH的面积为 ;
(2)如图4,已知△ABC,在图4中画出△ABC的边BC上的折合矩形EFGH;
(3)如果△ABC的边BC上的折合矩形EFGH是正方形,且BC=2a,那么,BC边上的高AD= ,正方形EFGH的对角线长为 .
科目:czsx 来源: 题型:解答题
科目:czsx 来源:2012年福建省龙岩市中考数学试卷(解析版) 题型:解答题
科目:czsx 来源:不详 题型:解答题

科目:czsx 来源: 题型:
如图①,矩形EFGH的两个顶点E和F在y轴上,顶点H的坐标为(6,3),顶点G的坐标为(-6,3),动点A从(-6,0)出发,以每秒3个单位长度的速度沿x轴的正方向匀速运动,与此同时动点C从点O(0,0)出发,沿x轴的正方向作匀速运动,当点A运动到GH边上时,点C和A一起停止运动.在运动过程中,以CA为对角线作正方形.设该正方形和矩形EFGH重叠部分的面积为S,运动时间为t秒,S与t的部分函数图象如图②所示
(1)点A的运动速度为每秒 单位长度。(直接写出答案)
(2)在上述运动过程中,求S关于t的函数关系式,并把函数图象补完整。
(3)当t= 秒时,重叠部分面积S最大,最大面积是 平方单位.;
(4)当重叠部分面积S不小于1 平方单位时,t的取值范围是 .
(第(3)、(4)题直接写出答案)

科目:czsx 来源:新教材完全解读 九年级数学 (下册) (配华东师大版新课标) 华东师大版新课标 题型:059
已知如图所示,正方形ABCD的周长为4a,四边形EFGH的四个顶点E,F,G,H分别在AB,BC,CD,DA上滑动,在滑动过程中,始终有EH∥BD∥FG,且EH=FG,那么四边形EFGH的周长是否可求?若能求出,它的周长是多少;若不能求出,请说明理由.

科目:czsx 来源: 题型:解答题
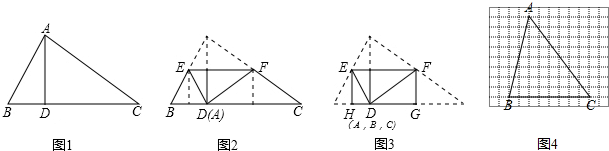
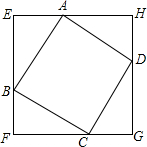 如图,正方形ABCD的四个顶点分别在正方形EFGH的四条边上,我们称正方形EFGH是正方形ABCD的外接正方形.
如图,正方形ABCD的四个顶点分别在正方形EFGH的四条边上,我们称正方形EFGH是正方形ABCD的外接正方形.科目:czsx 来源: 题型:
| 2 |
| 2 |
科目:czsx 来源: 题型:阅读理解
问题提出
我们在分析解决某些数学问题时,经常要比较两个数或代数式的大小,而解决问题的策略一般要进行一定的转化,其中“作差法”就是常用的方法之一.所谓“作差法”:就是通过作差、变形,并利用差的符号确定他们的大小,即要比较代数式M、N的大小,只要作出它们的差M-N,若M-N>0,则M>N;若M-N=0,则M=N;若M-N<0,则M<N.
问题解决
如图1,把边长为a+b(a≠b)的大正方形分割成两个边长分别是a、b的小正方形及两个矩形,试比较两个小正方形面积之和M与两个矩形面积之和N的大小.
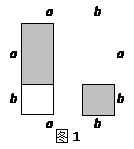
解:由图可知:M=a2+b2,N=2ab.
∴M-N=a2+b2-2ab=(a-b)2.
∵a≠b,∴(a-b)2>0.
∴M-N>0.
∴M>N.
类比应用
1.已知:多项式M =2a2-a+1 ,N =a2-2a .试比较M与N的大小.
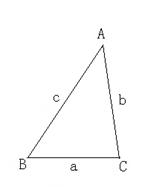
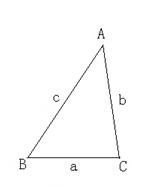
2.已知:如图,锐角△ABC (其中BC为a,AC为b,AB为c)三边
满足a <b < c ,现将△ABC 补成长方形,使得△ABC的两个顶
点为长方形的两个端点,第三个顶点落在长方形的这一边的对边上。
①这样的长方形可以画 个;
②所画的长方形中哪个周长最小?为什么?
拓展延伸
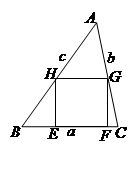
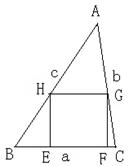
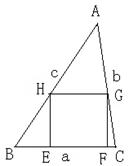
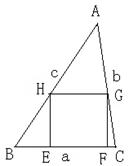
已知:如图,锐角△ABC (其中BC为a,AC为b,AB为c)三边满足a <b < c ,画其BC边上的内接正方形EFGH , 使E、F两点在边BC上,G、H分别在边AC、AB上,同样还可画AC、AB边上的内接正方形,问哪条边上的内接正方形面积最大?为什么?
科目:czsx 来源: 题型:阅读理解

科目:czsx 来源:2012届江苏盐城盐都区九年级下学期期中质量检测数学试卷(带解析). 题型:解答题
问题提出
我们在分析解决某些数学问题时,经常要比较两个数或代数式的大小,而解决问题的策略一般要进行一定的转化,其中“作差法”就是常用的方法之一.所谓“作差法”:就是通过作差、变形,并利用差的符号确定他们的大小,即要比较代数式M、N的大小,只要作出它们的差M-N,若M-N>0,则M>N;若M-N=0,则M=N;若M-N<0,则M<N.
问题解决
如图1,把边长为a+b(a≠b)的大正方形分割成两个边长分别是a、b的小正方形及两个矩形,试比较两个小正方形面积之和M与两个矩形面积之和N的大小.
解:由图可知:M=a2+b2,N=2ab.
∴M-N=a2+b2-2ab=(a-b)2.
∵a≠b,∴(a-b)2>0.
∴M-N>0.
∴M>N.
类比应用
【小题1】已知:多项式M =2a2-a+1 ,N =a2-2a.试比较M与N的大小.
【小题2】已知:如图,锐角△ABC (其中BC为a,AC为b,AB为c)三边
满足a <b < c ,现将△ABC 补成长方形,使得△ABC的两个顶
点为长方形的两个端点,第三个顶点落在长方形的这一边的对边上。
①这样的长方形可以画 个;
②所画的长方形中哪个周长最小?为什么?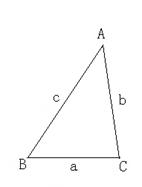
拓展延伸
已知:如图,锐角△ABC (其中BC为a,AC为b,AB为c)三边满足a <b < c ,画其BC边上的内接正方形EFGH , 使E、F两点在边BC上,G、H分别在边AC、AB上,同样还可画AC、AB边上的内接正方形,问哪条边上的内接正方形面积最大?为什么?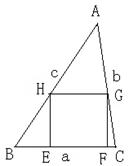
科目:czsx 来源:2011-2012学年江苏盐城盐都区九年级下学期期中质量检测数学试卷(解析版). 题型:解答题
问题提出
我们在分析解决某些数学问题时,经常要比较两个数或代数式的大小,而解决问题的策略一般要进行一定的转化,其中“作差法”就是常用的方法之一.所谓“作差法”:就是通过作差、变形,并利用差的符号确定他们的大小,即要比较代数式M、N的大小,只要作出它们的差M-N,若M-N>0,则M>N;若M-N=0,则M=N;若M-N<0,则M<N.
问题解决
如图1,把边长为a+b(a≠b)的大正方形分割成两个边长分别是a、b的小正方形及两个矩形,试比较两个小正方形面积之和M与两个矩形面积之和N的大小.
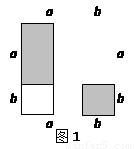
解:由图可知:M=a2+b2,N=2ab.
∴M-N=a2+b2-2ab=(a-b)2.
∵a≠b,∴(a-b)2>0.
∴M-N>0.
∴M>N.
类比应用
1.已知:多项式M =2a2-a+1 ,N =a2-2a .试比较M与N的大小.
2.已知:如图,锐角△ABC (其中BC为a,AC为b,AB为c)三边
满足a <b < c ,现将△ABC 补成长方形,使得△ABC的两个顶
点为长方形的两个端点,第三个顶点落在长方形的这一边的对边上。
①这样的长方形可以画 个;
②所画的长方形中哪个周长最小?为什么?
拓展延伸
已知:如图,锐角△ABC (其中BC为a,AC为b,AB为c)三边满足a <b < c ,画其BC边上的内接正方形EFGH , 使E、F两点在边BC上,G、H分别在边AC、AB上,同样还可画AC、AB边上的内接正方形,问哪条边上的内接正方形面积最大?为什么?
科目:czsx 来源:2013届江苏省江阴市长泾片九年级上学期期末考试数学试卷(带解析) 题型:解答题
【问题提出】我们在分析解决某些数学问题时,经常要比较两个数或代数式的大小,而解决问题的策略一般要进行一定的转化,其中“作差法”就是常用的方法之一.所谓“作差法”:就是通过作差、变形,并利用差的符号确定他们的大小,即要比较代数式M、N的大小,只要作出它们的差M-N,若M-N>0,则M>N;若M-N=0,则M=N;若M-N<0,则M<N.
【问题解决】如图1,把边长为a+b(a≠b)的大正方形分割成两个边长分别是a、b的小正方形及两个矩形,试比较两个小正方形面积之和M与两个矩形面积之和N的大小.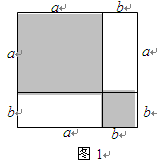
解:由图可知: ,
, .
.
∴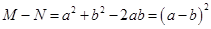 .
.
∵a≠b,∴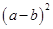 >0.
>0.
∴M-N>0.∴M>N.
【类比应用】(1)已知:多项式M =2a2-a+1 ,N =a2-2a .
试比较M与N的大小.
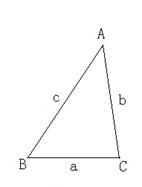
(2)已知:如图2,锐角△ABC (其中BC为a ,AC为 b,
AB为c)三边满足a <b < c ,现将△ABC 补成长方形,
使得△ABC的两个顶点为长方形的两个端点,第三个顶点落
在长方形的这一边的对边上。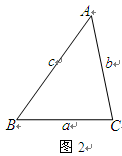
①这样的长方形可以画 个;
②所画的长方形中哪个周长最小?为什么?
【拓展延伸】 已知:如图,锐角△ABC (其中BC为a,AC为b,AB为c)三边满足a <b < c ,画其BC边上的内接正方形EFGH , 使E、F两点在边BC上,G、H分别在边AC、AB上,同样还可画AC、AB边上的内接正方形,问哪条边上的内接正方形面积最大?为什么?