练习册

  • 练习册
  • 试题
    精英家教网 > 试题搜索列表 >90-去一个数字的7

    90-去一个数字的7答案解析

    科目：czsx 来源： 题型：

    一个不透明的盒子中放有4张扑克牌，牌面上的数字分别3，4，5，x，这些扑克牌除数字外都相同．甲、乙两人每次同时从盒子中各随机摸出1张牌，并计算摸出的这2张牌面上的数字之和．记录后都将牌放回盒子中搅匀，进行重复实验．实验数据如下表：
    摸牌总次数 10 20 30 60 90 120 180 240 330 450
    “和为9”出现的频数 1 9 14 24 26 37 58 82 109 150
    “和为9”出现的频率 0.10 0.45 0.47 0.40 0.29 0.31 0.32 0.34 0.33 0.33
    解答下列问题：
    （1）如果实验继续进行下去，根据上表数据，出现“和为9”的频率将稳定在它的概率附近，试估计出现“和为9”的概率；
    （2）根据（1），若x是不等于3，4，5的自然数，试求x的值．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    一个不透明的袋子中装有4个质地、大小均相同的小球，这些小球上分别标有数字3、4、5、x．甲、乙两人每次从袋中各随机摸出1球，并计算摸出这2个小球上数字之和，记录后都将放回袋中搅匀，进行重复实验．实验数据如下表：
    摸球总次数
    		10
    		20
    		30
    		60
    		90
    		120
    		180
    		240
    		330
    		450
    “和为8”出现频数
    		2
    		10
    		13
    		24
    		30
    		37
    		58
    		82
    		110
    		150
    “和为8”出现频率
    		0.20
    		0.50
    		0.43
    		0.40
    		0.33
    		0.31
    		0.32
    		0.34
    		0.33
    		0.33
    解答下列问题：
    (1)如果实验继续进行下去，根据上表数据，出现“和为8”频率将稳定在它概率附近．估计
    出现“和为8”概率是________．
    0.33
    (2)如果摸出的这两个小球上数字之和为9概率是，那么x值可以取7吗？请用列表法或画树状图法说明理由；如果x值不可以取7，请写出一个符合要求x值．

    查看答案和解析>>

    科目：czsx 来源：2012届江苏省泰州市靖江外国语学校中考二模数学卷（带解析） 题型：解答题

    一个不透明的袋子中装有4个质地、大小均相同的小球，这些小球上分别标有数字3、4、5、x．甲、乙两人每次从袋中各随机摸出1球，并计算摸出这2个小球上数字之和，记录后都将放回袋中搅匀，进行重复实验．实验数据如下表：

    摸球总次数
    		10
    		20
    		30
    		60
    		90
    		120
    		180
    		240
    		330
    		450
    “和为8”出现频数
    		2
    		10
    		13
    		24
    		30
    		37
    		58
    		82
    		110
    		150
    “和为8”出现频率
    		0.20
    		0.50
    		0.43
    		0.40
    		0.33
    		0.31
    		0.32
    		0.34
    		0.33
    		0.33
    解答下列问题：
    (1)如果实验继续进行下去，根据上表数据，出现“和为8”频率将稳定在它概率附近．估计
    出现“和为8”概率是________．
    0.33
    (2)如果摸出的这两个小球上数字之和为9概率是，那么x值可以取7吗？请用列表法或画树状图法说明理由；如果x值不可以取7，请写出一个符合要求x值．

    查看答案和解析>>

    科目：czsx 来源： 题型：解答题

    一个不透明的盒子中放有4张扑克牌，牌面上的数字分别3，4，5，x，这些扑克牌除数字外都相同．甲、乙两人每次同时从盒子中各随机摸出1张牌，并计算摸出的这2张牌面上的数字之和．记录后都将牌放回盒子中搅匀，进行重复实验．实验数据如下表：
    摸牌总次数1020306090120180240330450
    “和为9”出现的频数19142426375882109150
    “和为9”出现的频率0.100.450.470.400.290.310.320.340.330.33
    解答下列问题：
    （1）如果实验继续进行下去，根据上表数据，出现“和为9”的频率将稳定在它的概率附近，试估计出现“和为9”的概率；
    （2）根据（1），若x是不等于3，4，5的自然数，试求x的值．

    查看答案和解析>>

    科目：czsx 来源：2009年江苏省淮安市淮阴中学中考数学模拟试卷（解析版） 题型：解答题

    一个不透明的盒子中放有4张扑克牌，牌面上的数字分别3，4，5，x，这些扑克牌除数字外都相同．甲、乙两人每次同时从盒子中各随机摸出1张牌，并计算摸出的这2张牌面上的数字之和．记录后都将牌放回盒子中搅匀，进行重复实验．实验数据如下表：
    摸牌总次数1020306090120180240330450
    “和为9”出现的频数19142426375882109150
    “和为9”出现的频率0.100.450.470.400.290.310.320.340.330.33
    解答下列问题：
    （1）如果实验继续进行下去，根据上表数据，出现“和为9”的频率将稳定在它的概率附近，试估计出现“和为9”的概率；
    （2）根据（1），若x是不等于3，4，5的自然数，试求x的值．

    查看答案和解析>>

    科目：czsx 来源：2010年北京市实验外国语学校中考数学模拟试卷（解析版） 题型：解答题

    一个不透明的盒子中放有4张扑克牌，牌面上的数字分别3，4，5，x，这些扑克牌除数字外都相同．甲、乙两人每次同时从盒子中各随机摸出1张牌，并计算摸出的这2张牌面上的数字之和．记录后都将牌放回盒子中搅匀，进行重复实验．实验数据如下表：
    摸牌总次数1020306090120180240330450
    “和为9”出现的频数19142426375882109150
    “和为9”出现的频率0.100.450.470.400.290.310.320.340.330.33
    解答下列问题：
    （1）如果实验继续进行下去，根据上表数据，出现“和为9”的频率将稳定在它的概率附近，试估计出现“和为9”的概率；
    （2）根据（1），若x是不等于3，4，5的自然数，试求x的值．

    查看答案和解析>>

    科目：czsx 来源：2009年江苏省连云港市中考数学原创试卷大赛（21）（解析版） 题型：解答题

    一个不透明的盒子中放有4张扑克牌，牌面上的数字分别3，4，5，x，这些扑克牌除数字外都相同．甲、乙两人每次同时从盒子中各随机摸出1张牌，并计算摸出的这2张牌面上的数字之和．记录后都将牌放回盒子中搅匀，进行重复实验．实验数据如下表：
    摸牌总次数1020306090120180240330450
    “和为9”出现的频数19142426375882109150
    “和为9”出现的频率0.100.450.470.400.290.310.320.340.330.33
    解答下列问题：
    （1）如果实验继续进行下去，根据上表数据，出现“和为9”的频率将稳定在它的概率附近，试估计出现“和为9”的概率；
    （2）根据（1），若x是不等于3，4，5的自然数，试求x的值．

    查看答案和解析>>

    科目：czsx 来源：不详 题型：解答题

    一个不透明的袋子中装有4个质地、大小均相同的小球，这些小球上分别标有数字3、4、5、x．甲、乙两人每次从袋中各随机摸出1球，并计算摸出这2个小球上数字之和，记录后都将放回袋中搅匀，进行重复实验．实验数据如下表：
    摸球总次数
    		10
    		20
    		30
    		60
    		90
    		120
    		180
    		240
    		330
    		450
    “和为8”出现频数
    		2
    		10
    		13
    		24
    		30
    		37
    		58
    		82
    		110
    		150
    “和为8”出现频率
    		0.20
    		0.50
    		0.43
    		0.40
    		0.33
    		0.31
    		0.32
    		0.34
    		0.33
    		0.33
    解答下列问题：
    (1)如果实验继续进行下去，根据上表数据，出现“和为8”频率将稳定在它概率附近．估计
    出现“和为8”概率是________．
    0.33
    (2)如果摸出的这两个小球上数字之和为9概率是，那么x值可以取7吗？请用列表法或画树状图法说明理由；如果x值不可以取7，请写出一个符合要求x值．

    查看答案和解析>>

    科目：czsx 来源：2011-2012学年江苏省泰州市靖江外国语学校中考二模数学卷（解析版） 题型：解答题

    一个不透明的袋子中装有4个质地、大小均相同的小球，这些小球上分别标有数字3、4、5、x．甲、乙两人每次从袋中各随机摸出1球，并计算摸出这2个小球上数字之和，记录后都将放回袋中搅匀，进行重复实验．实验数据如下表：

    摸球总次数

    10

    20

    30

    60

    90

    120

    180

    240

    330

    450

    “和为8”出现频数

    2

    10

    13

    24

    30

    37

    58

    82

    110

    150

    “和为8”出现频率

    0.20

    0.50

    0.43

    0.40

    0.33

    0.31

    0.32

    0.34

    0.33

    0.33

    解答下列问题：

    (1) 如果实验继续进行下去，根据上表数据，出现“和为8”频率将稳定在它概率附近．估计

    出现“和为8”概率是________．

    (2)如果摸出的这两个小球上数字之和为9概率是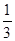，那么x值可以取7吗？请用列表法或画树状图法说明理由；如果x值不可以取7，请写出一个符合要求x值．

    【解析】(1)由于大量试验中“和为8”出现的频数稳定在0.3附近，据图表，可估计“和为8”出现的概率为3.1，3.2，3.3等均可，(2)利用概率解答

     

    查看答案和解析>>

    科目：czsx 来源： 题型：

    一个不透明的袋子中装有4个质地、大小均相同的小球，这些小球上分别标有数字3、4、5、x．甲、乙两人每次从袋中各随机摸出1球，并计算摸出这2个小球上数字之和，记录后都将放回袋中搅匀，进行重复实验．实验数据如下表：

    摸球总次数

    10

    20

    30

    60

    90

    120

    180

    240

    330

    450

    “和为8”出现频数

    2

    10

    13

    24

    30

    37

    58

    82

    110

    150

    “和为8”出现频率

    0.20

    0.50

    0.43

    0.40

    0.33

    0.31

    0.32

    0.34

    0.33

    0.33

    解答下列问题：

    (1) 如果实验继续进行下去，根据上表数据，出现“和为8”频率将稳定在它概率附近．估计

    出现“和为8”概率是________．

    (2)如果摸出的这两个小球上数字之和为9概率是，那么x值可以取7吗？请用列表法或画树状图法说明理由；如果x值不可以取7，请写出一个符合要求x值．

    【解析】(1)由于大量试验中“和为8”出现的频数稳定在0.3附近，据图表，可估计“和为8”出现的概率为3.1，3.2，3.3等均可，(2)利用概率解答

     

    查看答案和解析>>

    科目：czsx 来源：2014-2015学年山东省威海市乳山市中考一模数学试卷（解析版） 题型：计算题

    如图1，将一个直角三角板的直角顶点P放在正方形ABCD的对角线BD上滑动，并使其一条直角边始终经过点A，另一条直角边与BC相交于点E．

    （1）求证：PA=PE；

    （2）若将（1）中的正方形变为矩形，其余条件不变（如图2），且AD=10，DC=8，求AP：PE；

    （3）在（2）的条件下，当P滑动到BD的延长线上时（如图3），请你直接写出AP：PE的比值．

    【答案】（1）证明见解析；（2）AP：PE=5：4；（3）AP：PE=5：4；

    【解析】

    试题分析：（1）过P作PM⊥AB于M，PN⊥BC于N，四边形BMPN是正方形，得出PM=PN，∠MPN=90°，求出∠APM=∠NPE，∠AMP=∠PNE，证△APM≌△EPN，推出AP=PE即可；

    （2）证△BPM∽△BDA，△BNP∽△BCD，得出，，推出，求出，证△APM∽△EPN，推出即可；

    （3）过P作PM⊥AB于M，PN⊥BC于N，证△BPM∽△BDA，△BNP∽△BCD，得出，，推出，求出，证△APM∽△EPN，推出即可．

    试题解析：（1）证明：过P作PM⊥AB于M，PN⊥BC于N，

    ∵四边形ABCD是正方形，

    ∴∠ABD=45°，

    ∴∠MPB=45°=∠ABD，

    ∴PM=BM，

    同理BP=BN，

    ∵四边形ABCD是正方形，

    ∴∠ABC=90°=∠BMP=∠BNP，

    ∴四边形BMPN是正方形，

    ∴PM=PN，∠MPN=90°，

    ∵∠APE=90°，

    ∴都减去∠MPE得：∠APM=∠NPE，

    ∵PM⊥AB，PN⊥BC，

    ∴∠AMP=∠PNE，

    在△APM和△EPN中

    ∴△APM≌△EPN（ASA），

    ∴AP=PE；

    （2）【解析】
    ∵四边形ABCD是矩形，

    ∴∠BAD=∠C=90°，

    ∵∠PMB=PNB=90°，

    ∴PM∥AD，PN∥CD，

    ∴△BPM∽△BDA，△BNP∽△BCD，

    ∴，，，

    ∴，

    ∴，

    ∵∠AMP=∠ENP=90°，∠MPA=∠EPN，

    ∴△APM∽△EPN，

    ∴=，

    AP：PE=5：4；

    （3）【解析】
    AP：PE=5：4．

    考点：相似形综合题．

    【题型】解答题
    【适用】一般
    【标题】2015届山东省威海市乳山市中考一模数学试卷（带解析）
    【关键字标签】
    【结束】
     

    如图，直线y=-x+2与x轴交于点B，与y轴交于点C，已知二次函数的图象经过点B，C和点A（-1，0）．

    （1）求B，C两点坐标；

    （2）求该二次函数的关系式；

    （3）若抛物线的对称轴与x轴的交点为点D，点E是线段BC上的一个动点，过点E作x轴的垂线与抛物线相交于点F，当点E运动到什么位置时，四边形CDBF的面积最大？求出四边形CDBF的最大面积及此时E点的坐标；

    （4）在抛物线的对称轴上是否存在点P，使△PCD是以CD为腰的等腰三角形？如果存在，直接写出P点的坐标；如果不存在，请说明问题．

    查看答案和解析>>

    科目：czsx 来源：学习周报　数学　华师大七年级版　2009－2010学年　第15期　总第171期 华师大版 题型：044

    下午上课时，数学老师有急事要去处理，匆忙之间在黑板上布置了一个如下的题目：

    如图，∠AOB＝90°，∠BOC＝30°，OM平分∠AOC，ON平分∠BOC，求∠MON的度数．

    因为老师写字过快导致潦草，甲同学将∠AOB的度数看错了，结果求得∠MON的度数等于∠AOB的错误的度数的一半；而乙同学把∠BOC的度数抄错了，求出的结果却是正确的．

    问题(1)：你知道这是为什么吗？从甲、乙两位同学的结果中，你能看出什么规律？

    问题(2)：线段的计算与角的计算存在着紧密的联系，它们之间可以互相借鉴解法．你能模仿此题的规律设计一个以线段为背景的计算题吗？请写出你所设计的题的规律．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    一只不透明的袋子中装有4个小球，分别标有数字2，3，4，x，这些球除数字外都相同．甲、乙两人每次同时从袋中各随机摸出1个球，并计算摸出的这2个小球上数字之和．记录后都将小球放回袋中搅匀，进行重复实验．实验数据如下表：解答下列问题：
    （1）如果实验继续进行下去，根据上表数据，出现“和为7”的概率将稳定在它的概率附近，试估计出现“和为7”的概率；
    （2）根据（1），若x是不等于2，3，4的自然数，试求x的值．
     摸球总次数  10 20   30  60  90  120  180  240 330  450 
    “和为7”出现的频次  1  9  14  24  26  37 58  82  109  150
    “和为7”出现的频率  0.10  0.45  0.47  0.40  0.29  0.31  0.32  0.34  0.33  0.33

    查看答案和解析>>

    科目：czsx 来源： 题型：

    一只不透明的袋子中装有4个小球，分别标有数字2、3、4、x，这些球除数字外都相同．甲、乙两人每次同时从袋中各随机摸出1个球，并计算摸出的这2个小球上数字之和，记录后都将小球放回袋中搅匀，进行重复实验．实验数据如下表：

    摸球总次数

    10

    20

    30

    60

    90

    120

    180

    240

    330

    450

    “和为7”出现的频数

    1

    9

    14

    24

    26

    37

    58

    82

    109

    150

    “和为7”出现的频率

    0.10

    0.45

    0.47

    0.40

    0.29

    0.31

    0.32

    0.34

    0.33

    0.33

    解答下列问题：

    （1）如果实验继续进行下去，根据上表数据，出现“和为7”的频率将稳定在它的概

    率附近．试估计出现“和为7”的概率；

    （2）根据（1），若x是不等于2、3、4的自然数，试求x的值．

    查看答案和解析>>

    科目：czsx 来源：第6章《频率与概率》中考题集（14）：6.3 生日相同的概率（解析版） 题型：解答题

    一只不透明的袋子中装有4个小球，分别标有数字2，3，4，x，这些球除数字外都相同．甲、乙两人每次同时从袋中各随机摸出1个球，并计算摸出的这2个小球上数字之和．记录后都将小球放回袋中搅匀，进行重复实验．实验数据如下表：解答下列问题：
    （1）如果实验继续进行下去，根据上表数据，出现“和为7”的概率将稳定在它的概率附近，试估计出现“和为7”的概率；
    （2）根据（1），若x是不等于2，3，4的自然数，试求x的值．
     摸球总次数 1020  30 60 90 120 180 240330 450 
    “和为7”出现的频次 1 9 14 24 26 3758 82 109 150
    “和为7”出现的频率 0.10 0.45 0.47 0.40 0.29 0.31 0.32 0.34 0.33 0.33

    查看答案和解析>>

    科目：czsx 来源：第23章《概率的求法与应用》中考题集（27）：23.1 求概率的方法（解析版） 题型：解答题

    一只不透明的袋子中装有4个小球，分别标有数字2，3，4，x，这些球除数字外都相同．甲、乙两人每次同时从袋中各随机摸出1个球，并计算摸出的这2个小球上数字之和．记录后都将小球放回袋中搅匀，进行重复实验．实验数据如下表：解答下列问题：
    （1）如果实验继续进行下去，根据上表数据，出现“和为7”的概率将稳定在它的概率附近，试估计出现“和为7”的概率；
    （2）根据（1），若x是不等于2，3，4的自然数，试求x的值．
     摸球总次数 1020  30 60 90 120 180 240330 450 
    “和为7”出现的频次 1 9 14 24 26 3758 82 109 150
    “和为7”出现的频率 0.10 0.45 0.47 0.40 0.29 0.31 0.32 0.34 0.33 0.33

    查看答案和解析>>

    科目：czsx 来源：第33章《概率的计算和估计》中考题集（28）：33.3 概率的估计（解析版） 题型：解答题

    一只不透明的袋子中装有4个小球，分别标有数字2，3，4，x，这些球除数字外都相同．甲、乙两人每次同时从袋中各随机摸出1个球，并计算摸出的这2个小球上数字之和．记录后都将小球放回袋中搅匀，进行重复实验．实验数据如下表：解答下列问题：
    （1）如果实验继续进行下去，根据上表数据，出现“和为7”的概率将稳定在它的概率附近，试估计出现“和为7”的概率；
    （2）根据（1），若x是不等于2，3，4的自然数，试求x的值．
     摸球总次数 1020  30 60 90 120 180 240330 450 
    “和为7”出现的频次 1 9 14 24 26 3758 82 109 150
    “和为7”出现的频率 0.10 0.45 0.47 0.40 0.29 0.31 0.32 0.34 0.33 0.33

    查看答案和解析>>

    科目：czsx 来源：第5章《概率的计算》中考题集（01）：5.1 用频率估计概率（解析版） 题型：解答题

    一只不透明的袋子中装有4个小球，分别标有数字2，3，4，x，这些球除数字外都相同．甲、乙两人每次同时从袋中各随机摸出1个球，并计算摸出的这2个小球上数字之和．记录后都将小球放回袋中搅匀，进行重复实验．实验数据如下表：解答下列问题：
    （1）如果实验继续进行下去，根据上表数据，出现“和为7”的概率将稳定在它的概率附近，试估计出现“和为7”的概率；
    （2）根据（1），若x是不等于2，3，4的自然数，试求x的值．
     摸球总次数 1020  30 60 90 120 180 240330 450 
    “和为7”出现的频次 1 9 14 24 26 3758 82 109 150
    “和为7”出现的频率 0.10 0.45 0.47 0.40 0.29 0.31 0.32 0.34 0.33 0.33

    查看答案和解析>>

    科目：czsx 来源：第26章《随机事件的概率》中考题集（31）：26.2 模拟实验（解析版） 题型：解答题

    一只不透明的袋子中装有4个小球，分别标有数字2，3，4，x，这些球除数字外都相同．甲、乙两人每次同时从袋中各随机摸出1个球，并计算摸出的这2个小球上数字之和．记录后都将小球放回袋中搅匀，进行重复实验．实验数据如下表：解答下列问题：
    （1）如果实验继续进行下去，根据上表数据，出现“和为7”的概率将稳定在它的概率附近，试估计出现“和为7”的概率；
    （2）根据（1），若x是不等于2，3，4的自然数，试求x的值．
     摸球总次数 1020  30 60 90 120 180 240330 450 
    “和为7”出现的频次 1 9 14 24 26 3758 82 109 150
    “和为7”出现的频率 0.10 0.45 0.47 0.40 0.29 0.31 0.32 0.34 0.33 0.33

    查看答案和解析>>

    科目：czsx 来源：第25章《概率初步》中考题集（38）：25.3 利用频率估计概率（解析版） 题型：解答题

    一只不透明的袋子中装有4个小球，分别标有数字2，3，4，x，这些球除数字外都相同．甲、乙两人每次同时从袋中各随机摸出1个球，并计算摸出的这2个小球上数字之和．记录后都将小球放回袋中搅匀，进行重复实验．实验数据如下表：解答下列问题：
    （1）如果实验继续进行下去，根据上表数据，出现“和为7”的概率将稳定在它的概率附近，试估计出现“和为7”的概率；
    （2）根据（1），若x是不等于2，3，4的自然数，试求x的值．
     摸球总次数 1020  30 60 90 120 180 240330 450 
    “和为7”出现的频次 1 9 14 24 26 3758 82 109 150
    “和为7”出现的频率 0.10 0.45 0.47 0.40 0.29 0.31 0.32 0.34 0.33 0.33

    查看答案和解析>>