
科目:czsx 来源: 题型:解答题
科目:czwl 来源: 题型:选择题
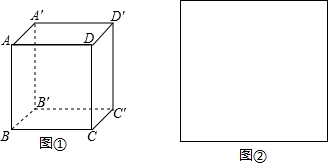
 如图所示,一个质量均匀的斜四棱柱,斜楞长21厘米,其底面为正四方形,边宽10厘米,斜楞与竖直方向的夹角为θ=30°.斜四棱柱的上端靠着光滑的竖直墙壁,底部置于粗糙的水平地面上,处于平衡状态.该物体受到作用力共有( )
如图所示,一个质量均匀的斜四棱柱,斜楞长21厘米,其底面为正四方形,边宽10厘米,斜楞与竖直方向的夹角为θ=30°.斜四棱柱的上端靠着光滑的竖直墙壁,底部置于粗糙的水平地面上,处于平衡状态.该物体受到作用力共有( )| A. | 二个 | B. | 三个 | C. | 四个 | D. | 五个 |
科目:czsx 来源: 题型:
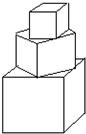 有一塔形几何体由若干个正方体构成,构成方式如图所示:上层正方体底面的四个顶点恰好是下层正方体上底面各边的中点.已知最底层正方体的棱长为2,且该塔形几何体的全面积(含最底层正方体的底面面积)超过39,则该塔形中正方体的个数至少是( )
有一塔形几何体由若干个正方体构成,构成方式如图所示:上层正方体底面的四个顶点恰好是下层正方体上底面各边的中点.已知最底层正方体的棱长为2,且该塔形几何体的全面积(含最底层正方体的底面面积)超过39,则该塔形中正方体的个数至少是( )| A、4 | B、5 | C、6 | D、7 |
科目:czsx 来源: 题型:
 有一塔形几何体由若干个正方体构成,构成方式如图所示:上层正方体底面的四个顶点恰好是下层正方体上底面各边的中点.已知最底层正方体的棱长为8,且该塔形几何体的全面积(含最底层正方体的底面面积)超过639,则该塔形中正方体的个数至少是
有一塔形几何体由若干个正方体构成,构成方式如图所示:上层正方体底面的四个顶点恰好是下层正方体上底面各边的中点.已知最底层正方体的棱长为8,且该塔形几何体的全面积(含最底层正方体的底面面积)超过639,则该塔形中正方体的个数至少是科目:gzsx 来源: 题型:
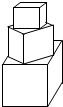 有一塔形几何体由若干个正方体构成,构成方式如图所示,上层正方体下底面的四个顶点是下层正方体上底面各边的中点.已知最底层正方体的棱长为2,且该塔形的表面积(含最底层正方体的底面面积)超过39,则该塔形中正方体的个数至少是( )
有一塔形几何体由若干个正方体构成,构成方式如图所示,上层正方体下底面的四个顶点是下层正方体上底面各边的中点.已知最底层正方体的棱长为2,且该塔形的表面积(含最底层正方体的底面面积)超过39,则该塔形中正方体的个数至少是( )| A、4 | B、5 | C、6 | D、7 |
科目:gzsx 来源:数学教研室 题型:013
有一塔形几何体由若干个正方体构成,构成方式如图所示,上层正方体下底面的四项点是下层正方体上底面各边的中点.已知最底层正方体的棱长为2,且该塔形的表面积(含最底层正方体的底面面积)超过39,则该塔形中正方体的个数至少是
[ ]

科目:gzsx 来源: 题型:013
有一塔形几何体由若干个正方体构成,构成方式如图所示,上层正方体下底面的四项点是下层正方体上底面各边的中点.已知最底层正方体的棱长为2,且该塔形的表面积(含最底层正方体的底面面积)超过39,则该塔形中正方体的个数至少是
[
]
|
A .4 |
B .5 |
|
C .6 |
D .7 |
科目:gzsx 来源:2008年高考预测卷理科数学(广东卷)全国通用 题型:013
有一塔形几何体由若干个正方体构成,构成方式如图所示,上层正方体下底面的四个顶点是下层正方体上底面各边的中点.已知最底层正方体的棱长为2,且该塔形的表面积(含最底层正方体的底面面积)超过39,则该塔形中正方体的个数至少是

A.4
B.5
C.6
D.7
科目:gzsx 来源: 题型:

A.4 B.5
C.6 D.7
科目:gzsx 来源: 题型:
有一塔形几何体由若干个正方体构成,构成方式如图所示,上层正方体下底面的四个顶点是下层正方体上底面各边的中点。已知最底层正方体的棱长为2,且该塔形的表面积(含最底层正方体的底面面积)超过39,则该塔形中正方体的个数至少是 ( )
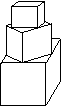 A 4;
A 4;
B 5;
C 6;
D 7;
科目:gzsx 来源:2011-2012学年安徽省蚌埠四校联盟高一自主招生考试数学试卷(解析版) 题型:填空题
有一塔形几何体由若干个正方体构成,构成方式如图所示,上层正方体下底面的四个顶点是下层正方体上底面各边的中点.已知最底层正方体的棱长为2,且该塔形的表面积(含最底层正方体的底面面积)超过39,则该塔形中正方体的个数至少是___________.
科目:gzsx 来源:2010-2011年安徽省高一第二学期期中考试数学试卷 题型:选择题
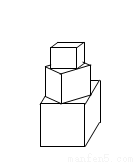
有一塔形几何体由若干个正方体构成,构成方式如图所示,上层正方体下底面的四个顶点是下层正方体上底面各边的中点。已知最底层正方体的棱长为2,且该塔形的表面积(含最底层正方体的底面面积)超过39,则该塔形中正方体的个数至少是
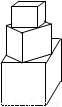
A. 4 B .5 C .6 D .7
科目:czsx 来源: 题型:填空题
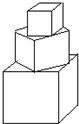 有一塔形几何体由若干个正方体构成,构成方式如图所示:上层正方体底面的四个顶点恰好是下层正方体上底面各边的中点.已知最底层正方体的棱长为8,且该塔形几何体的全面积(含最底层正方体的底面面积)超过639,则该塔形中正方体的个数至少是________个.
有一塔形几何体由若干个正方体构成,构成方式如图所示:上层正方体底面的四个顶点恰好是下层正方体上底面各边的中点.已知最底层正方体的棱长为8,且该塔形几何体的全面积(含最底层正方体的底面面积)超过639,则该塔形中正方体的个数至少是________个.科目:czsx 来源:2009年浙江省杭州市萧山区中考模拟数学试卷(义蓬二中 项国庆)(解析版) 题型:填空题
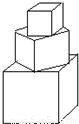
科目:czsx 来源:2009年浙江省杭州市萧山区义蓬二中中考模拟数学试卷(解析版) 题型:填空题
科目:gzsx 来源: 题型:单选题
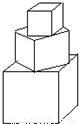
 有一塔形几何体由若干个正方体构成,构成方式如图所示,上层正方体下底面的四个顶点是下层正方体上底面各边的中点.已知最底层正方体的棱长为2,且该塔形的表面积(含最底层正方体的底面面积)超过39,则该塔形中正方体的个数至少是
有一塔形几何体由若干个正方体构成,构成方式如图所示,上层正方体下底面的四个顶点是下层正方体上底面各边的中点.已知最底层正方体的棱长为2,且该塔形的表面积(含最底层正方体的底面面积)超过39,则该塔形中正方体的个数至少是科目:gzsx 来源:2010-2011学年安徽省蚌埠二中高一(下)期中数学试卷(解析版) 题型:选择题

科目:gzsx 来源:2005年重庆市高考数学试卷(文科)(解析版) 题型:选择题

科目:gzsx 来源:江苏省高考数学一轮复习单元试卷06:等差数列与等比数列(解析版) 题型:选择题

科目:gzsx 来源:不详 题型:填空题
