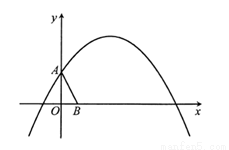
科目:czsx 来源:2014-2015学年江苏省盐城市盐都区九年级上学期期末考试数学试卷(解析版) 题型:解答题
(本题满分12分)如图,二次函数 的图像与x轴交于点A,B.点M、N在x轴上,点N在点M右侧,MN=2.以MN为直角边向上作等腰直角三角形CMN,∠CMN=90°.设点M的横坐标为m.
的图像与x轴交于点A,B.点M、N在x轴上,点N在点M右侧,MN=2.以MN为直角边向上作等腰直角三角形CMN,∠CMN=90°.设点M的横坐标为m.

(1)当点C在这条抛物线上时,求m的值.
(2)将线段CN绕点N逆时针旋转90°后,得到对应线段DN.
①当点D在这条抛物线的对称轴上时,求点D的坐标.
②以DN为直角边作等腰直角三角形DNE,当点E在这条抛物线的对称轴上时,求m的值.
科目:czsx 来源: 题型:
二次函数![]() 的图像与x轴交于B、C两点,点D是线段BC的中点,在x轴上方的A点为抛物线上的动点,连结A
的图像与x轴交于B、C两点,点D是线段BC的中点,在x轴上方的A点为抛物线上的动点,连结A![]() D,设AD=m,当∠BAC为锐角时,m的取值范围
D,设AD=m,当∠BAC为锐角时,m的取值范围 ![]() 。
。
科目:czsx 来源: 题型:
已知二次函数![]() 的图像与x轴交于B(-2,0),C(4,0)两点,点E是对称轴
的图像与x轴交于B(-2,0),C(4,0)两点,点E是对称轴![]() 与
与![]() 的交点.
的交点.
(1)求二次函数的解析表达式;
(2)T为对称轴![]() 上一动点,以点B为圆心,BT为半径作⊙B,写出直线CT与⊙B相切时,T点的坐标;
上一动点,以点B为圆心,BT为半径作⊙B,写出直线CT与⊙B相切时,T点的坐标;
(3)若在x轴上方的P点为抛物线上的动点,且∠BPC为锐角,直接写出PE的取值范围.
(4)对于(1)中得到的关系式,若![]() 为整数,在使得
为整数,在使得![]() 为完全平方数的所有
为完全平方数的所有![]() 的值中,设
的值中,设![]() 的最大值为
的最大值为![]() ,最小值为
,最小值为![]() ,次小值为
,次小值为![]() ,(注:一个数如果是另一个整数的完全平方,那么就称这个数为完全平方数.)求
,(注:一个数如果是另一个整数的完全平方,那么就称这个数为完全平方数.)求![]() 的值.
的值.
 | |||
| |||
科目:czsx 来源: 题型:
已知二次函数![]() 的图像与x轴交于B(-2,0),C(4,0)两点,点E是对称轴
的图像与x轴交于B(-2,0),C(4,0)两点,点E是对称轴![]() 与
与![]() 的交点.
的交点.
(1)求二次函数的解析表达式;
(2)T为对称轴![]() 上一动点,以点B为圆心,BT为半径作⊙B,写出直线CT与⊙B相切时,T点的坐标;
上一动点,以点B为圆心,BT为半径作⊙B,写出直线CT与⊙B相切时,T点的坐标;
(3)若在x轴上方的P点为抛物线上的动点,且∠BPC为锐角,直接写出PE的取值范围.
(4)对于(1)中得到的关系式,若![]() 为整数,在使得
为整数,在使得![]() 为完全平方数的所有
为完全平方数的所有![]() 的值中,设
的值中,设![]() 的最大值为
的最大值为![]() ,最小值为
,最小值为![]() ,次小值为
,次小值为![]() ,(注:一个数如果是另一个整数的完全平方,那么就称这个数为完全平方数.)求
,(注:一个数如果是另一个整数的完全平方,那么就称这个数为完全平方数.)求![]() 的值.
的值.
 | |||
| |||
科目:czsx 来源: 题型:
如图1,二次函数y=ax2+bx+c(a≠0)的图像与x轴交于点A、点B,与y轴交于点C,且A、B两点的坐标分别是(4,0)、(0,-2),tan∠BCO=![]() (1)求抛物线解析式;(2)点M为抛物线上一点,若以MB为直径的圆与直线BC相切于点B,求点M的坐标;(3) 如图2,若点P是抛物线上的动点,点Q是直线y=-x的动点,是否存在以点P、Q、C、O为顶点且以OC为一边的四边形是直角梯形;如果存在,请求出点P的坐标,如果不存在,请说明理由.
(1)求抛物线解析式;(2)点M为抛物线上一点,若以MB为直径的圆与直线BC相切于点B,求点M的坐标;(3) 如图2,若点P是抛物线上的动点,点Q是直线y=-x的动点,是否存在以点P、Q、C、O为顶点且以OC为一边的四边形是直角梯形;如果存在,请求出点P的坐标,如果不存在,请说明理由.
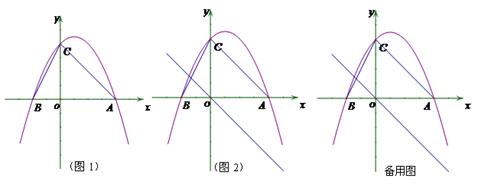
【解析】(1)利用A、B两点的坐标和tan∠BCO=![]() 求抛物线解析式
求抛物线解析式
(2)设点m(x,y),则由以MB为直径的圆与直线BC相切于点B,说明了点B为直径的一个端点,另外,BC直线方程为y=2x+4,利用BM的中点就是圆心坐标,BM垂直于CB,因此联立方程组可得M的坐标
(3)假设存在以点P、Q、C、O为顶点且以OC为一边的四边形是直角梯形
则有几种情况的一种直角为C,直角为P,直角为O,直角为Q的情况,那么分情况讨论求解,利用一组对边平行,一个角为直角,进行求解
科目:czsx 来源:2011-2012学年江苏省泰州市靖江外国语学校中考二模数学卷(解析版) 题型:解答题
如图1,二次函数y=ax2+bx+c(a≠0)的图像与x轴交于点A、点B,与y轴交于点C,且A、B两点的坐标分别是(4,0)、(0,-2),tan∠BCO= (1)求抛物线解析式;(2)点M为抛物线上一点,若以MB为直径的圆与直线BC相切于点B,求点M的坐标;(3) 如图2,若点P是抛物线上的动点,点Q是直线y=-x的动点,是否存在以点P、Q、C、O为顶点且以OC为一边的四边形是直角梯形;如果存在,请求出点P的坐标,如果不存在,请说明理由.
(1)求抛物线解析式;(2)点M为抛物线上一点,若以MB为直径的圆与直线BC相切于点B,求点M的坐标;(3) 如图2,若点P是抛物线上的动点,点Q是直线y=-x的动点,是否存在以点P、Q、C、O为顶点且以OC为一边的四边形是直角梯形;如果存在,请求出点P的坐标,如果不存在,请说明理由.

【解析】(1)利用A、B两点的坐标和tan∠BCO= 求抛物线解析式
求抛物线解析式
(2)设点m(x,y),则由以MB为直径的圆与直线BC相切于点B,说明了点B为直径的一个端点,另外,BC直线方程为y=2x+4,利用BM的中点就是圆心坐标,BM垂直于CB,因此联立方程组可得M的坐标
(3)假设存在以点P、Q、C、O为顶点且以OC为一边的四边形是直角梯形
则有几种情况的一种直角为C,直角为P,直角为O,直角为Q的情况 ,那么分情况讨论求解,利用一组对边平行,一个角为直角,进行求解
科目:czsx 来源: 题型:
如图,已知二次函数y=ax2+bx+8(a≠0)的图像与x轴交于点A(-2,0),B,
与y轴交于点C,tan∠ABC=2.
(1)求抛物线的解析式及其顶点D的坐标;
(2)设直线CD交x轴于点E.在线段OB的垂直平分线上是否存在点P,使得经过点P的直线PM垂直于直线CD,且与直线OP的夹角为75°?若存在,求出点P的坐标;若不存在,请说明理由;
(3)过点B作x轴的垂线,交直线CD于点F,将抛物线沿其对称轴向上平移,使抛物线与线段EF总有公共点.试探究:抛物线最多可以向上平移多少个单位长度?
科目:czsx 来源: 题型:
如图,已知二次函数y=ax2+bx+8(a≠0)的图像与x轴交于点A(-2,0),B,与y轴交于点C,tan∠ABC=2.
(1)求抛物线的解析式及其顶点D的坐标;
(2)设直线CD交x轴于点E.在线段OB的垂直平分线上是否存在点P,使得经过点P的直线PM垂直于直线CD,且与直线OP的夹角为75°?若存在,求出点P的坐标;若不存在,请说明理由;
(3)过点B作x轴的垂线,交直线CD于点F,将抛物线沿其对称轴向上平移,使抛物线与线段EF总有公共点.试探究:抛物线最多可以向上平移多少个单位长度?
科目:czsx 来源: 题型:

科目:czsx 来源:2010-2011学年甘肃省白银市五合中学初一第一学期期末试卷数学试题 题型:解答题
如图,已知二次函数y=ax2+bx+8(a≠0)的图像与x轴交于点A(-2,0),B,与y轴交于点C,tan∠ABC=2.
(1)求抛物线的解析式及其顶点D的坐标;
(2)设直线CD交x轴于点E.在线段OB的垂直平分线上是否存在点P,使得经过点P的直线PM垂直于直线CD,且与直线OP的夹角为75°?若存在,求出点P的坐标;若不存在,请说明理由;
(3)过点B作x轴的垂线,交直线CD于点F,将抛物线沿其对称轴向上平移,使抛物线与线段EF总有公共点.试探究:抛物线最多可以向上平移多少个单位长度?
科目:czsx 来源:2011届北京市东城区中考一模数学试卷 题型:解答题
如图,已知二次函数y=ax2+bx+8(a≠0)的图像与x轴交于点A(-2,0),B,
与y轴交于点C,tan∠ABC=2.
(1)求抛物线的解析式及其顶点D的坐标;
(2)设直线CD交x轴于点E.在线段OB的垂直平分线上是否存在点P,使得经过点P的直线PM垂直于直线CD,且与直线OP的夹角为75°?若存在,求出点P的坐标;若不存在,请说明理由;
(3)过点B作x轴的垂线,交直线CD于点F,将抛物线沿其对称轴向上平移 ,使抛物线与线段EF总有公共点.试探究:抛物线最多可以向上平移多少个单位长度?
,使抛物线与线段EF总有公共点.试探究:抛物线最多可以向上平移多少个单位长度?
科目:czsx 来源:2010-2011学年北京市考一模数学试卷 题型:解答题
如图,已知二次函数y=ax2+bx+8(a≠0)的图像与x轴交于点A(-2,0),B,
与y轴交于点C,tan∠ABC=2.
(1)求抛物线的解析式及其顶点D的坐标;
(2)设直线CD交x轴于点E.在线段OB的垂直平分线上是否存在点P,使得经过点P的直线PM垂直于直线CD,且与直线OP的夹角为75°?若存在,求出点P的坐标;若不存在,请说明理由;
(3)过点B作x轴的垂线,交直线CD于点F,将抛物线沿其对称轴向上平移,使抛物线与线段EF总有公共点.试探究:抛物线最多可以向上平移多少个单位长度?

科目:czsx 来源:2013届甘肃省白银市初一第一学期期末试卷数学试题 题型:解答题
如图,已知二次函数y=ax2+bx+8(a≠0)的图像与x轴交于点A(-2,0),B,与y轴交于点C,tan∠ABC=2.

(1)求抛物线的解析式及其顶点D的坐标;
(2)设直线CD交x轴于点E.在线段OB的垂直平分线上是否存在点P,使得经过点P的直线PM垂直于直线CD,且与直线OP的夹角为75°?若存在,求出点P的坐标;若不存在,请说明理由;
(3)过点B作x轴的垂线,交直线CD于点F,将抛物线沿其对称轴向上平移,使抛物线与线段EF总有公共点.试探究:抛物线最多可以向上平移多少个单位长度?
科目:czsx 来源:数学教研室 题型:044
(1)求证:不论m取何实数,这个二次函数的图像与x轴必有两个交点;
(2)设这个二次函数的图像与x轴交于点A(x1,0)、B(x2,0),且x1、x2的倒数和为![]() ,求这个二次函数的解析式。
,求这个二次函数的解析式。
科目:czsx 来源:解题升级 解题快速反应一典通 九年级级数学 题型:044
已知二次函数y=x2-2(m-1)x+m2-2m-3,其中m为实数.
(1)求证不论m取何实数,这个二次函数的图像与x轴必有两个交点;
(2)设这个二次函数的图像与x轴交于点A(x1,0)B(x2,0),且x1、x2的倒数和为![]() ,求这个二次函数的解析式.
,求这个二次函数的解析式.
科目:czsx 来源:浙江省杭州市城北片2012届九年级上学期期中质量检测数学试题 题型:022
二次函数y=x2+2x+3的图像与x轴交于B、C两点,点D是线段BC的中点,在x轴上方的A点为抛物线上的动点,连结AD,设AD=m,当∠BAC为锐角时,m的取值范围
_________.科目:czsx 来源: 题型:
已知二次函数y=x2+bx+c的图像与x轴交于A、B两点,AB=4,其中点A的坐标为(1,0).
(1)求二次函数的关系式及顶点坐标;
(2)请设计一种平移方法,使(1)中的二次函数图像的顶点在一次函数y=x的图像上,并直接写出平移后相应的二次函数的关系式.
科目:czsx 来源:中考数学专项练习 题型:044
设二次函数y=-![]() +(m-2)x+3(m+1)的图像与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,线段OA与OB的长的积等于6(O为坐标原点),连结AC、BC,求sinC的值.
+(m-2)x+3(m+1)的图像与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,线段OA与OB的长的积等于6(O为坐标原点),连结AC、BC,求sinC的值.
科目:czsx 来源: 题型:
如图,已知二次函数 (其中0<m<1)的图像与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴为直线l.设P为对称轴l上的点,连接PA、PC,PA=PC.
(其中0<m<1)的图像与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴为直线l.设P为对称轴l上的点,连接PA、PC,PA=PC.
(1)∠ABC的度数为 °;
(2)求P点坐标(用含m的代数式表示);
(3)在坐标轴上是否存在点Q(与原点O不重合),使得以Q、B、C为顶点的三角形与△PAC相似,且线段PQ的长度最小?如果存在,求出所有满足条件的点Q的坐标;如果不存在,请说明理由.

科目:czsx 来源:2017届江苏省苏州市相城区九年级上学期期末考试数学试卷(解析版) 题型:判断题
如图,二次函数 的图像与
的图像与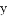 轴交于点
轴交于点 ,点
,点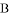 是
是 轴上一点,其坐标为(1,0),连接
轴上一点,其坐标为(1,0),连接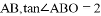 .
.
(1)则点 的坐标为 ,
的坐标为 ,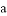 = ;
= ;
(2)过点 作
作 的垂线与该二次函数的图像交于另一点
的垂线与该二次函数的图像交于另一点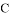 ,求点
,求点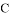 的坐标;
的坐标;
(3)连接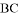 ,过点
,过点 作直线
作直线 交线段
交线段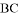 于点
于点 ,设点
,设点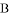 、点
、点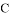 到
到 的距离分别为
的距离分别为 、
、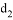 ,求
,求 的最大值.
的最大值.