判断抛物线的顶点D与以BC为直径的的圆M的位置关系答案解析
科目:czsx
来源:不详
题型:解答题
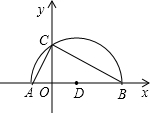
如图(1),直线

与x轴交于点A、与y轴交于点D,以AD为腰,以x轴为底作等腰梯形ABCD(AB>CD),且等腰梯形的面积是8

,抛物线经过等腰梯形的四个顶点.

图(1)
(1) 求抛物线的解析式;
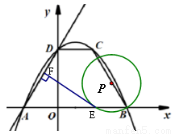
(2) 如图(2)若点P为BC上的—个动点(与B、C不重合),以P为圆心,BP长为半径作圆,与

轴的另一个交点为E,作EF⊥AD,垂足为F,请判断EF与⊙P的位置关系,并给以证明;

图(2)
(3) 在(2)的条件下,是否存在点P,使⊙P与y轴相切,如果存在,请求出点P的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:2013-2014学年广东省深圳市九年级3月联考数学试卷(解析版)
题型:解答题
如图(1),直线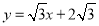 与x轴交于点A、与y轴交于点D,以AD为腰,以x轴为底作等腰梯形ABCD(AB>CD),且等腰梯形的面积是8
与x轴交于点A、与y轴交于点D,以AD为腰,以x轴为底作等腰梯形ABCD(AB>CD),且等腰梯形的面积是8 ,抛物线经过等腰梯形的四个顶点.
,抛物线经过等腰梯形的四个顶点.

图(1)
(1) 求抛物线的解析式;
(2) 如图(2)若点P为BC上的—个动点(与B、C不重合),以P为圆心,BP长为半径作圆,与 轴的另一个交点为E,作EF⊥AD,垂足为F,请判断EF与⊙P的位置关系,并给以证明;
轴的另一个交点为E,作EF⊥AD,垂足为F,请判断EF与⊙P的位置关系,并给以证明;
图(2)
(3) 在(2)的条件下,是否存在点P,使⊙P与y轴相切,如果存在,请求出点P的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
7.如图,抛物线y=-$\frac{1}{2}$x
2+mx+n与x轴交于A,B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,顶点为P点,已知A(-1,0),B(4,0).
(1)求抛物线的表达式;
(2)试判断以点P为圆心,PC为半径的圆与直线CD的位置关系并说明理由;
(3)点E是线段BC上的一动点.
①是否存在这样的点E,使△ECD是等腰三角形,如果存在,直接写出E点的坐标,如果不存在,请说明理由;
②过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时E点的坐标.

查看答案和解析>>
科目:czsx
来源:
题型:解答题
已知二次函数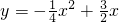 的图象如图所示.
的图象如图所示.
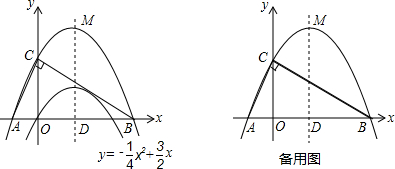
(1)求它的对称轴与x轴交点D的坐标;
(2)将该抛物线沿它的对称轴向上平移k个单位,设平移后的抛物线与x轴,y轴的交点分别为A、B、C三点,若∠ACB=90°,求此时抛物线的解析式;
(3)设(2)中平移后的抛物线的顶点为M,以AB为直径,D为圆心作⊙D,试判断直线CM与⊙D的位置关系,并说明理由.
(4)在(2)的条件下,平行于x轴的直线x=t(0<t<k) 分别交AC、BC于E、F两点,试问在x轴上是否存在点P,使得△PEF是等腰直角三角形?若存在,请直接写P点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
如图(1),直线
y=x+2与x轴交于点A、与y轴交于点D,以AD为腰,以x轴为底作等腰梯形ABCD(AB>CD),且等腰梯形的面积是8
,抛物线经过等腰梯形的四个顶点.

(1)求抛物线的解析式;
(2)如图(2)若点P为BC上的-个动点(与B、C不重合),以P为圆心,BP长为半径作圆,与x轴的另一个交点为E,作EF⊥AD,垂足为F,请判断EF与⊙P的位置关系,并给以证明;
(3)在(2)的条件下,是否存在点P,使⊙P与y轴相切?如果存在,请求出点P的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
 已知二次函数
已知二次函数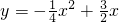 .
.
(1)求它的对称轴与x轴交点D的坐标;
(2)将该抛物线沿它的对称轴向上平移,如图所示,设平移后的抛物线的顶点为M,与x轴、y轴的交点分别为A、B、C三点,连接AC、BC,若∠ACB=90°.
①求此时抛物线的解析式;
②以AB为直径作圆,试判断直线CM与此圆的位置关系,并说明理由.
查看答案和解析>>
科目:czsx
来源:2011-2012学年北京市大兴区九年级(上)期末数学试卷(解析版)
题型:解答题
已知二次函数
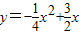
.
(1)求它的对称轴与x轴交点D的坐标;
(2)将该抛物线沿它的对称轴向上平移,如图所示,设平移后的抛物线的顶点为M,与x轴、y轴的交点分别为A、B、C三点,连接AC、BC,若∠ACB=90°.
①求此时抛物线的解析式;
②以AB为直径作圆,试判断直线CM与此圆的位置关系,并说明理由.
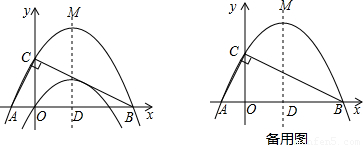
查看答案和解析>>
科目:czsx
来源:
题型:
已知二次函数
y=-x2+x的图象如图所示.
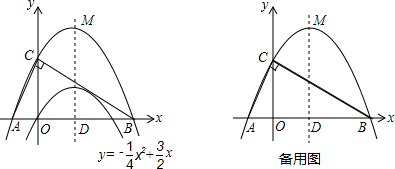
(1)求它的对称轴与x轴交点D的坐标;
(2)将该抛物线沿它的对称轴向上平移k个单位,设平移后的抛物线与x轴,y轴的交点分别为A、B、C三点,若∠ACB=90°,求此时抛物线的解析式;
(3)设(2)中平移后的抛物线的顶点为M,以AB为直径,D为圆心作⊙D,试判断直线CM与⊙D的位置关系,并说明理由.
(4)在(2)的条件下,平行于x轴的直线x=t(0<t<k) 分别交AC、BC于E、F两点,试问在x轴上是否存在点P,使得△PEF是等腰直角三角形?若存在,请直接写P点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:不详
题型:解答题
已知二次函数
y=-x2+x的图象如图所示.

(1)求它的对称轴与x轴交点D的坐标;
(2)将该抛物线沿它的对称轴向上平移k个单位,设平移后的抛物线与x轴,y轴的交点分别为A、B、C三点,若∠ACB=90°,求此时抛物线的解析式;
(3)设(2)中平移后的抛物线的顶点为M,以AB为直径,D为圆心作⊙D,试判断直线CM与⊙D的位置关系,并说明理由.
(4)在(2)的条件下,平行于x轴的直线x=t(0<t<k)分别交AC、BC于E、F两点,试问在x轴上是否存在点P,使得△PEF是等腰直角三角形?若存在,请直接写P点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
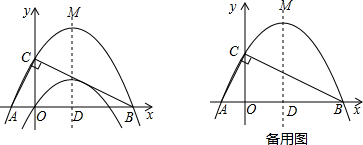
已知二次函数
y=-x2+x.
(1)求它的对称轴与x轴交点D的坐标;
(2)将该抛物线沿它的对称轴向上平移,如图所示,设平移后的抛物线的顶点为M,与x轴、y轴的交点分别为A、B、C三点,连接AC、BC,若∠ACB=90°.
①求此时抛物线的解析式;
②以AB为直径作圆,试判断直线CM与此圆的位置关系,并说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
如图:在平面直角坐标系xOy中,矩形OABC的边OA在x轴上,顶点B(4,2)在抛物线y
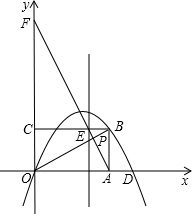
=ax
2+bx上,且抛物线交x轴于另一点D(6,0),抛物线的对称轴交BC边于E,直线AE分别交y轴于F、交OB于P.
(1)求抛物线对应的二次函数解析式;
(2)若以点O为圆心,OP为半径作⊙O,试判断AE与⊙O的位置关系,并说明理由;
(3)若动直线MN⊥x轴于N交抛物线于M,且在y轴的右侧运动,是否存在点M使得△AMN与△ABP相似?若存在,请求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
如图:在平面直角坐标系xOy中,矩形OABC的边OA在x轴上,顶点B(4,2)在抛物线y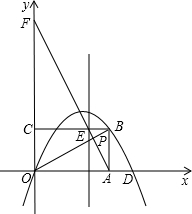 =ax2+bx上,且抛物线交x轴于另一点D(6,0),抛物线的对称轴交BC边于E,直线AE分别交y轴于F、交OB于P.
=ax2+bx上,且抛物线交x轴于另一点D(6,0),抛物线的对称轴交BC边于E,直线AE分别交y轴于F、交OB于P.
(1)求抛物线对应的二次函数解析式;
(2)若以点O为圆心,OP为半径作⊙O,试判断AE与⊙O的位置关系,并说明理由;
(3)若动直线MN⊥x轴于N交抛物线于M,且在y轴的右侧运动,是否存在点M使得△AMN与△ABP相似?若存在,请求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:福建省期中题
题型:解答题
如图:在平面直角坐标系xOy中,矩形OABC的边OA在x轴上,顶点B(4,2)在抛物线上,且抛物线交x轴于另一点D(6,0),抛物线的对称轴交BC边于E,直线AE分别交y轴于F、交OB于P。
(1)求抛物线对应的二次函数解析式;
(2)若以点O为圆心,OP为半径作⊙O,试判断AE与⊙O的位置关系,并说明理由;
(3)若动直线MN⊥x轴于N交抛物线于M,且在y轴的右侧运动,是否存在点M使得△AMN与△ABP相似?若存在请求出点M的坐标;若不存在,请说明理由。
查看答案和解析>>
科目:czsx
来源:
题型:
如图:在平面直角坐标系xOy中,矩形OABC的边OA在x轴上,顶点B(4,2)在抛物线 上,且抛物线交x轴于另一点D(6,0),抛物线的对称轴交BC边于E,直线AE分别交y轴于F、交OB于P。
上,且抛物线交x轴于另一点D(6,0),抛物线的对称轴交BC边于E,直线AE分别交y轴于F、交OB于P。
(1)求抛物线对应的二次函数解析式;
(2)若以点O为圆心,OP为半径作⊙O,试判断AE与⊙O的位置关系,并说明理由;
(3)若动直线MN⊥x轴于N交抛物线于M,且在y轴的右侧运动,是否存在点M使得△AMN与△ABP相似?若存在请求出点M的坐标;若不存在,请说明理由。

查看答案和解析>>
科目:czsx
来源:
题型:
已知:如图,平面直角坐标系中,半圆的直径AB在x轴上,圆心为D.半圆交y轴于点C,AC=2
,
BC=4
.
(1)证明:△AOC∽△ACB;
(2)求以AO、BO两线段长为根的一元二次方程;
(3)求图象经过A、B、C三点的二次函数的表达式;
(4)设此抛物线的顶点为E,连接EC,试判断直线EC与⊙O的位置关系,并说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
已知:如图,平面直角坐标系中,半圆的直径AB在x轴上,圆心为D.半圆交y轴于点C,AC=2 ,
,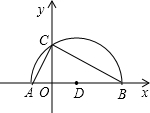 BC=4
BC=4 .
.
(1)证明:△AOC∽△ACB;
(2)求以AO、BO两线段长为根的一元二次方程;
(3)求图象经过A、B、C三点的二次函数的表达式;
(4)设此抛物线的顶点为E,连接EC,试判断直线EC与⊙O的位置关系,并说明理由.
查看答案和解析>>
科目:czsx
来源:《3.4-3.6 圆》2010年同步训练(B卷)(解析版)
题型:解答题
已知:如图,平面直角坐标系中,半圆的直径AB在x轴上,圆心为D.半圆交y轴于点C,AC=2
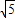
,BC=4
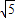
.
(1)证明:△AOC∽△ACB;
(2)求以AO、BO两线段长为根的一元二次方程;
(3)求图象经过A、B、C三点的二次函数的表达式;
(4)设此抛物线的顶点为E,连接EC,试判断直线EC与⊙O的位置关系,并说明理由.
查看答案和解析>>
科目:czsx
来源:2008-2009学年安徽省淮北市五校联考九年级(上)期末数学试卷(解析版)
题型:解答题
已知:如图,平面直角坐标系中,半圆的直径AB在x轴上,圆心为D.半圆交y轴于点C,AC=2
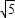
,BC=4

.
(1)证明:△AOC∽△ACB;
(2)求以AO、BO两线段长为根的一元二次方程;
(3)求图象经过A、B、C三点的二次函数的表达式;
(4)设此抛物线的顶点为E,连接EC,试判断直线EC与⊙O的位置关系,并说明理由.

查看答案和解析>>

 与x轴交于点A、与y轴交于点D,以AD为腰,以x轴为底作等腰梯形ABCD(AB>CD),且等腰梯形的面积是8
与x轴交于点A、与y轴交于点D,以AD为腰,以x轴为底作等腰梯形ABCD(AB>CD),且等腰梯形的面积是8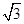 ,抛物线经过等腰梯形的四个顶点.
,抛物线经过等腰梯形的四个顶点.
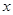 轴的另一个交点为E,作EF⊥AD,垂足为F,请判断EF与⊙P的位置关系,并给以证明;
轴的另一个交点为E,作EF⊥AD,垂足为F,请判断EF与⊙P的位置关系,并给以证明;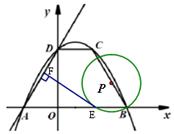
 与x轴交于点A、与y轴交于点D,以AD为腰,以x轴为底作等腰梯形ABCD(AB>CD),且等腰梯形的面积是8
与x轴交于点A、与y轴交于点D,以AD为腰,以x轴为底作等腰梯形ABCD(AB>CD),且等腰梯形的面积是8 ,抛物线经过等腰梯形的四个顶点.
,抛物线经过等腰梯形的四个顶点.
 轴的另一个交点为E,作EF⊥AD,垂足为F,请判断EF与⊙P的位置关系,并给以证明;
轴的另一个交点为E,作EF⊥AD,垂足为F,请判断EF与⊙P的位置关系,并给以证明;
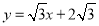 与x轴交于点A、与y轴交于点D,以AD为腰,以x轴为底作等腰梯形ABCD(AB>CD),且等腰梯形的面积是8
与x轴交于点A、与y轴交于点D,以AD为腰,以x轴为底作等腰梯形ABCD(AB>CD),且等腰梯形的面积是8 ,抛物线经过等腰梯形的四个顶点.
,抛物线经过等腰梯形的四个顶点.
 轴的另一个交点为E,作EF⊥AD,垂足为F,请判断EF与⊙P的位置关系,并给以证明;
轴的另一个交点为E,作EF⊥AD,垂足为F,请判断EF与⊙P的位置关系,并给以证明;

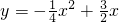 的图象如图所示.
的图象如图所示.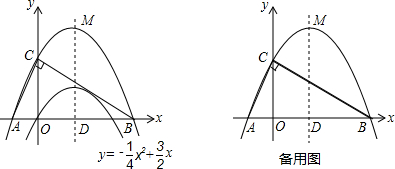

 已知二次函数
已知二次函数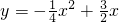 .
.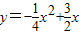 .
.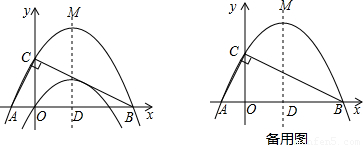
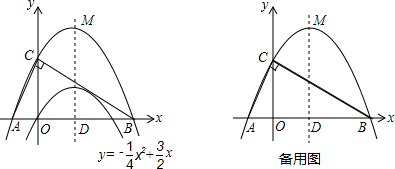

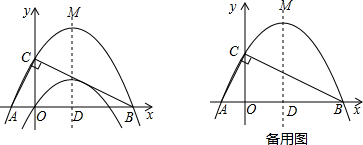 已知二次函数y=-
已知二次函数y=- =ax2+bx上,且抛物线交x轴于另一点D(6,0),抛物线的对称轴交BC边于E,直线AE分别交y轴于F、交OB于P.
=ax2+bx上,且抛物线交x轴于另一点D(6,0),抛物线的对称轴交BC边于E,直线AE分别交y轴于F、交OB于P. =ax2+bx上,且抛物线交x轴于另一点D(6,0),抛物线的对称轴交BC边于E,直线AE分别交y轴于F、交OB于P.
=ax2+bx上,且抛物线交x轴于另一点D(6,0),抛物线的对称轴交BC边于E,直线AE分别交y轴于F、交OB于P.
![]() 上,且抛物线交x轴于另一点D(6,0),抛物线的对称轴交BC边于E,直线AE分别交y轴于F、交OB于P。
上,且抛物线交x轴于另一点D(6,0),抛物线的对称轴交BC边于E,直线AE分别交y轴于F、交OB于P。
 BC=4
BC=4 ,
, BC=4
BC=4 .
.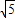 ,BC=4
,BC=4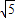 .
.
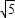 ,BC=4
,BC=4 .
.