
如图(1),直线 与x轴交于点A、与y轴交于点D,以AD为腰,以x轴为底作等腰梯形ABCD(AB>CD),且等腰梯形的面积是8
与x轴交于点A、与y轴交于点D,以AD为腰,以x轴为底作等腰梯形ABCD(AB>CD),且等腰梯形的面积是8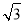 ,抛物线经过等腰梯形的四个顶点.
,抛物线经过等腰梯形的四个顶点.

图(1)
(1) 求抛物线的解析式;
(2) 如图(2)若点P为BC上的—个动点(与B、C不重合),以P为圆心,BP长为半径作圆,与 轴的另一个交点为E,作EF⊥AD,垂足为F,请判断EF与⊙P的位置关系,并给以证明;
轴的另一个交点为E,作EF⊥AD,垂足为F,请判断EF与⊙P的位置关系,并给以证明;

图(2)
(3) 在(2)的条件下,是否存在点P,使⊙P与y轴相切,如果存在,请求出点P的坐标;如果不存在,请说明理由.
(1) ;(2)EF与⊙P相切.,证明见解析;(3) 存在, x=
;(2)EF与⊙P相切.,证明见解析;(3) 存在, x=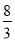 ,P(
,P(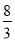 ,
,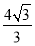 ).
).
【解析】
试题分析:(1)过C作CE⊥AB于E,利用矩形的性质分别求得三点的坐标,利用求得的点的坐标,用待定系数法求得二次函数的解析式即可;
(2)连结PE,可以得到:PE∥DA,从而得出EF与⊙P相切;
(3)设⊙P与y轴相切于点G,P作PQ⊥x轴于点Q,设Q(x,0),用含有x的代数式分别表示出PG和PB,再根据PG=PB求出x的值即可.
试题解析:(1) ∵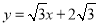 ,当x=0时, y=
,当x=0时, y=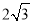 ;当y=0时,x=-2,
;当y=0时,x=-2,
∴A(-2,0),D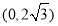 ,
,
∵ABCD为等腰梯形,
∴AD=BC,∠OAD=∠OBC
过点C作CH⊥AB于点H,则AO=BH,OH=DC.

∵ABCD的面积是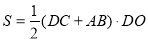 ,
,
∴8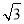 =
=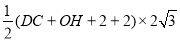 ,
,
∴DC=2,
∴C(2, 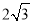 ),B(4,0),
),B(4,0),
设抛物线解析式为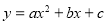 (
(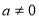 ),代入A(-2,0),D
),代入A(-2,0),D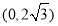 ,B(4,0)
,B(4,0)
得 ,
,
解得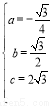 ,
,
即 ;
;
(2)连结PE,∵PE=PB,
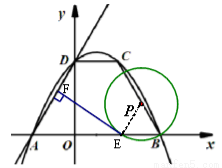
∴∠PBE=∠PEB,
∵∠PBE=∠DAB,
∴∠DAB=∠PBE,
∴PE∥DA,
∵EF⊥AD,
∴∠FEP=∠AFF=90°,
又PE为半径,EF与⊙P相切.;
(3)设⊙P与y轴相切于点G,P作PQ⊥x轴于点Q,
设Q(x,0),则QB=4-x,
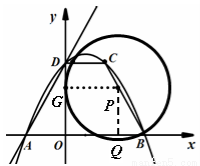
∵∠PBA=∠DAO,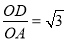 ,
,
∴∠PBA=∠DAO=60°,
∴PQ=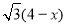 , PB=8-2x ,P(x,
, PB=8-2x ,P(x, 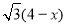 ),
),
∵⊙P与y轴相切于点G,⊙P过点B,
∴PG=PB,
∴x=8-2x,
∴x=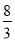 ,P(
,P(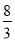 ,
,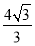 ).
).
考点:二次函数综合题.


 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案科目:初中数学 来源:2013-2014学年新人教版初中数学浙江永嘉桥下瓯渠中学中考总复习三十二讲练习卷(解析版) 题型:选择题
如下图,A、B、C三点在正方形网格线的交点处,若将△ACB绕着点A逆时针旋转得到△AC′B′,则tan B′的值为( )
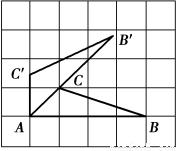
A. B.
B.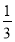 C.
C.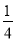 D.
D.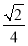
查看答案和解析>>
科目:初中数学 来源:2013-2014学年新人教版初中数学浙江永嘉桥下瓯渠中学中考总复习三十一讲练习卷(解析版) 题型:选择题
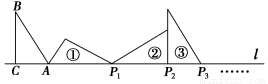
如图Rt△ABC中,∠ACB=90°,∠B=30°,AC=1,且AC在直线l上,将△ABC绕点A顺时针旋转到①,可得到点P1,此时AP1=2;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时AP2=2+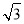 ;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=3+
;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=3+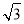 ;…按此规律继续旋转,直到点P2012为止,则AP2012等于( )
;…按此规律继续旋转,直到点P2012为止,则AP2012等于( )
A.2 011+671 B.2 012+671
B.2 012+671
C.2 013+671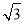 D.2 014+671
D.2 014+671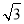
查看答案和解析>>
科目:初中数学 来源:2013-2014学年广东省深圳市石岩公学九年级3月质量检测数学试卷(解析版) 题型:选择题
已知数据5,3,5,4,6,5,4,下列说法正确的是( )
A. 中位数是4 B. 众数是4
C. 中位数与众数都是5 D. 中位数与平均数都是5。
查看答案和解析>>
科目:初中数学 来源:2013-2014学年广东省深圳市九年级3月联考数学试卷(解析版) 题型:选择题
有A、B两枚均匀的小立方体(立方体的每个面上分别标有数字1,2,3,4,5,6),以小莉掷A立方体朝上的数字为x、小明掷B立方体朝上的数字为y来确定点P(x,y),那么他们各掷一次所确定的点P落在抛物线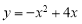 上的概率为( )
上的概率为( )
A.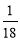 B.
B.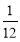 C.
C.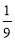 D.
D.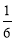
查看答案和解析>>
科目:初中数学 来源:2013-2014学年广东省九年级下册期末检测数学试卷(解析版) 题型:解答题
如右图在某建筑物AC上,挂着“和谐广东”的宣传条幅BC,小明站在点F处,看条幅顶端B,测的仰角为 ,条幅方向前行20米到达点E处,看到条幅顶端B,测的仰角为
,条幅方向前行20米到达点E处,看到条幅顶端B,测的仰角为 ,求宣传条幅再往BC的长,(小明的身高不计,结果精确到0.1米)
,求宣传条幅再往BC的长,(小明的身高不计,结果精确到0.1米)

查看答案和解析>>
科目:初中数学 来源:2013-2014学年广东省中考预测二数学试卷(解析版) 题型:解答题
阅读下面的例题,并回答问题.
【例题】解一元二次不等式:x2-2x-8>0.
【解析】
对x2-2x-8分解因式,得x2-2x-8=(x-1)2-9=(x-1)2-32=(x+2)(x-4),
∴(x+2)(x-4)>0.由“两实数相乘,同号得正,异号得负”,可得 ①或
①或 ②
②
解①得x>4;解②得x<-2.
故x2-2x-8>0的解集是x>4或x<-2.
(1)直接写出x2-9>0的解是 ;
(2)仿照例题的解法解不等式:x2+4x-21<0;
(3)求分式不等式: ≤0的解集.
≤0的解集.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com