
�Ķ���������⣬���ش����⣮
�����⡿��һԪ���β���ʽ��x2-2x-8��0��
��������
��x2-2x-8�ֽ���ʽ����x2-2x-8=��x-1��2-9=��x-1��2-32=��x+2����x-4����
����x+2����x-4����0���ɡ���ʵ����ˣ�ͬ�ŵ�������ŵø������ɵ� ����
���� ��
��
������x��4��������x��-2��
��x2-2x-8��0�Ľ⼯��x��4��x��-2��
��1��ֱ��д��x2-9��0�Ľ����� ����
��2����������Ľⷨ�ⲻ��ʽ��x2+4x-21��0��
��3�����ʽ����ʽ�� ��0�Ľ⼯��
��0�Ľ⼯��
��1��x��3��x��-3����2��-7��x��3��(3) 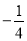 ��x��2��
��x��2��
��������
�����������1������ƽ���ʽ������ʽ�ֽ⣻
��2�����á�ʮ����˷����Բ���ʽ����߽�����ʽ�ֽ⣻
��3����Ҫ�������ۣ�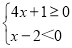 ��
��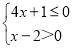 ��
��
�����������1����ԭ����ʽ��
��x+3����x-3����0
��� x��3��x��-3��
��2����������
x2+4x-21=x2+4x+4-25=��x+2��2-52=��x+7����x-3����
����x+7����x-3����0��
�ɡ���ʵ����ˣ�ͬ�ŵ�������ŵø������ɵ�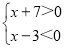 ����
����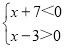 ��
��
������-7��x��3�����⣮
��x2+4x-21��0�Ľ⼯��-7��x��3��
��3����������
�ɡ���ʵ�������ͬ�ŵ�������ŵø����ҡ���ĸ����Ϊ0�����ɵ�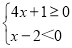 ��
��
��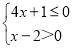 ��
��
������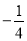 ��x��2�����⣮
��x��2�����⣮
��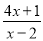 ��0�Ľ⼯��
��0�Ľ⼯��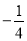 ��x��2��
��x��2��
���㣺һԪһ�β���ʽ���Ӧ�ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2013-2014ѧ��㶫ʡ�����о��꼶3��������ѧ�Ծ��������棩 ���ͣ������
��ͼ(1)��ֱ�� ��x�ύ�ڵ�A����y�ύ�ڵ�D����ADΪ������x��Ϊ������������ABCD(AB��CD)���ҵ������ε������8
��x�ύ�ڵ�A����y�ύ�ڵ�D����ADΪ������x��Ϊ������������ABCD(AB��CD)���ҵ������ε������8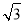 �������߾����������ε��ĸ�����.
�������߾����������ε��ĸ�����.

ͼ(1)
(1) �������ߵĽ���ʽ��
(2) ��ͼ��2������PΪBC�ϵġ������㣨��B��C���غϣ�����PΪԲ�ģ�BP��Ϊ�뾶��Բ���� �����һ������ΪE����EF��AD������ΪF�����ж�EF����P��λ�ù�ϵ��������֤����
�����һ������ΪE����EF��AD������ΪF�����ж�EF����P��λ�ù�ϵ��������֤����

ͼ��2��
(3) �ڣ�2���������£��Ƿ���ڵ�P��ʹ��P��y�����У�������ڣ��������P�����ꣻ��������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2013-2014ѧ��㶫ʡ���꼶�²���ĩ�����ѧ�Ծ��������棩 ���ͣ�ѡ����
2008�걱������ʥ����ȫ�ݵ����ԼΪ137000km���ÿ�ѧ�������ɱ�ʾΪ( )
A��1.37��103km B��137��103km C��1.37��105km D��137��105km
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2013-2014ѧ��㶫ʡ�Ƹ��о��꼶��ѧ����ĩ������ѧ�Ծ��������棩 ���ͣ�ѡ����
���һ�����εİ뾶��1��������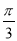 ����ô�����ε�Բ�ĽǵĴ�СΪ
����ô�����ε�Բ�ĽǵĴ�СΪ
A��30�� B��45�� C��60�� D��90��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2013-2014ѧ��㶫ʡ�Ƹ��о��꼶��ѧ����ĩ������ѧ�Ծ��������棩 ���ͣ�ѡ����
��һ���ʵؾ������������Ϸֱ����1��6�ĵ��������������ӣ���ͼ���۲����ϵ�һ��ĵ�������������Ȼ�¼�����

A�����ֵĵ���������0 B�����ֵĵ�����7
C�����ֵĵ�����2 D�����ֵĵ���Ϊ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2013-2014ѧ��㶫ʡ�п�Ԥ�����ѧ�Ծ��������棩 ���ͣ������
Ϊ����߲�Ʒ�ĸ���ֵ��ij��˾�ƻ����з�������1200���²�Ʒ���о��ӹ�����Ͷ���г������мס��������������߱��ӹ���������˾�ɳ������Ա�ֱ������乤���˽���������������Ϣ��
��Ϣһ�����������ӹ����������Ʒ���ҹ��������ӹ����������Ʒ����10�죻
��Ϣ�����ҹ���ÿ��ӹ��������Ǽ���ÿ��ӹ�������1.5����
����������Ϣ����ס�����������ÿ��ֱ��ܼӹ����ټ��²�Ʒ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2013-2014ѧ��㶫ʡ�п�Ԥ�����ѧ�Ծ��������棩 ���ͣ������
������=42�㣬����������ǵĶ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2013-2014ѧ��㶫��ͷ�о��꼶��ѧ�ڵ�һ�νο�����ѧ�Ծ��������棩 ���ͣ������
�Ȼ�������ֵ��

 ������x=
������x=
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2013-2014ѧ��ɽ��ʡ����ѧҵˮƽ������ѧģ���Ծ��������棩 ���ͣ������
��ͼ����֪������y=�� x2+bx+4��x���ཻ��A��B���㣬��y���ཻ�ڵ�C������֪A�������ΪA����2��0����
x2+bx+4��x���ཻ��A��B���㣬��y���ཻ�ڵ�C������֪A�������ΪA����2��0����
��1���������ߵĽ���ʽ�����ĶԳ��
��2�����C�����꣬����AC��BC�����߶�BC����ֱ�ߵĽ���ʽ��
��3���������ߵĶԳ������Ƿ���ڵ�Q��ʹ��ACQΪ���������Σ������ڣ��������������Q�����ꣻ�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com