
科目:czsx 来源: 题型:
A、
| ||
B、
| ||
C、
| ||
D、
|
科目:gzsx 来源: 题型:
| a2+b2 |
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 3 |
| 6 |
| 5 |
科目:gzsx 来源:河北省邯郸市临漳一中2012届高三春季开学摸底考试数学文科试题 题型:013
在平面直角坐标系中,O为原点,已知两点A(3,1),B(-1,3),若C满足![]() =α
=α![]() +β
+β![]() 其中α,β∈R且α+β=1,则点C的轨迹方程是
其中α,β∈R且α+β=1,则点C的轨迹方程是
A.3x+2y-11-0
B.(x-1)2+(y-2)2=5
C.2x-y=0
D.x+2y-5=0
科目:gzsx 来源:2012年人教A版高中数学必修四2.3平面向量基本定理及坐标表示(三)(解析版) 题型:填空题
在平面直角坐标系中,O为原点,已知两点A(1,-2),B(-1,4),若点C满足 =α
=α +β
+β ,其中0≤α≤1且α+β=1,则点C的轨迹方程为________.
,其中0≤α≤1且α+β=1,则点C的轨迹方程为________.
科目:gzsx 来源:2011-2012学年河北省高三高考预测文科数学试卷(解析版) 题型:选择题
在平面直角坐标系中,O为原点,已知两点 ,若
,若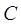 满足
满足 其中
其中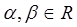 且
且 ,则点
,则点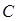 的轨迹方程是( )
的轨迹方程是( )
A. B.
B.
C.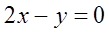 D.
D.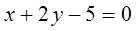
科目:gzsx 来源:2011-2012学年河北省高三上学期2月份月考文科数学试卷 题型:选择题
在平面直角坐标系中,O为原点,已知两点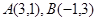 ,若
,若 满足
满足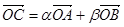 其中
其中 且
且 ,则点
,则点 的轨迹方程是( )
的轨迹方程是( )
A.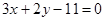 B.
B.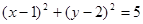 C.
C. D.
D.
科目:gzsx 来源:2011-2012学年河北省五校联盟高三模拟考试文科数学试卷 题型:选择题
在平面直角坐标系中,O为原点,已知两点 ,若
,若 满足
满足 其中
其中 且
且 ,则点
,则点 的轨迹方程是( )
的轨迹方程是( )
A. B.
B. C.
C. D.
D.
科目:czsx 来源: 题型:单选题



科目:czsx 来源:2011年浙江省湖州市部分学校中考数学三模试卷(解析版) 题型:选择题

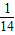
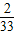
科目:czsx 来源:2016年初中毕业升学考试(浙江金华卷)数学(解析版) 题型:解答题
在平面直角坐标系中,点O为原点,平行于x轴的直线与抛物线L:y=ax2相交于A,B两点(点B在第一象限),点D在AB的延长线上.
(1)已知a=1,点B的纵坐标为2.
①如图1,向右平移抛物线L使该抛物线过点B,与AB的延长线交于点C,求AC的长.
②如图2,若BD=AB,过点B,D的抛物线L2,其顶点M在x轴上,求该抛物线的函数表达式.
(2)如图3,若BD=AB,过O,B,D三点的抛物线L3,顶点为P,对应函数的二次项系数为a3,过点P作 PE∥x轴,交抛物线L于E,F两点, 求
PE∥x轴,交抛物线L于E,F两点, 求 的值,并直接写出
的值,并直接写出 的值.
的值.

科目:czsx 来源: 题型:解答题

科目:czsx 来源: 题型:
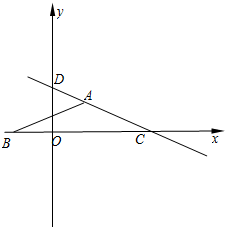 在x轴上,BC=8,AB=AC,直线AC与y轴相交于点D.
在x轴上,BC=8,AB=AC,直线AC与y轴相交于点D.科目:czsx 来源: 题型:
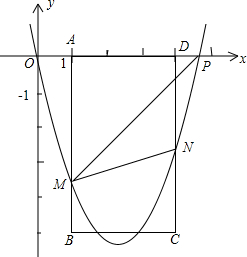 的速度运动t秒(t>0),抛物线y=x2+bx+c经过点O和点P,已知矩形ABCD的三个顶点为 A (1,0),B (1,-5),D (4,0).
的速度运动t秒(t>0),抛物线y=x2+bx+c经过点O和点P,已知矩形ABCD的三个顶点为 A (1,0),B (1,-5),D (4,0).| 21 | 8 |
科目:czsx 来源:2013年四川省自贡市高级中等学校招生考试数学 题型:013
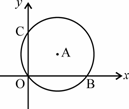
如图,在平面直角坐标系中,⊙A经过原点O,并且分别与x轴、y轴交于B、C两点,已知B(8,0),C(0,6),则⊙A的半径为
A.3
B.4
C.5
D.8
科目:czsx 来源:2011河北省中考数学试题 题型:044
如图,在平面直角坐标系中,点P从原点O出发,沿x轴向右以毎秒1个单位长的速度运动t秒(t>0),抛物线y=x2+bx+c经过点O和点P,已知矩形ABCD的三个顶点为A(1,0),B(1,-5),D(4,0).
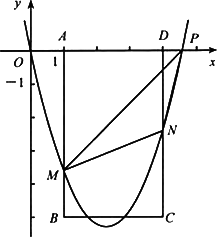
(1)求c,b(用含t的代数式表示):
(2)当4<t<5时,设抛物线分别与线段AB,CD交于点M,N.
①在点P的运动过程中,你认为∠AMP的大小是否会变化?若变化,说明理由;若不变,求出∠AMP的值;
②求△MPN的面积S与t的函数关系式,并求t为何值时,S=![]() ;
;
(3)在矩形ABCD的内部(不含边界),把横、纵坐标都是整数的点称为“好点”.若抛物线将这些“好点”分成数量相等的两部分,请直接写出t的取值范围.
科目:czsx 来源:江苏省苏州工业园区星海中学2012届九年级中考二模数学试题 题型:044
如图,在平面直角坐标系中,点P从原点O出发,沿x轴向右以毎秒1个单位长的速度运动t秒(t>0),抛物线y=x2+bx+c经过点O和点P,已知矩形ABCD的三个顶点为A(1,0),B(1,-5),D(4,0).
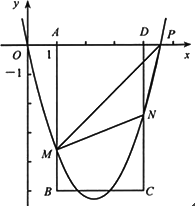
(1)求c,b(用含t的代数式表示):
(2)当4<t<5时,设抛物线分别与线段AB,CD交于点M,N.
①在点P的运动过程中,你认为cos∠AMP的大小是否会变化?若变化,说明理由;若不变,求出cos∠AMP的值;
②求△MPN的面积S与t的函数关系式,并求t为何值时,![]() ;
;
(3)在矩形ABCD的内部(不含边界),把横、纵坐标都是整数的点称为“好点”.若抛物线将这些“好点”分成数量相等的两部分,请直接写出t的取值范围是________.
科目:czsx 来源: 题型:解答题
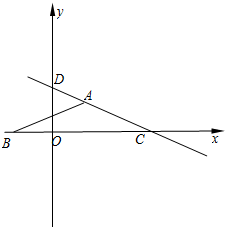 在x轴上,BC=8,AB=AC,直线AC与y轴相交于点D.
在x轴上,BC=8,AB=AC,直线AC与y轴相交于点D.科目:czsx 来源: 题型:解答题
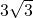 ),将△OAC绕AC的中点旋转180°,点O
),将△OAC绕AC的中点旋转180°,点O 落到点B的位置,抛物线
落到点B的位置,抛物线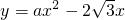 经过点A,点D是抛物线的顶点.
经过点A,点D是抛物线的顶点.科目:czsx 来源: 题型:解答题
 如图,在平面直角坐标系中,点O为原点,已知点A的坐标为(2,2),点B、C在y轴上,BC=8,AB=AC,直线AB与x轴相交于点D.
如图,在平面直角坐标系中,点O为原点,已知点A的坐标为(2,2),点B、C在y轴上,BC=8,AB=AC,直线AB与x轴相交于点D.科目:czsx 来源: 题型:解答题
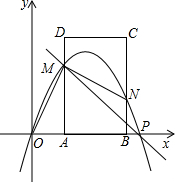 (t>0),抛物线y=-x2+bx经过点O和点P.已知矩形ABCD的三个顶点为A(1,0),B(3,0),D(1,3).
(t>0),抛物线y=-x2+bx经过点O和点P.已知矩形ABCD的三个顶点为A(1,0),B(3,0),D(1,3).