科目:czsx 来源: 题型:
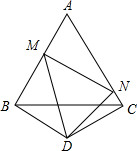 已知△ABC是边长为1cm的等边三角形,以BC为边作等腰三角形BCD,使得DB=DC,且∠BDC=120°,点M是AB边上的一个动点,作∠MDN交AC边于点N,且满足∠MDN=60°,则△AMN的周长为
已知△ABC是边长为1cm的等边三角形,以BC为边作等腰三角形BCD,使得DB=DC,且∠BDC=120°,点M是AB边上的一个动点,作∠MDN交AC边于点N,且满足∠MDN=60°,则△AMN的周长为科目:czsx 来源: 题型:填空题
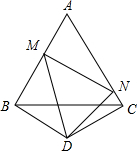 已知△ABC是边长为1cm的等边三角形,以BC为边作等腰三角形BCD,使得DB=DC,且∠BDC=120°,点M是AB边上的一个动点,作∠MDN交AC边于点N,且满足∠MDN=60°,则△AMN的周长为________.
已知△ABC是边长为1cm的等边三角形,以BC为边作等腰三角形BCD,使得DB=DC,且∠BDC=120°,点M是AB边上的一个动点,作∠MDN交AC边于点N,且满足∠MDN=60°,则△AMN的周长为________.科目:czsx 来源:2013年4月中考数学模拟试卷(57)(解析版) 题型:填空题

科目:czsx 来源:2013年5月中考数学模拟试卷(14)(解析版) 题型:填空题

科目:czsx 来源:2013年5月中考数学模拟试卷(11)(解析版) 题型:填空题

科目:czsx 来源:2013年4月中考数学模拟试卷(12)(解析版) 题型:填空题

科目:czsx 来源:2012年广东省深圳市中考数学模拟试卷(九)(解析版) 题型:填空题

科目:czsx 来源:广东省期末题 题型:解答题

 ,求BF的长;
,求BF的长;科目:czsx 来源:期末题 题型:解答题
 ,求BF的长;
,求BF的长;
科目:czsx 来源: 题型:
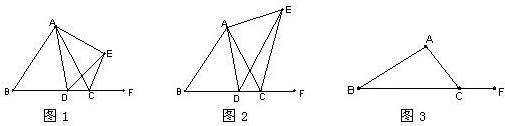
 如图,已知△ABC是等边三角形,D为AC上一个动点,延长AB至E,使BE=CD,连接DE交BC于点F.
如图,已知△ABC是等边三角形,D为AC上一个动点,延长AB至E,使BE=CD,连接DE交BC于点F.科目:czsx 来源: 题型:
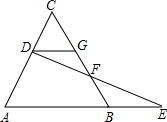 如图,已知△ABC是等边三角形,D为AC边上的一个动点,DG∥AB,延长AB到E,使BE=CD,连结DE交BC于F.
如图,已知△ABC是等边三角形,D为AC边上的一个动点,DG∥AB,延长AB到E,使BE=CD,连结DE交BC于F.科目:czsx 来源: 题型:解答题
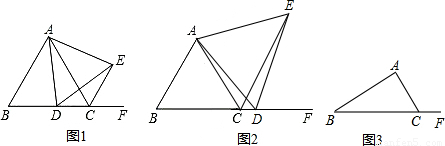
 如图,在△ABC中,∠C=90°,BC、AC、AB边的长分别记为a、b、c,点E是BC边上一个动点(点E与点B、C不重合),连接AE.已知a、b满足$\left\{\begin{array}{l}{b-6=0}\\{2a-b=10}\end{array}\right.$,且c是不等式组$\left\{\begin{array}{l}{\frac{x+12}{4}≤x+6}\\{\frac{2x+2}{3}>x-3}\end{array}\right.$的最大整数解.
如图,在△ABC中,∠C=90°,BC、AC、AB边的长分别记为a、b、c,点E是BC边上一个动点(点E与点B、C不重合),连接AE.已知a、b满足$\left\{\begin{array}{l}{b-6=0}\\{2a-b=10}\end{array}\right.$,且c是不等式组$\left\{\begin{array}{l}{\frac{x+12}{4}≤x+6}\\{\frac{2x+2}{3}>x-3}\end{array}\right.$的最大整数解.科目:czsx 来源: 题型:
科目:czsx 来源: 题型:解答题

科目:czsx 来源:2009-2010学年北京市清华附中九年级(上)统练数学试卷(7)(解析版) 题型:解答题
科目:czsx 来源:2008-2009学年北京市海淀区九年级(上)期中数学试卷(解析版) 题型:解答题

科目:czsx 来源:2012年湖北省武汉市中考数学模拟试卷(三)(解析版) 题型:解答题

科目:czsx 来源:2012年湖北省武汉市武昌区洪山区部分学校联考初三数学试卷(解析版) 题型:解答题
科目:czsx 来源: 题型:
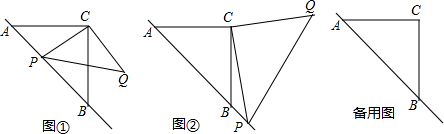
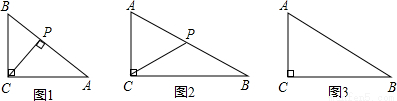
已知:△ABC是等腰三角形,动点P在斜边AB所在的直线上,以PC为直角边作等腰三角形PCQ,其中∠PCQ=90°,探究并解决下列问题:
(1)如图①,若点P在线段AB上,且AC=1+ ,PA=
,PA= ,则:
,则:
①线段PB=  ,PC= 2 ;
,PC= 2 ;
②猜想:PA2,PB2,PQ2三者之间的数量关系为 PA2+PB2=PQ2 ;
(2)如图②,若点P在AB的延长线上,在(1)中所猜想的结论仍然成立,请你利用图②给出证明过程;
(3)若动点P满足 =
= ,求
,求 的值.(提示:请利用备用图进行探求)
的值.(提示:请利用备用图进行探求)

科目:czsx 来源: 题型:解答题