科目:czsx 来源: 题型:
在平面直角坐标系中,O为原点,四边形OABC的顶点A在 轴的正半轴上,OA=4,OC=2,点P,点Q分别是边BC,边AB上的点,连结AC,PQ,点B1是点B关于PQ的对称点。【版权所有:21教育】
轴的正半轴上,OA=4,OC=2,点P,点Q分别是边BC,边AB上的点,连结AC,PQ,点B1是点B关于PQ的对称点。【版权所有:21教育】
(1)若四边形PABC为矩形,如图1,
①求点B的坐标;
②若BQ:BP=1:2,且点B1落在OA上,求点B1的坐标;
(2)若四边形OABC为平行四边形,如图2,且OC⊥AC,过点B1作B1F∥ 轴,与对角线AC、边OC分别交于点E、点F。若B1E: B1F=1:3,点B1的横坐标为
轴,与对角线AC、边OC分别交于点E、点F。若B1E: B1F=1:3,点B1的横坐标为 ,求点B1的纵坐标,并直接写出
,求点B1的纵坐标,并直接写出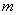 的取值范围。2-1-c-n-j-y
的取值范围。2-1-c-n-j-y

科目:czsx 来源: 题型:
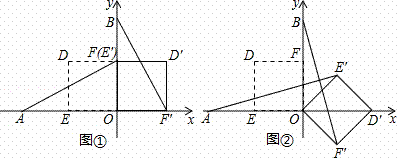
在平面直角坐标系中,O为原点,点A(﹣2,0),点B(0,2),点E,点F分别为OA,OB的中点.若正方形OEDF绕点O顺时针旋转,得正方形OE′D′F′,记旋转角为α.
(1)如图①,当α=90°时,求AE′,BF′的长;
(2)如图②,当α=135°时,求证AE′=BF′,且AE′⊥BF′;21世纪教育网
(3)直线AE′与直线BF′相交于点P,当点P在坐标轴上时,分别表示出此时点E′、D′、F′的坐标(直接写出结果即可).www-2-1-cnjy-com
科目:czsx 来源: 题型:阅读理解
 九年义务教育三年制初级中学教科书代数第三册中,有以下几段文字:“对于坐标平面内任意一点M,都有唯一的一对有序实数(x,y)和它对应;对于任意一对有序实数(x,y),在坐标平面内都有唯一的一点M和它对应,也就是说,坐标平面内的点与有序实数对是一一对应的.”“一般地,对于一个函数,如果把自变量x与函数y的每对对应值分别作为点的横坐标与纵坐标,在坐标平面内描出相应的点,这些点所组成的图形,就是这个函数的图象.”“实际上,所有一次函数的图象都是一条直线.”“因为两点确定一条直线,所以画一次函数的图象时,只要先描出两点,再连成直线,就可以了.”由此可知:满足函数关系式的有序实数对所对应的点,一定在这个函数的图象上;反之,函数图象上的点的坐标,一定满足这个函数的关系式.另外,已知直线上两点的坐标,便可求出这条直线所对应的一次函数的解析式.
九年义务教育三年制初级中学教科书代数第三册中,有以下几段文字:“对于坐标平面内任意一点M,都有唯一的一对有序实数(x,y)和它对应;对于任意一对有序实数(x,y),在坐标平面内都有唯一的一点M和它对应,也就是说,坐标平面内的点与有序实数对是一一对应的.”“一般地,对于一个函数,如果把自变量x与函数y的每对对应值分别作为点的横坐标与纵坐标,在坐标平面内描出相应的点,这些点所组成的图形,就是这个函数的图象.”“实际上,所有一次函数的图象都是一条直线.”“因为两点确定一条直线,所以画一次函数的图象时,只要先描出两点,再连成直线,就可以了.”由此可知:满足函数关系式的有序实数对所对应的点,一定在这个函数的图象上;反之,函数图象上的点的坐标,一定满足这个函数的关系式.另外,已知直线上两点的坐标,便可求出这条直线所对应的一次函数的解析式.科目:czsx 来源:1999年河北省中考数学试卷 题型:解答题
科目:czsx 来源: 题型:
下列是由四个相同小正方体摆成的立方体图形,它的俯视图是( )
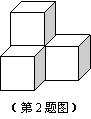
| A. B. C. D. |
1. 我州今年参加中考的学生人数大约为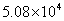 人,对于这个科学记数法表示的近似数,下列说法正确的是( )
人,对于这个科学记数法表示的近似数,下列说法正确的是( )
A.精确到百分位,有3个有效数字 B.精确到百分位,有5个有效数字
C.精确到百位,有3个有效数字 D.精确到百位,有5个有效数字
2. 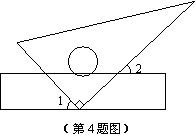 如图,将一块三角板的执教顶点放在直尺的一边上,当
如图,将一块三角板的执教顶点放在直尺的一边上,当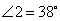 时,
时,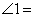 ( )
( )
A. B.
B. C.
C. D.
D.
3. 下列根式中,不能与 合并的是( )
合并的是( )
A.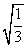 B.
B.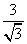 C.
C.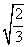 D.
D.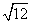
某班45名同学某天每人的生活费用统计如下表:
| 生活费(元) | 10 | 15 | 20 | 25 | 30 |
| 学生人数(人) | 4 | 10 | 15 | 10 | 6 |
对于这45名同学这天每人的生活费用,下列说法不正确的是( )A.平均数是20 B.众数 C.中位数是20 D.极差是2021世纪教育网版权所有
4. 关于 的一元二次方程
的一元二次方程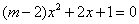 有实数根,则
有实数根,则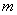 的取值范围是( )
的取值范围是( )
A.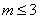 B.
B. C.
C. 且
且 D.
D.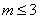 且
且
5. 将圆心角为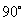 ,面积为
,面积为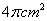 的扇形围成一个圆锥的侧面,则所围成圆锥的底面半径为( )
的扇形围成一个圆锥的侧面,则所围成圆锥的底面半径为( )
A.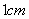 B.
B.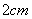 C.
C.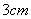 D.
D.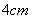
6. 在平面直角坐标系中,点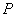 (
(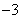 ,2)关于直线
,2)关于直线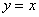 对称点的坐标是( )
对称点的坐标是( )
A.(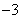 ,
,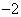 ) B.(3,2) C.(2,
) B.(3,2) C.(2,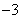 ) D.(3,
) D.(3,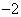 )
)
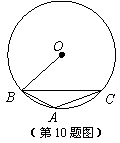
7. 如图,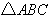 内接于
内接于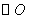 ,
,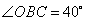 ,则
,则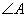 的度数为( )
的度数为( )
A.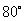 B.
B.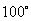 C.
C.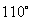 D.
D.
8. 以正方形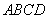 两条对角线的交点
两条对角线的交点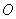 为坐标原点,建立如图所示的平面直角坐标系,双曲线
为坐标原点,建立如图所示的平面直角坐标系,双曲线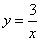 经过点
经过点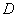 ,则正方形
,则正方形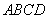 的面积是( )21·cn·jy·com
的面积是( )21·cn·jy·com
A.10 B.11 C.12 D.13
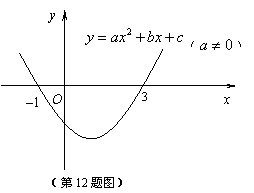
9. 二次函数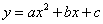 (
(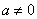 )的图象如图所示,下列说法:①
)的图象如图所示,下列说法:①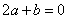 ;②当
;②当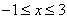 时,
时,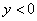 ;③若点(
;③若点(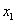 ,
,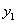 )和点(
)和点(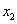 ,
,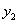 )都在函数的图象上,当
)都在函数的图象上,当 时,
时,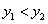 ;④
;④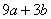
 。其中正确的是( )21·世纪*教育网
。其中正确的是( )21·世纪*教育网
A.① ② ④ B.① ④ C.① ② ③ D.③ ④

第II卷(选择题 共72分)
二、填空题:(共5个小题,每小题4分,共20分)
10. 的平方根是 。
的平方根是 。
11.已知函数 是正比例函数,则
是正比例函数,则 ,
,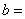 。
。
12.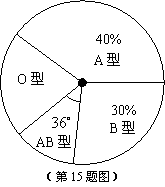 小明同学根据全班同学的血型绘制了如图所示的扇形统计图,已知
小明同学根据全班同学的血型绘制了如图所示的扇形统计图,已知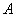 型血的有20人,则
型血的有20人,则 型血的有 人。21教育网
型血的有 人。21教育网
13.分式方程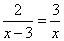 的解是 。
的解是 。
14.在
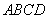 中,
中, 、
、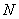 是
是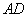 边上的三等分点,连接
边上的三等分点,连接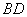 、
、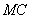 相交于
相交于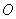 点,则
点,则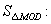
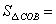 。2-1-c-n-j-y
。2-1-c-n-j-y
三、解答题:(共2小题,每小题6分,共12分)
15.计算: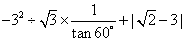 ;
;
16.先化简: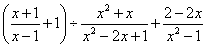 ,然后从
,然后从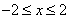 的范围内选取一个合适的整数作为
的范围内选取一个合适的整数作为 的值代入求值。
的值代入求值。
四、解答题:(共3小题,每小题8分,共24分)
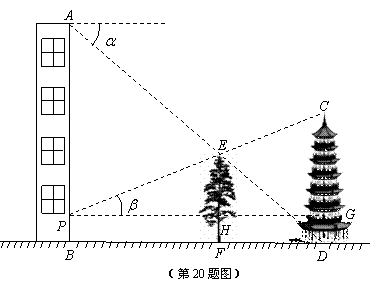
17.如图,在楼房 和塔
和塔 之间有一棵树
之间有一棵树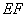 ,从楼顶
,从楼顶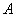 处经过树顶
处经过树顶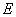 点恰好看到塔的底部
点恰好看到塔的底部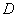 点,且俯角
点,且俯角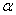 为
为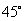 ,从楼底
,从楼底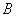 点1米的
点1米的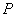 点处经过树顶
点处经过树顶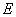 点恰好看到塔的顶部
点恰好看到塔的顶部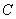 点,且仰角
点,且仰角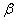 为
为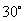 。已知树高
。已知树高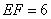 米,求塔
米,求塔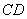 的高度(结果保留根号)。
的高度(结果保留根号)。
18.如图,在正方形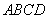 中,
中,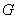 是
是 上任意一点,连接
上任意一点,连接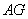 ,
,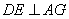 于
于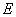 ,
,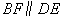 交
交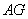 于
于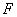 ,探究线段
,探究线段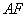 、
、 、
、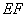 三者之间的数量关系,并说明理由。
三者之间的数量关系,并说明理由。
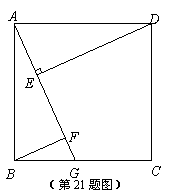
19.2015年5月6日,凉山州政府在邛海“空列”项目考察座谈会上与多方达成初步合作意向,决定共同出资60.8亿元,建设40千米的环邛海空中列车,这将是国内第一条空中列车。据计算,将有24千米的“空列”轨道假设在水上,其余假设在陆地上,并且每千米水上建设费用比陆地建设费用多0.2亿元。 21*cnjy*com
(1)求每千米 “空列”轨道的水上建设费用和陆地建设费用各需多少亿元?
(2)设计在某段“空列”轨道的建设中,每天至少需要运送沙石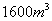 ,施工方准备租用大、小两种运输车共十辆。已知每辆大车每天运送沙石
,施工方准备租用大、小两种运输车共十辆。已知每辆大车每天运送沙石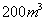 ,每辆小车每天运送沙石
,每辆小车每天运送沙石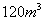 ,大、小车每天每辆租车费用分别是1000元,700元,且要求每天租车的总费用不得超过9300元,问施工方有几种租车方案?那种租车方案费用最低,最低费用是多少?
,大、小车每天每辆租车费用分别是1000元,700元,且要求每天租车的总费用不得超过9300元,问施工方有几种租车方案?那种租车方案费用最低,最低费用是多少?
五、解答题:(共2小题,每小题8分,共16分)
20.有甲、乙两个不透明的布袋,甲袋中装有3个完全相同的小球,分别标有数字0、1、2;乙袋中装有3个完全相同的小球,分别标有数字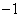 、
、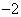 、0;先从甲袋中随机取出一个小球,记录标有的数字为
、0;先从甲袋中随机取出一个小球,记录标有的数字为 ,再从乙袋中随机取出一个小球,记录标有的数字为
,再从乙袋中随机取出一个小球,记录标有的数字为 ,确定点
,确定点 (
( ,
, )。www.21-cn-jy.com
)。www.21-cn-jy.com
(1)用树状图或列表法列举点 所有可能的坐标;
所有可能的坐标;
(2)求点 (
( ,
, )在函数
)在函数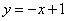 的图象上的概率 ;
的图象上的概率 ;
(3)在平面直角坐标系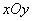 中,
中,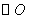 的半径是2,求过点
的半径是2,求过点 (
( ,
, )能作
)能作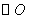 的切线的概率;
的切线的概率;
21.阅读理解:
材料1:一组对边平行,另一组对边不平行的四边形叫梯形。其中平行的两边叫做梯形的底边,不平行的两边叫做梯形的腰。连接梯形两腰中点的线段叫做梯形的中位线。
 梯形的中位线具有下列性质:
梯形的中位线具有下列性质:
梯形的中位线平行于两底,并且等于两底和的一半。
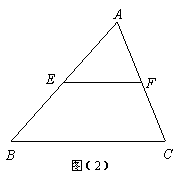
如图(1),在梯形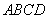 中,
中,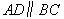 。
。
∵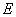 、
、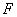 分别是
分别是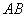 、
、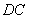 的中点,
的中点,
∴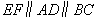 ,
,
 。
。
材料2:经过三角形一边的中点与另一边平行的直线必平分第三边。
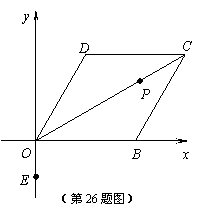
如图(2),在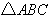 中,∵
中,∵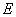 是
是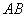 的中点,
的中点, ,
,
∴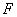 是
是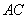 的中点。
的中点。
请你运用所学知识,结合上述材料,解答下列问题:
如图(3),在梯形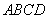 中,
中,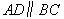 ,
,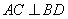 于
于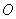 ,
, 、
、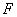 分别是
分别是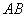 、
、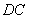 的中点,
的中点,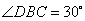 。
。
(1)求证: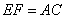 ;
;
(2)若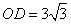 ,
,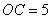 ,求
,求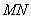 的长。
的长。

B卷(共30分)
 二、填空题:(共2小题,每小题5分,共10分)
二、填空题:(共2小题,每小题5分,共10分)
22.已知实数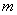 、
、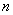 满足
满足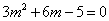 ,
,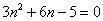 ,则
,则 。
。
23.菱形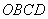 在平面直角坐标系中的位置如图所示,顶点
在平面直角坐标系中的位置如图所示,顶点 (2,0),
(2,0),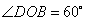 ,点
,点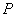 是对角线
是对角线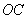 上一个动点,
上一个动点, 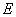 (0,
(0,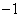 ),当
),当 最短时,点
最短时,点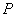 的坐标为 。2·1·c·n·j·y
的坐标为 。2·1·c·n·j·y
二、解答题:(共2小题,27题8分,28题12分,共20分)
24.如图,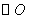 的半径为5,点
的半径为5,点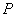 在
在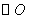 外,
外,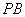 交
交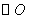 于
于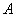 、
、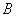 两点,
两点,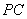 交
交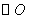 于
于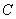 、
、 两点。
两点。
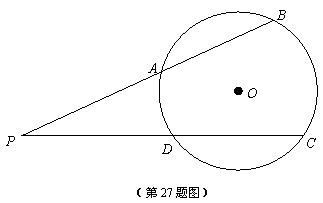 (1)求证:
(1)求证: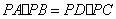 ;(2)若
;(2)若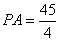 ,
,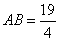 ,
,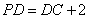 ,求点
,求点 到
到 的距离。
的距离。
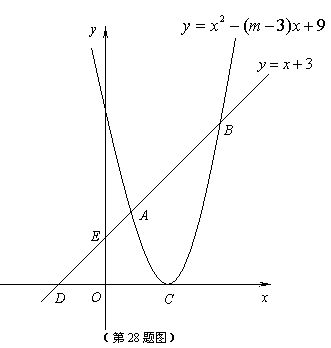
25.如图,已知抛物线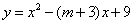 的顶点
的顶点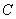 在
在 轴的正半轴上,一次函数
轴的正半轴上,一次函数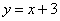 与抛物线交于
与抛物线交于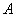 、
、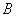 两点,与
两点,与 、
、 轴分别交于
轴分别交于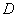 、
、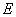 两点。
两点。
(1)求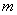 的值;
的值;
(2)求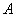 、
、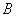 两点的坐标;
两点的坐标;
(3)点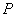 (
(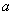 ,
,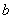 )(
)(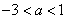 )是抛物线上一点,当
)是抛物线上一点,当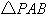 得面积是
得面积是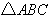 面积的2倍时,求
面积的2倍时,求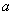 、
、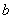 的值。
的值。