
在平面直角坐标系中,O为原点,点A(﹣2,0),点B(0,2),点E,点F分别为OA,OB的中点.若正方形OEDF绕点O顺时针旋转,得正方形OE′D′F′,记旋转角为α.
(1)如图①,当α=90°时,求AE′,BF′的长;
(2)如图②,当α=135°时,求证AE′=BF′,且AE′⊥BF′;21世纪教育网
(3)直线AE′与直线BF′相交于点P,当点P在坐标轴上时,分别表示出此时点E′、D′、F′的坐标(直接写出结果即可).www-2-1-cnjy-com
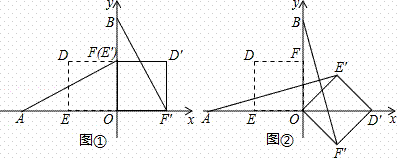
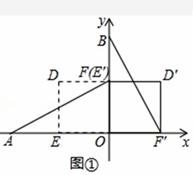
解:(1)当α=90°时,点E′与点F重合,如图①.
∵点A(﹣2,0)点B(0,2),
∴OA=OB=2.
∵点E,点F分别为OA,OB的中点,
∴OE=OF=1
∵正方形OE′D′F′是正方形OEDF绕点O顺时针旋转90°得到的,
 ∴OE′=OE=1,OF′=OF=1.
∴OE′=OE=1,OF′=OF=1.
在Rt△AE′O中,
AE′=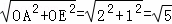 .
.
在Rt△BOF′中,
BF′=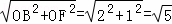 .
.
∴AE′,BF′的长都等于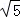 . ———————————————4分
. ———————————————4分
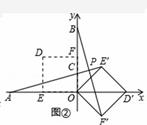
(2)当α=135°时,如图②.
∵正方形OE′D′F′是由正方形OEDF绕点O顺时针旋转135°所得,
∴∠AOE′=∠BOF′=135°.
在△AOE′和△BOF′中,
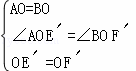 ,
,
∴△AOE′≌△BOF′(SAS).
∴AE′=BF′,且∠OAE′=∠OBF′.
∵∠ACB=∠CAO+∠AOC=∠CBP+∠CPB,∠CAO=∠CBP,
∴∠CPB=∠AOC=90°
∴AE′⊥BF′.——————————————————————9分
(3)点E′(2,0)、D′(2,-2)、F′(0,-2)……12分


 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:
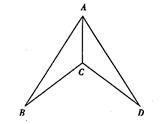
如图,在△ABC和△ACD中,CB=CD,设点E是CB的中点,
点F是CD的中点.
(1) 请你在图中作出点E和点F(要求用尺规作图,保留作图痕迹,不写作法与证明);
(2) 连接AE、AF,若∠ACB=∠ACD,则△ACE与△ACF全等吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
现有A、B两枚均匀的小立方体(立方体的每个面上分别标有数字1,2,3,4,5,6).用小莉掷A立方体朝上的数字为x、小明掷B立方体朝上的数字为y来确定点P(x,y),那么它们各掷一次所确定的点P落在已知抛物线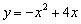 上的概率为( )
上的概率为( )
A.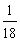 B.
B.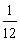 C.
C. D.
D.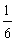
查看答案和解析>>
科目:初中数学 来源: 题型:
2015年3月份,苏州市某周的日最高气温统计如下表:则这七天中日最高气温的众数和中位数分别是 ( )

A.4,4 B.5,4 C.4,3 D.4,4.5
查看答案和解析>>
科目:初中数学 来源: 题型:
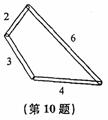
如图,用四个螺丝将四条不可弯曲的木条围成一个木框,不计
螺丝大小,其中相邻两螺丝的距离依次为2、3、4、6,且相邻两木
条的夹角均可调整.若调整木条的夹角时不破坏此木框,则任意两
个螺丝间的距离的最大值为 ( )
A.6 B.7
C.8 D.10
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
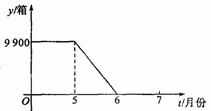
某消毒液工厂,去年5月份以前,每天的产量与销售量均为500箱,进入5月份后,每天的产量保持不变,市场需求量不断增加,如图是5月前后一段时期库存量y(箱)与生产时间t(月份)之间的函数图像.(5月份以30天计算)
(1)该厂_______月份开始出现供不应求的现象,5月份的平均日销售量为_______箱;
(2)为满足市场需求,该厂打算在投资不超过220万元的情况下,购买8台新设备,使扩大生产规模后的日产量不低于5月份的平均日销售量,现有A、B两种型号的设备可供选择,其价格与两种设备的日产量如下表:

请设计一种购买设备的方案,使得日产量最大;
(3)在(2)的条件下(市场日平均需求量与5月份相同),若安装设备需5天(6月6日新设备开始生产),指出何时开始该厂有库存.
查看答案和解析>>
科目:初中数学 来源: 题型:
下列条件中,可以确定△ABC和△A′B′C′全等的是( )
A. BC=BA ,B′C′=B′A′,∠B=∠B′B. ∠A=∠B′,AC=A′B′,AB=B′C′
C. ∠A=∠A′,AB=B′C′,AC=A′C′ D. BC=B′C′,AC=A′B′,∠B=∠C′
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com