科目:gzsx 来源: 题型:
科目:gzwl 来源: 题型:实验题
科目:gzwl 来源: 题型:实验题

科目:gzwl 来源: 题型:解答题

科目:czsx 来源: 题型:
科目:czsx 来源: 题型:解答题
科目:czsx 来源:2013年江苏省无锡市天一实验学校中考数学三模试卷(解析版) 题型:解答题
科目:czsx 来源:2013年江苏省南京市中考数学模拟试卷(二)(解析版) 题型:解答题
科目:czsx 来源:2012年5月中考数学模拟试卷(50)(解析版) 题型:解答题
科目:czsx 来源:2011年江苏省南京市白下区中考数学一模试卷(解析版) 题型:解答题
科目:czsx 来源: 题型:
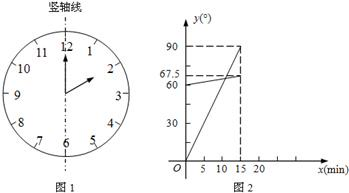
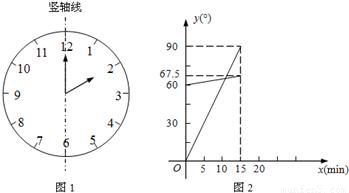
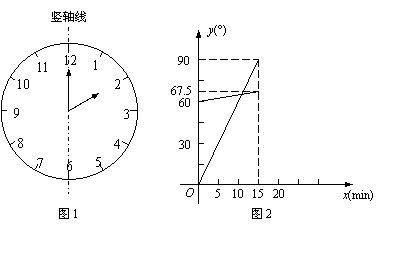
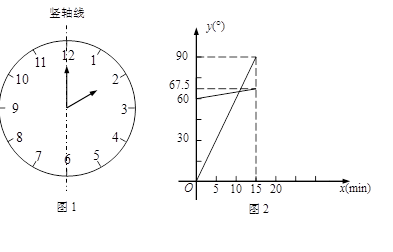
(1)在遇到问题:“钟面上,如果把时针与分针看作是同一平面内的两条线段,在2∶00~2∶15之间,时针与分针重合的时刻是多少?”时,小明尝试运用建立函数关系的方法:
①恰当选取变量x和y.小明设2点钟之后经过x min(0≤x≤15),时针、分针分别与竖轴线(即经过表示“12”和“6”的点的直线,如图1)所成的角的度数为y1°、y2°;
②确定函数关系.由于时针、分针在单位时间内转动的角度不变,因此既可以直接写出y1、y2关于x的函数关系式,也可以画出它们的图象.小明选择了后者,画出了图2;
③根据题目的要求,利用函数求解.本题中小明认为求出两个图象交点的横坐标就可以解决问题.
请你按照小明的思路解决这个问题.
 |
(2)请运用建立函数关系的方法解决问题:钟面上,如果把时针与分针看作是同一平面内的两条线段,在7∶30~8∶00之间,时针与分针互相垂直的时刻是多少?
科目:czsx 来源: 题型:阅读理解
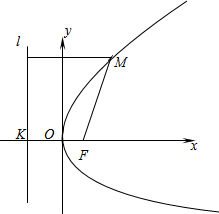 先阅读短文,再回答短文后面的问题.
先阅读短文,再回答短文后面的问题.| p |
| 2 |
| p |
| 2 |
(x-
|
| p |
| 2 |
(x-
|
| p |
| 2 |
| p |
| 2 |
| p |
| 2 |
| 标准方程 | 交点坐标 | 准线方程 | ||||
| y2=2px(p>0) | (
|
x=-
| ||||
| y2=-2px(p>0) | (-
|
x=
| ||||
| x2=2py(p>0) | (0,
|
y=-
| ||||
| x2=-2py(p>0) | (0,-
|
y=-
|
| 3 |
科目:czsx 来源: 题型:解答题
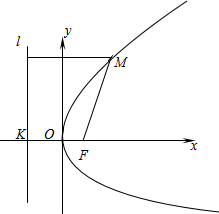 先阅读短文,再回答短文后面的问题.
先阅读短文,再回答短文后面的问题. ,0),准线l的方程为x=-
,0),准线l的方程为x=- .
.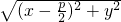 ,d=|x+
,d=|x+ |∴
|∴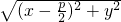 =|x+
=|x+ |
| ,0),它的准线方程是x=-
,0),它的准线方程是x=- .
.| 标准方程 | 交点坐标 | 准线方程 |
| y2=2px(p>0) | (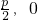 ) ) | x=- |
| y2=-2px(p>0) | (-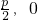 ) ) | x= |
| x2=2py(p>0) | (0, ) ) | y=- |
| x2=-2py(p>0) | (0,- ) ) | y=- |
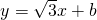 经过抛物线y2=4x的焦点,与抛物线相交于两点A、B,求线段AB的长.
经过抛物线y2=4x的焦点,与抛物线相交于两点A、B,求线段AB的长. 科目:czsx 来源: 题型:
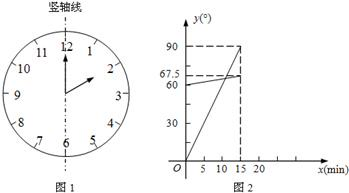
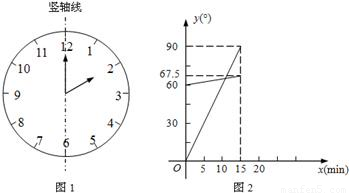
(8分)(1)在遇到问题:“钟面上,如果把时针与分针看作是同一平面内的两条线段,在2∶00~2∶15之间,时针与分针重合的时刻是多少?”时,小明尝试运用建立函数关系的方法:
①恰当选取变量x和y.小明设2点钟之后经过x min(0≤x≤15),时针、分针分别与竖轴线(即经过表示“12”和“6”的点的直线,如图1)所成的角的度数为y1°、y2°;
②确定函数关系.由于时针、分针在单位时间内转动的角度不变,因此既可以直接写出y1、y2关于x的函数关系式,也可以画出它们的图象.小明选择了后者,画出了图2;
③根据题目的要求,利用函数求解.本题中小明认为求出两个图象交点的横坐标就可以解决问题.
请你按照小明的思路解决这个问题.
(2)请运用建立函数关系的方法解决问题:钟面上,如果把时针与分针看作是同一平面内
的两条线段,在7∶30~8∶00之间,时针与分针互相垂直的时刻是多少?
科目:czsx 来源: 题型:

科目:czsx 来源:2010-2011学年南京市考数学一模试卷 题型:解答题
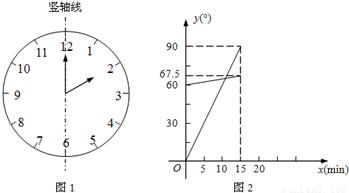
(8分)(1)在遇到问题:“钟面上,如果把时针与分针看作是同一平面内的两条线段,在2∶00~2∶15之间,时针与分针重合的时刻是多少?”时,小明尝试运用建立函数关系的方法:
①恰当选取变量x和y.小明设2点钟之后经过x min(0≤x≤15),时针、分针分别与竖轴线(即经过表示“12”和“6”的点的直线,如图1)所成的角的度数为y1°、y2°;
②确定函数关系.由于时针、分针在单位时间内转动的角度不变,因此既可以直接写出y1、y2关于x的函数关系式,也可以画出它们的图象.小明选择了后者,画出了图2;
③根据题目的要求,利用函数求解.本题中小明认为求出两个图象交点的横坐标就可以解决问题.
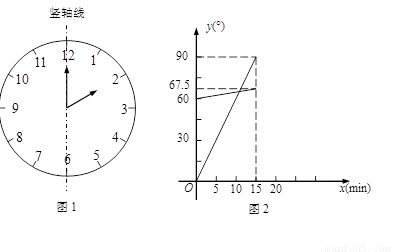
请你按照小明的思路解决这个问题.
(2)请运用建立函数关系的方法解决问题:钟面上,如果把时针与分针看作是同一平面内
的两条线段,在7∶30~8∶00之间,时针与分针互相垂直的时刻是多少?
科目:czsx 来源:不详 题型:解答题
 面上,如果把时针与分针看作是同一平面内的两条线段,在2∶00~2
面上,如果把时针与分针看作是同一平面内的两条线段,在2∶00~2 ∶15之间,时针与分针重合的时刻是多少?”时,小明尝试运用建立函数关系的方法:
∶15之间,时针与分针重合的时刻是多少?”时,小明尝试运用建立函数关系的方法:
 内
内科目:czsx 来源:2014-2015学年湖北省咸宁市中考模拟考试数学试卷(解析版) 题型:解答题
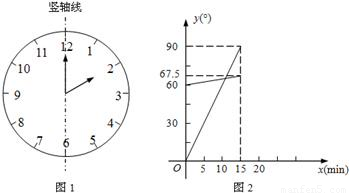
(本题满分10分)(1)在遇到问题:“钟面上,如果把时针与分针看作是同一平面内的两条线段,在2∶00~2∶15之间,时针与分针重合的时刻是多少?”时,小明尝试运用建立函数关系的方法:

①恰当选取变量x和y.小明设2点钟之后经过x min(0≤x≤15),时针、分针分别与竖轴线(即经过表示“12”和“6”的点的直线,如图1)所成的角的度数为y1°、y2°;
②确定函数关系.由于时针、分针在单位时间内转动的角度不变,因此既可以直接写出y1、y2关于x的函数关系式,也可以画出它们的图象.小明选择了后者,画出了图2;
③根据题目的要求,利用函数求解.本题中小明认为求出两个图象交点的横坐标就可以解决问题.
(2)请运用建立函数关系的方法解决问题:钟面上,如果把时针与分针看作是同一平面内的两条线段,在7∶30~8∶00之间,时针与分针互相垂直的时刻是多少?(请你按照小明的思路解决这个问题.)
科目:czsx 来源:江苏省无锡市天一实验学校2012届九年级一模数学试题 题型:044
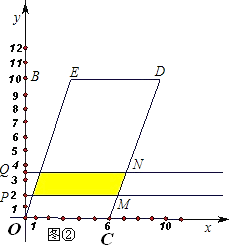
在平面直角坐标系中,点B的坐标为(0,10),点P、Q同时从O点出发,在线段OB上做往返运动,点P往返一次需10 s,点Q往返一次需6 s.设动点P、Q运动的时间为x( s),动点离开原点的距离是y.
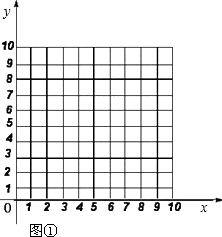
(1)当0≤x≤10时,在图①中,分别画出点P、点Q运动时关于x的函数图象,并回答:
①点P从O点出发,1个往返之间与点Q相遇几次(不包括O点)?
②点P从O点出发,几秒后与点Q第一次相遇?
(2)如图②,在平面直角坐标系中,□OCDE的顶点C(6,0),D、E、B在同一直线上.分别过点P、Q作PM、QN垂直于y轴,P、Q为垂足.设运动过程中两条直线PM,QN与□OCDE围成图形(阴影部分)的面积是S,试求当x(0≤x≤5)为多少秒时,S有最大值.最大值是多少?
科目:czsx 来源:2012年人教版八年级上第十一章全等三角形第二节全等三角形的判定练习卷(解析版) 题型:解答题
有一块不规则的鱼池,下面是两位同学分别设计的能够粗略地测量出鱼池两端A、B的距离的方案,请你分析一下两种方案的理由.
方案一:小明想出了这样一个方法,如图①所示,先在AB的垂线BF上取两点C、D,使CD=BC,再定出BF的垂线DE,使A、C、E在同一条直线上,测得DE的长就是AB的长. 你能说明一下这是为什么吗?
方案二:小军想出了这样一个方法,如图②所示,先在平地上取一个可以直接到达鱼池两端A、B的点C,连结AC并延长到点D,使CD=CA,连结BC并延长到E,使CE=CB,连结DE,量出DE的长,这个长就是A、B之间的距离. 你能说明一下这是为什么吗?