科目：czsx 来源： 题型：解答题

5．如图，在等腰△ABC中，AB=AC，点P为底边BC上一动点，连接AP，在AP左侧作等腰△APD，使PA=PD，∠APD=∠BAC，连接BD．
（1）如图①，若∠APD=∠BAC=60°，求证：△ABD≌△ACP；
（2）如图②，若∠APD=∠BAC=90°，AB=2，当点P由点C运动到点B时：
①∠PBD的大小是否为定值？若为定值，求出其大小，若发生变化，请说明理由；
②求出点D运动的路径长度

查看答案和解析>>

科目：czsx 来源： 题型：

在等腰△ABC中，已知AB=AC=5cm，BC=6cm，动点P、Q分别从A、B两点同时出发，沿AB、BC方向匀速移动，它们的速度都是1 cm/秒．当点P到达点B时，P、Q两点停止运动，设点P的运动时间为t（秒）．
（1）当t为何值时，PQ⊥AB？
（2）设四边形APQC的面积为ycm²，写出y关于t的函数关系式及定义域；
（3）分别以P、Q为圆心，PA、BQ长为半径画圆，若⊙P与⊙Q相切，求t的值；
（4）在P、Q运动中，△BPQ与△ABC能否相似？若能，请求出AP的长；若不能，请说明理由．

查看答案和解析>>

科目：czsx 来源： 题型：

在等腰△ABC中，已知AB=AC=3，cos∠B=

1

3

，D为AB上一点，过点D作DE⊥AB交BC边于点E，过点

E作EF⊥BC交AC边于点F．
（1）当BD长为何值时，以点F为圆心，线段FA为半径的圆与BC边相切；
（2）过点F作FP⊥AC，与线段DE交于点G，设BD长为x，△EFG的面积为y，求y关于x的函数解析式及其定义域．

查看答案和解析>>

科目：czsx 来源： 题型：

在等腰△ABC中，CD是底边AB上的高，E是腰BC的中点，AE与CD交于F，现给出三条路线：
（a）A→F→C→E→B→D→A；
（b）A→C→E→B→D→F→A；
（c）A→D→B→E→F→C→A；
它们的长度分别记为L（a）、L（b）及L（c），则L（a）＜L（b），L（a）＜L（c），L（b）＜L（c）中一定能成立的是

．

查看答案和解析>>

科目：czsx 来源：数学教研室 题型：044

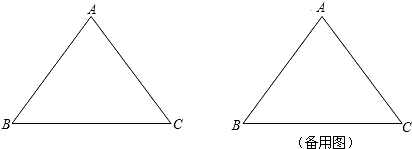
在等腰△ABC中，B、C为定点，且AC=AB，D为BC的中点，以BC为直径作⊙D．

(1)顶角A等于多少度时，点A在⊙D上？

(2)顶角A等于多少度时，点A在⊙D内部？

(3)顶角A等于多少度时，点A在⊙D外部？

查看答案和解析>>

科目：czsx 来源： 题型：044

在等腰△ABC中，B、C为定点，且AC=AB，D为BC的中点，以BC为直径作⊙D．

(1)顶角A等于多少度时，点A在⊙D上？

(2)顶角A等于多少度时，点A在⊙D内部？

(3)顶角A等于多少度时，点A在⊙D外部？

查看答案和解析>>

科目：czsx 来源： 题型：解答题

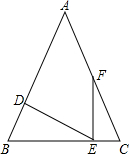
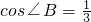在等腰△ABC中，已知AB=AC=3， $数学公式$ ，D为AB上一点，过点D作DE⊥AB交BC边于点E，过点E作EF⊥BC交AC边于点F．
（1）当BD长为何值时，以点F为圆心，线段FA为半径的圆与BC边相切；
（2）过点F作FP⊥AC，与线段DE交于点G，设BD长为x，△EFG的面积为y，求y关于x的函数解析式及其定义域．

查看答案和解析>>

科目：czsx 来源：2010年上海市静安区初三数学中考模拟试卷（12月份）（解析版） 题型：解答题

在等腰△ABC中，已知AB=AC=3，

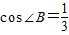，D为AB上一点，过点D作DE⊥AB交BC边于点E，过点E作EF⊥BC交AC边于点F．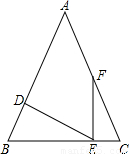
（1）当BD长为何值时，以点F为圆心，线段FA为半径的圆与BC边相切；
（2）过点F作FP⊥AC，与线段DE交于点G，设BD长为x，△EFG的面积为y，求y关于x的函数解析式及其定义域．

查看答案和解析>>

科目：czsx 来源： 题型：填空题

在等腰△ABC中，CD是底边AB上的高，E是腰BC的中点，AE与CD交于F，现给出三条路线：
（a）A→F→C→E→B→D→A；
（b）A→C→E→B→D→F→A；
（c）A→D→B→E→F→C→A；
它们的长度分别记为L（a）、L（b）及L（c），则L（a）＜L（b），L（a）＜L（c），L（b）＜L（c）中一定能成立的是________．

查看答案和解析>>

科目：czsx 来源： 题型：解答题

在等腰△ABC中，已知AB=AC=5cm，BC=6cm，动点P、Q分别从A、B两点同时出发，沿AB、BC方向匀速移动，它们的速度都是1 cm/秒．当点P到达点B时，P、Q两点停止运动，设点P的运动时间为t（秒）．
（1）当t为何值时，PQ⊥AB？
（2）设四边形APQC的面积为ycm²，写出y关于t的函数关系式及定义域；
（3）分别以P、Q为圆心，PA、BQ长为半径画圆，若⊙P与⊙Q相切，求t的值；
（4）在P、Q运动中，△BPQ与△ABC能否相似？若能，请求出AP的长；若不能，请说明理由．

查看答案和解析>>

科目：czsx 来源： 题型：解答题

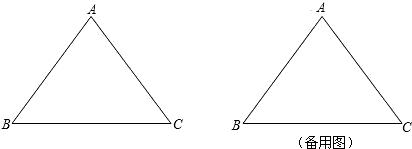
在等腰△ABC中，B、C为定点，且AC=AB，D为BC的中点，以BC为直径作⊙D，问：
（1）顶角A等于多少度时，点A在⊙D上？（2）顶角A等于多少度时，点A在⊙D内部？（3）顶角A等于多少度时，点A在⊙D外部？

查看答案和解析>>

科目：czsx 来源：上海模拟题 题型：解答题

在等腰△ABC中，已知AB=AC=3，cos∠B=

，D为AB上一点，过点D作DE⊥AB交BC边于点E，过点E作EF⊥BC交AC边于点F。
（1）当BD长为何值时，以点F为圆心，线段FA为半径的圆与BC边相切？
（2）过点F作FP⊥AC，与线段DE交于点G，设BD长为x，△EFG的面积为y，求y关于x的函数解析式及其定义域。

查看答案和解析>>

科目：czsx 来源： 题型：

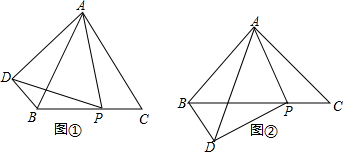
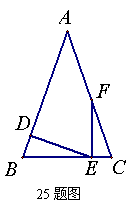
在等腰△ABC中，已知AB=AC=3，，D为AB上一点，过点D作DE⊥AB交BC边于点E，过点E作EF⊥BC交AC边于点F．

（1）当BD长为何值时，以点F为圆心，线段为半径的圆与BC边相切？

（2）过点F作FP⊥AC，与线段DE交于点G，设BD长为，△EFG的面积为，求关于的函数解析式及其定义域．

查看答案和解析>>

科目：czsx 来源：初三奥赛训练题17：几何不等式（解析版） 题型：填空题

在等腰△ABC中，CD是底边AB上的高，E是腰BC的中点，AE与CD交于F，现给出三条路线：
（a）A→F→C→E→B→D→A；
（b）A→C→E→B→D→F→A；
（c）A→D→B→E→F→C→A；
它们的长度分别记为L（a）、L（b）及L（c），则L（a）＜L（b），L（a）＜L（c），L（b）＜L（c）中一定能成立的是．

查看答案和解析>>

科目：czsx 来源：《24.2.1 点和圆的位置关系》2009年同步练习（解析版） 题型：解答题

在等腰△ABC中，B、C为定点，且AC=AB，D为BC的中点，以BC为直径作⊙D，问：（1）顶角A等于多少度时，点A在⊙D上？（2）顶角A等于多少度时，点A在⊙D内部？（3）顶角A等于多少度时，点A在⊙D外部？

查看答案和解析>>

科目：czsx 来源：不详 题型：填空题

在等腰△ABC中，CD是底边AB上的高，E是腰BC的中点，AE与CD交于F，现给出三条路线：
（a）A→F→C→E→B→D→A；
（b）A→C→E→B→D→F→A；
（c）A→D→B→E→F→C→A；
它们的长度分别记为L（a）、L（b）及L（c），则L（a）＜L（b），L（a）＜L（c），L（b）＜L（c）中一定能成立的是______．

查看答案和解析>>

科目：czsx 来源： 题型：

47、在等腰△ABC中，B、C为定点，且AC=AB，D为BC的中点，以BC为直径作⊙D，问：（1）顶角A等于多少度时，点A在⊙D上？（2）顶角A等于多少度时，点A在⊙D内部？（3）顶角A等于多少度时，点A在⊙D外部？

查看答案和解析>>

科目：czsx 来源： 题型：

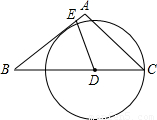
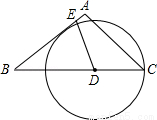
如图，在等腰△ABC中，AB=AC=5，BC=6，点D为BC边上一动点（不与点B重合），过D作射线DE交AB边于E，使∠BDE=∠A，以D为圆心、DC的长为半径作⊙D．
（1）设BD=x，AE=y，求y关于x的函数关系式，并写出定义域．
（2）当⊙D与AB边相切时，求BD的长．
（3）如果⊙E是以E为圆心，AE的长为半径的圆，那么当BD的长为多少时，⊙D与⊙E相切？

查看答案和解析>>

科目：czsx 来源：2013-2014学年上海市普陀区中考二模数学试卷（解析版） 题型：解答题

如图，在等腰△ABC中，AB=AC=5，BC=6，点D为BC边上一动点（不与点B重合），过D作射线DE交AB边于E，使∠BDE=∠A，以D为圆心、DC的长为半径作⊙D．

（1）设BD=x，AE=y，求y关于x的函数关系式，并写出定义域．

（2）当⊙D与AB边相切时，求BD的长．

（3）如果⊙E是以E为圆心，AE的长为半径的圆，那么当BD的长为多少时，⊙D与⊙E相切？

查看答案和解析>>

科目：czsx 来源：2012年上海市中考数学全真模拟试卷（一）（解析版） 题型：解答题

如图，在等腰△ABC中，AB=AC=5，BC=6，点D为BC边上一动点（不与点B重合），过D作射线DE交AB边于E，使∠BDE=∠A，以D为圆心、DC的长为半径作⊙D．
（1）设BD=x，AE=y，求y关于x的函数关系式，并写出定义域．
（2）当⊙D与AB边相切时，求BD的长．
（3）如果⊙E是以E为圆心，AE的长为半径的圆，那么当BD的长为多少时，⊙D与⊙E相切？

查看答案和解析>>

练习册

高中

初中

小学

在等腰△ABC中.B.C为定点答案解析

在等腰△ABC中，B、C为定点，且AC=AB，D为BC的中点，以BC为直径作⊙D，问：
（1）顶角A等于多少度时，点A在⊙D上？（2）顶角A等于多少度时，点A在⊙D内部？（3）顶角A等于多少度时，点A在⊙D外部？