如图.圆o半径为5.点p在圆o外pb角圆o于ab两点答案解析
科目:czsx
来源:
题型:解答题
(1)操作并观察:如图a,两个半径为r的等圆⊙O1与⊙O2外切于点P.将三角板的直角顶点放在点P,再将三角板绕点P旋转,使三角板的两直角边中的一边PA与⊙O1相交于A,另一边PB与⊙O2相交于点B(转动中直角边与两圆都不相切).在转动过程中;线段AB的长与半径r之间有什么关系?请回答并证明你得到的结论;
(2)如图b,设⊙O1与⊙O2外切于点P,半径分别为r1、r2(r1>r2),重复(1)中的操作过程,观察线段AB的长度与r1、r2之间有怎样的关系,并说明理由.
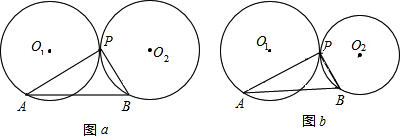
查看答案和解析>>
科目:czsx
来源:
题型:
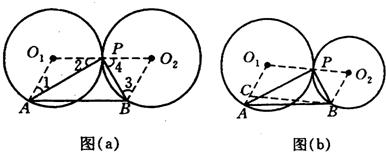
29、(1)操作并观察:如图a,两个半径为r的等圆⊙O
1与⊙O
2外切于点P.将三角板的直角顶点放在点P,再将三角板绕点P旋转,使三角板的两直角边中的一边PA与⊙O
1相交于A,另一边PB与⊙O
2相交于点B(转动中直角边与两圆都不相切).在转动过程中;线段AB的长与半径r之间有什么关系?请回答并证明你得到的结论;
(2)如图b,设⊙O
1与⊙O
2外切于点P,半径分别为r
1、r
2(r
1>r
2),重复(1)中的操作过程,观察线段AB的长度与r
1、r
2之间有怎样的关系,并说明理由.
查看答案和解析>>
科目:czsx
来源:2002年全国中考数学试题汇编《圆》(13)(解析版)
题型:解答题
(2002•太原)(1)操作并观察:如图a,两个半径为r的等圆⊙O
1与⊙O
2外切于点P.将三角板的直角顶点放在点P,再将三角板绕点P旋转,使三角板的两直角边中的一边PA与⊙O
1相交于A,另一边PB与⊙O
2相交于点B(转动中直角边与两圆都不相切).在转动过程中;线段AB的长与半径r之间有什么关系?请回答并证明你得到的结论;
(2)如图b,设⊙O
1与⊙O
2外切于点P,半径分别为r
1、r
2(r
1>r
2),重复(1)中的操作过程,观察线段AB的长度与r
1、r
2之间有怎样的关系,并说明理由.
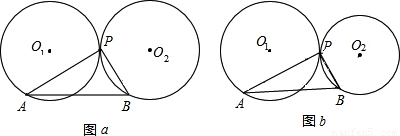
查看答案和解析>>
科目:czsx
来源:2002年山西省太原市中考数学试卷(解析版)
题型:解答题
(2002•太原)(1)操作并观察:如图a,两个半径为r的等圆⊙O
1与⊙O
2外切于点P.将三角板的直角顶点放在点P,再将三角板绕点P旋转,使三角板的两直角边中的一边PA与⊙O
1相交于A,另一边PB与⊙O
2相交于点B(转动中直角边与两圆都不相切).在转动过程中;线段AB的长与半径r之间有什么关系?请回答并证明你得到的结论;
(2)如图b,设⊙O
1与⊙O
2外切于点P,半径分别为r
1、r
2(r
1>r
2),重复(1)中的操作过程,观察线段AB的长度与r
1、r
2之间有怎样的关系,并说明理由.
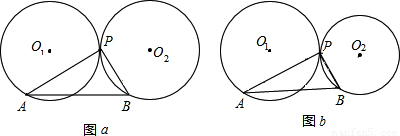
查看答案和解析>>
科目:czsx
来源:
题型:
如图,⊙A和⊙B是外离两圆,⊙A的半径长为2,⊙B的半径长为1,AB=4,P为连接两圆圆心的线段AB上的一点,PC切⊙A于点C,PD切⊙B于点D.
(1)若PC=PD,求PB的长.
(2)试问线段AB上是否存在一点P,使PC
2+PD
2=4?如果存在,问这样的P点有几个并求出PB的值;如果不存在,说明理由.
(3)当点P在线段AB上运动到某处,使PC⊥PD时,就有△APC∽△PBD.请问:除上述情况外,当点P在线段AB上运动到何处(说明PB的长为多少;或PC
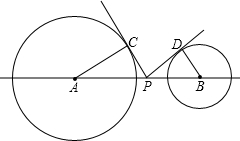
、PD具有何种关系)时,这两个三角形仍相似;并判断此时直线CP与⊙B的位置关系,证明你的结论.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
如图,⊙A和⊙B是外离两圆,⊙A的半径长为2,⊙B的半径长为1,AB=4,P为连接两圆圆心的线段AB上的一点,PC切⊙A于点C,PD切⊙B于点D.
(1)若PC=PD,求PB的长.
(2)试问线段AB上是否存在一点P,使PC2+PD2=4?如果存在,问这样的P点有几个并求出PB的值;如果不存在,说明理由.
(3)当点P在线段AB上运动到某处,使PC⊥PD时,就有△APC∽△PBD.请问:除上述情况外,当点P在线段AB上运动到何处(说明PB的长为多少;或PC 、PD具有何种关系)时,这两个三角形仍相似;并判断此时直线CP与⊙B的位置关系,证明你的结论.
、PD具有何种关系)时,这两个三角形仍相似;并判断此时直线CP与⊙B的位置关系,证明你的结论.
查看答案和解析>>
科目:czsx
来源:2003年全国中考数学试题汇编《图形的相似》(04)(解析版)
题型:解答题
(2003•舟山)如图,⊙A和⊙B是外离两圆,⊙A的半径长为2,⊙B的半径长为1,AB=4,P为连接两圆圆心的线段AB上的一点,PC切⊙A于点C,PD切⊙B于点D.
(1)若PC=PD,求PB的长.
(2)试问线段AB上是否存在一点P,使PC
2+PD
2=4?如果存在,问这样的P点有几个并求出PB的值;如果不存在,说明理由.
(3)当点P在线段AB上运动到某处,使PC⊥PD时,就有△APC∽△PBD.请问:除上述情况外,当点P在线段AB上运动到何处(说明PB的长为多少;或PC、PD具有何种关系)时,这两个三角形仍相似;并判断此时直线CP与⊙B的位置关系,证明你的结论.
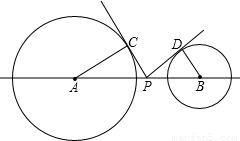
查看答案和解析>>
科目:czsx
来源:2003年全国中考数学试题汇编《圆》(10)(解析版)
题型:解答题
(2003•舟山)如图,⊙A和⊙B是外离两圆,⊙A的半径长为2,⊙B的半径长为1,AB=4,P为连接两圆圆心的线段AB上的一点,PC切⊙A于点C,PD切⊙B于点D.
(1)若PC=PD,求PB的长.
(2)试问线段AB上是否存在一点P,使PC
2+PD
2=4?如果存在,问这样的P点有几个并求出PB的值;如果不存在,说明理由.
(3)当点P在线段AB上运动到某处,使PC⊥PD时,就有△APC∽△PBD.请问:除上述情况外,当点P在线段AB上运动到何处(说明PB的长为多少;或PC、PD具有何种关系)时,这两个三角形仍相似;并判断此时直线CP与⊙B的位置关系,证明你的结论.

查看答案和解析>>
科目:czsx
来源:2003年全国中考数学试题汇编《三角形》(08)(解析版)
题型:解答题
(2003•舟山)如图,⊙A和⊙B是外离两圆,⊙A的半径长为2,⊙B的半径长为1,AB=4,P为连接两圆圆心的线段AB上的一点,PC切⊙A于点C,PD切⊙B于点D.
(1)若PC=PD,求PB的长.
(2)试问线段AB上是否存在一点P,使PC
2+PD
2=4?如果存在,问这样的P点有几个并求出PB的值;如果不存在,说明理由.
(3)当点P在线段AB上运动到某处,使PC⊥PD时,就有△APC∽△PBD.请问:除上述情况外,当点P在线段AB上运动到何处(说明PB的长为多少;或PC、PD具有何种关系)时,这两个三角形仍相似;并判断此时直线CP与⊙B的位置关系,证明你的结论.

查看答案和解析>>
科目:czsx
来源:2003年全国中考数学试题汇编《一元二次方程》(06)(解析版)
题型:解答题
(2003•舟山)如图,⊙A和⊙B是外离两圆,⊙A的半径长为2,⊙B的半径长为1,AB=4,P为连接两圆圆心的线段AB上的一点,PC切⊙A于点C,PD切⊙B于点D.
(1)若PC=PD,求PB的长.
(2)试问线段AB上是否存在一点P,使PC
2+PD
2=4?如果存在,问这样的P点有几个并求出PB的值;如果不存在,说明理由.
(3)当点P在线段AB上运动到某处,使PC⊥PD时,就有△APC∽△PBD.请问:除上述情况外,当点P在线段AB上运动到何处(说明PB的长为多少;或PC、PD具有何种关系)时,这两个三角形仍相似;并判断此时直线CP与⊙B的位置关系,证明你的结论.

查看答案和解析>>
科目:czsx
来源:2003年浙江省舟山市中考数学试卷(解析版)
题型:解答题
(2003•舟山)如图,⊙A和⊙B是外离两圆,⊙A的半径长为2,⊙B的半径长为1,AB=4,P为连接两圆圆心的线段AB上的一点,PC切⊙A于点C,PD切⊙B于点D.
(1)若PC=PD,求PB的长.
(2)试问线段AB上是否存在一点P,使PC
2+PD
2=4?如果存在,问这样的P点有几个并求出PB的值;如果不存在,说明理由.
(3)当点P在线段AB上运动到某处,使PC⊥PD时,就有△APC∽△PBD.请问:除上述情况外,当点P在线段AB上运动到何处(说明PB的长为多少;或PC、PD具有何种关系)时,这两个三角形仍相似;并判断此时直线CP与⊙B的位置关系,证明你的结论.
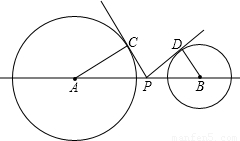
查看答案和解析>>

![]() O1与
O1与![]() O2外切于点P,将三角板的直角顶点放在点P,再将三角板绕点P旋转,使三角板的两直角边中的一边PA与
O2外切于点P,将三角板的直角顶点放在点P,再将三角板绕点P旋转,使三角板的两直角边中的一边PA与![]() O1相交于A,另一边PB与
O1相交于A,另一边PB与![]() O2相交于B(转动中直角边与两圆都不相切),在转动过程中,线段AB的长与半径r之间有什么关系?请说明理由.
O2相交于B(转动中直角边与两圆都不相切),在转动过程中,线段AB的长与半径r之间有什么关系?请说明理由.
![]() O1与
O1与![]() O2的半径不相等,
O2的半径不相等,![]() O1与
O1与![]() O2仍是外切于点P.设
O2仍是外切于点P.设![]() O1的半径为R,
O1的半径为R,![]() O2的半径为r(R>r),重复(1)中的操作过程,观察并分析线段AB与R、r之间有怎样的关系,并说明理由.
O2的半径为r(R>r),重复(1)中的操作过程,观察并分析线段AB与R、r之间有怎样的关系,并说明理由.
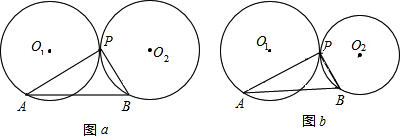

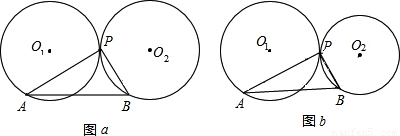
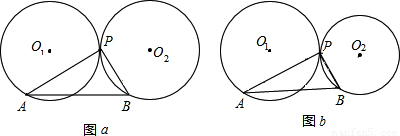
 、PD具有何种关系)时,这两个三角形仍相似;并判断此时直线CP与⊙B的位置关系,证明你的结论.
、PD具有何种关系)时,这两个三角形仍相似;并判断此时直线CP与⊙B的位置关系,证明你的结论.  、PD具有何种关系)时,这两个三角形仍相似;并判断此时直线CP与⊙B的位置关系,证明你的结论.
、PD具有何种关系)时,这两个三角形仍相似;并判断此时直线CP与⊙B的位置关系,证明你的结论.



