如图.已知抛物线y=-x-2x+a与y轴相交于点A.顶点为M答案解析
科目:czsx
来源:
题型:
已知抛物线y=x
2-2x+a(a<0)与y轴相交于点A,顶点为M.直线y=
x-a分别与x轴,y轴相交于B,C两点,并且与直线AM相交于点N.
(1)试用含a的代数式分别表示点M与N的坐标;
(2)如图,将△NAC沿y轴翻折,若点N的对应点N′恰好落在抛物线上,AN′与x轴交于点D,连接CD,求a的值和四边形ADCN的面积;
(3)在抛物线y=x
2-2x+a(a<0)上是否存在一点P,使得以P,A,C,N为顶点的四边形是平行四边形?若存在,求出P点的坐标;若不存在,试说明理由.

查看答案和解析>>
科目:czsx
来源:
题型:
已知抛物线y=-x
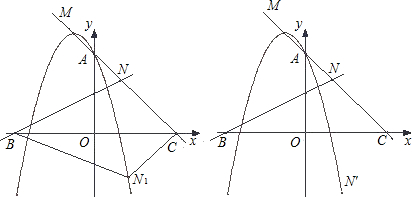
2-2x+a(a>0)与y轴相交于点A,顶点为M.直线y=
x+a与x轴相交于B点,与直线AM相交于N点;直线AM与x轴相交于C点
(1)求M的坐标与MA的解析式(用字母a表示);
(2)如图,将△NBC沿x轴翻折,若N点的对应点N′恰好落在抛物线上,求a的值;
(3)在抛物线y=-x
2-2x+a(a>0)上是否存在一点P,使得以P、B、C、N为顶点的四边形是平行四边形?若存在,求出a的值;若不存在,说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:044
已知抛物线 与x轴相交于A、B两点(A点在B点的左侧),顶点为P.
与x轴相交于A、B两点(A点在B点的左侧),顶点为P.
(1)求A、B、P三点的坐标;
(2)在如图所示的直角坐标系内画出此抛物线的简图并根据简图,写出当x取何值时,函数值y大于零;

(3)确定此抛物线与直线y=-2x+6公共点的个数,并说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
已知抛物线y=-x2-2x+a(a>0)与y轴相交于点A,顶点为M.直线y=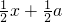 与x轴相交于B点,与直线AM相交于N点;直线AM与x轴相交于C点
与x轴相交于B点,与直线AM相交于N点;直线AM与x轴相交于C点
(1)求M的坐标与MA的解析式(用字母a表示);
(2)如图,将△NBC沿x轴翻折,若N点的对应点N′恰好落在抛物线上,求a的值;
(3)在抛物线y=-x2-2x+a(a>0)上是否存在一点P,使得以P、B、C、N为顶点的四边形是平行四边形?若存在,求出a的值;若不存在,说明理由.

查看答案和解析>>
科目:czsx
来源:福建省模拟题
题型:解答题
已知抛物线y=x
2-2x+a(a<0)与y轴相交于点A,顶点为M,直线
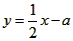
分别与x轴,y轴相交于B,C两点,并且与直线AM相交于点N。
(1)试用含a的代数式分别表示点M与N的坐标;
(2)如图,将△NAC沿y轴翻折,若点N的对应点N′恰好落在抛物线上,AN′与x轴交于点D,连接CD,求:①a的值;
②四边形ADCN的面积;
(3)在抛物线y=x
2-2x+a(a<0)上是否存在一点P,使得以P,A,C,N为顶点的四边形是平行四边形?若存在,求出P点的坐标;若不存在,试说明理由。
查看答案和解析>>
科目:czsx
来源:第2章《二次函数》中考题集(32):2.7 最大面积是多少(解析版)
题型:解答题
已知抛物线y=x
2-2x+a(a<0)与y轴相交于点A,顶点为M.直线y=

x-a分别与x轴,y轴相交于B,C两点,并且与直线AM相交于点N.
(1)试用含a的代数式分别表示点M与N的坐标;
(2)如图,将△NAC沿y轴翻折,若点N的对应点N′恰好落在抛物线上,AN′与x轴交于点D,连接CD,求a的值和四边形ADCN的面积;
(3)在抛物线y=x
2-2x+a(a<0)上是否存在一点P,使得以P,A,C,N为顶点的四边形是平行四边形?若存在,求出P点的坐标;若不存在,试说明理由.

查看答案和解析>>
科目:czsx
来源:第34章《二次函数》中考题集(35):34.4 二次函数的应用(解析版)
题型:解答题
已知抛物线y=x
2-2x+a(a<0)与y轴相交于点A,顶点为M.直线y=

x-a分别与x轴,y轴相交于B,C两点,并且与直线AM相交于点N.
(1)试用含a的代数式分别表示点M与N的坐标;
(2)如图,将△NAC沿y轴翻折,若点N的对应点N′恰好落在抛物线上,AN′与x轴交于点D,连接CD,求a的值和四边形ADCN的面积;
(3)在抛物线y=x
2-2x+a(a<0)上是否存在一点P,使得以P,A,C,N为顶点的四边形是平行四边形?若存在,求出P点的坐标;若不存在,试说明理由.

查看答案和解析>>
科目:czsx
来源:第26章《二次函数》中考题集(33):26.3 实际问题与二次函数(解析版)
题型:解答题
已知抛物线y=x
2-2x+a(a<0)与y轴相交于点A,顶点为M.直线y=

x-a分别与x轴,y轴相交于B,C两点,并且与直线AM相交于点N.
(1)试用含a的代数式分别表示点M与N的坐标;
(2)如图,将△NAC沿y轴翻折,若点N的对应点N′恰好落在抛物线上,AN′与x轴交于点D,连接CD,求a的值和四边形ADCN的面积;
(3)在抛物线y=x
2-2x+a(a<0)上是否存在一点P,使得以P,A,C,N为顶点的四边形是平行四边形?若存在,求出P点的坐标;若不存在,试说明理由.

查看答案和解析>>
科目:czsx
来源:2009-2010学年江苏省泰州市姜堰市九年级(下)期中数学试卷(解析版)
题型:解答题
已知抛物线y=-x
2-2x+a(a>0)与y轴相交于点A,顶点为M.直线y=

与x轴相交于B点,与直线AM相交于N点;直线AM与x轴相交于C点
(1)求M的坐标与MA的解析式(用字母a表示);
(2)如图,将△NBC沿x轴翻折,若N点的对应点N′恰好落在抛物线上,求a的值;
(3)在抛物线y=-x
2-2x+a(a>0)上是否存在一点P,使得以P、B、C、N为顶点的四边形是平行四边形?若存在,求出a的值;若不存在,说明理由.

查看答案和解析>>
科目:czsx
来源:2011-2012学年湖北省黄冈市团风县九年级(上)期末数学试卷(解析版)
题型:解答题
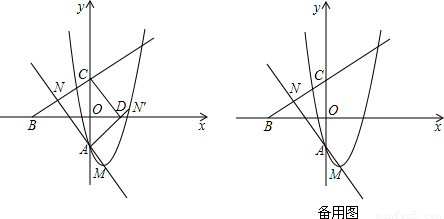
已知抛物线y=x
2-2x+a(a<0)与y轴相交于点A,顶点为M.直线y=

x-a分别与x轴,y轴相交于B,C两点,并且与直线AM相交于点N.
(1)试用含a的代数式分别表示点M与N的坐标;
(2)如图,将△NAC沿y轴翻折,若点N的对应点N′恰好落在抛物线上,AN′与x轴交于点D,连接CD,求a的值和四边形ADCN的面积;
(3)在抛物线y=x
2-2x+a(a<0)上是否存在一点P,使得以P,A,C,N为顶点的四边形是平行四边形?若存在,求出P点的坐标;若不存在,试说明理由.
查看答案和解析>>
科目:czsx
来源:2011-2012学年北京市海淀区九年级(上)第二次月考数学试卷(解析版)
题型:解答题
已知抛物线y=x
2-2x+a(a<0)与y轴相交于点A,顶点为M.直线y=

x-a分别与x轴,y轴相交于B,C两点,并且与直线AM相交于点N.
(1)试用含a的代数式分别表示点M与N的坐标;
(2)如图,将△NAC沿y轴翻折,若点N的对应点N′恰好落在抛物线上,AN′与x轴交于点D,连接CD,求a的值和四边形ADCN的面积;
(3)在抛物线y=x
2-2x+a(a<0)上是否存在一点P,使得以P,A,C,N为顶点的四边形是平行四边形?若存在,求出P点的坐标;若不存在,试说明理由.

查看答案和解析>>
科目:czsx
来源:2010年浙江省嘉兴市桐乡市九年级文理科联赛模拟试卷(07)(解析版)
题型:解答题
已知抛物线y=x
2-2x+a(a<0)与y轴相交于点A,顶点为M.直线y=

x-a分别与x轴,y轴相交于B,C两点,并且与直线AM相交于点N.
(1)试用含a的代数式分别表示点M与N的坐标;
(2)如图,将△NAC沿y轴翻折,若点N的对应点N′恰好落在抛物线上,AN′与x轴交于点D,连接CD,求a的值和四边形ADCN的面积;
(3)在抛物线y=x
2-2x+a(a<0)上是否存在一点P,使得以P,A,C,N为顶点的四边形是平行四边形?若存在,求出P点的坐标;若不存在,试说明理由.

查看答案和解析>>
科目:czsx
来源:第2章《二次函数》中考题集(36):2.8 二次函数的应用(解析版)
题型:解答题
已知抛物线y=x
2-2x+a(a<0)与y轴相交于点A,顶点为M.直线y=

x-a分别与x轴,y轴相交于B,C两点,并且与直线AM相交于点N.
(1)试用含a的代数式分别表示点M与N的坐标;
(2)如图,将△NAC沿y轴翻折,若点N的对应点N′恰好落在抛物线上,AN′与x轴交于点D,连接CD,求a的值和四边形ADCN的面积;
(3)在抛物线y=x
2-2x+a(a<0)上是否存在一点P,使得以P,A,C,N为顶点的四边形是平行四边形?若存在,求出P点的坐标;若不存在,试说明理由.

查看答案和解析>>
科目:czsx
来源:第20章《二次函数和反比例函数》中考题集(32):20.5 二次函数的一些应用(解析版)
题型:解答题
已知抛物线y=x
2-2x+a(a<0)与y轴相交于点A,顶点为M.直线y=

x-a分别与x轴,y轴相交于B,C两点,并且与直线AM相交于点N.
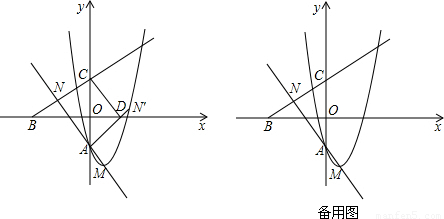
(1)试用含a的代数式分别表示点M与N的坐标;
(2)如图,将△NAC沿y轴翻折,若点N的对应点N′恰好落在抛物线上,AN′与x轴交于点D,连接CD,求a的值和四边形ADCN的面积;
(3)在抛物线y=x
2-2x+a(a<0)上是否存在一点P,使得以P,A,C,N为顶点的四边形是平行四边形?若存在,求出P点的坐标;若不存在,试说明理由.
查看答案和解析>>
科目:czsx
来源:第2章《二次函数》中考题集(33):2.4 二次函数的应用(解析版)
题型:解答题
已知抛物线y=x
2-2x+a(a<0)与y轴相交于点A,顶点为M.直线y=

x-a分别与x轴,y轴相交于B,C两点,并且与直线AM相交于点N.
(1)试用含a的代数式分别表示点M与N的坐标;
(2)如图,将△NAC沿y轴翻折,若点N的对应点N′恰好落在抛物线上,AN′与x轴交于点D,连接CD,求a的值和四边形ADCN的面积;
(3)在抛物线y=x
2-2x+a(a<0)上是否存在一点P,使得以P,A,C,N为顶点的四边形是平行四边形?若存在,求出P点的坐标;若不存在,试说明理由.

查看答案和解析>>
科目:czsx
来源:第23章《二次函数与反比例函数》中考题集(32):23.5 二次函数的应用(解析版)
题型:解答题
已知抛物线y=x
2-2x+a(a<0)与y轴相交于点A,顶点为M.直线y=

x-a分别与x轴,y轴相交于B,C两点,并且与直线AM相交于点N.
(1)试用含a的代数式分别表示点M与N的坐标;
(2)如图,将△NAC沿y轴翻折,若点N的对应点N′恰好落在抛物线上,AN′与x轴交于点D,连接CD,求a的值和四边形ADCN的面积;
(3)在抛物线y=x
2-2x+a(a<0)上是否存在一点P,使得以P,A,C,N为顶点的四边形是平行四边形?若存在,求出P点的坐标;若不存在,试说明理由.

查看答案和解析>>
科目:czsx
来源:2011年浙江省杭州市江干区中考数学模拟试卷(解析版)
题型:解答题
已知抛物线y=x
2-2x+a(a<0)与y轴相交于点A,顶点为M.直线y=

x-a分别与x轴,y轴相交于B,C两点,并且与直线AM相交于点N.
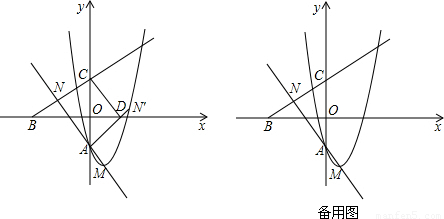
(1)试用含a的代数式分别表示点M与N的坐标;
(2)如图,将△NAC沿y轴翻折,若点N的对应点N′恰好落在抛物线上,AN′与x轴交于点D,连接CD,求a的值和四边形ADCN的面积;
(3)在抛物线y=x
2-2x+a(a<0)上是否存在一点P,使得以P,A,C,N为顶点的四边形是平行四边形?若存在,求出P点的坐标;若不存在,试说明理由.
查看答案和解析>>
科目:czsx
来源:2012年中考数学模拟卷试卷(三十四)(解析版)
题型:解答题
已知抛物线y=x
2-2x+a(a<0)与y轴相交于点A,顶点为M.直线y=

x-a分别与x轴,y轴相交于B,C两点,并且与直线AM相交于点N.
(1)试用含a的代数式分别表示点M与N的坐标;
(2)如图,将△NAC沿y轴翻折,若点N的对应点N′恰好落在抛物线上,AN′与x轴交于点D,连接CD,求a的值和四边形ADCN的面积;
(3)在抛物线y=x
2-2x+a(a<0)上是否存在一点P,使得以P,A,C,N为顶点的四边形是平行四边形?若存在,求出P点的坐标;若不存在,试说明理由.

查看答案和解析>>
科目:czsx
来源:2011年福建省泉州市中考数学模拟试卷(二)(解析版)
题型:解答题
已知抛物线y=x
2-2x+a(a<0)与y轴相交于点A,顶点为M.直线y=

x-a分别与x轴,y轴相交于B,C两点,并且与直线AM相交于点N.
(1)试用含a的代数式分别表示点M与N的坐标;
(2)如图,将△NAC沿y轴翻折,若点N的对应点N′恰好落在抛物线上,AN′与x轴交于点D,连接CD,求a的值和四边形ADCN的面积;
(3)在抛物线y=x
2-2x+a(a<0)上是否存在一点P,使得以P,A,C,N为顶点的四边形是平行四边形?若存在,求出P点的坐标;若不存在,试说明理由.

查看答案和解析>>
科目:czsx
来源:2011年北京市延庆县中考数学二模试卷(解析版)
题型:解答题
已知抛物线y=x
2-2x+a(a<0)与y轴相交于点A,顶点为M.直线y=

x-a分别与x轴,y轴相交于B,C两点,并且与直线AM相交于点N.
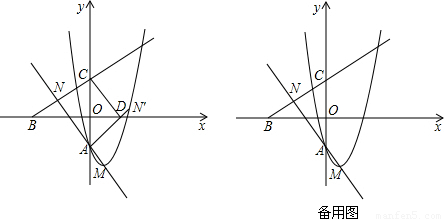
(1)试用含a的代数式分别表示点M与N的坐标;
(2)如图,将△NAC沿y轴翻折,若点N的对应点N′恰好落在抛物线上,AN′与x轴交于点D,连接CD,求a的值和四边形ADCN的面积;
(3)在抛物线y=x
2-2x+a(a<0)上是否存在一点P,使得以P,A,C,N为顶点的四边形是平行四边形?若存在,求出P点的坐标;若不存在,试说明理由.
查看答案和解析>>



![]() 与x轴相交于A、B两点(A点在B点的左侧),顶点为P.
与x轴相交于A、B两点(A点在B点的左侧),顶点为P.
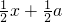 与x轴相交于B点,与直线AM相交于N点;直线AM与x轴相交于C点
与x轴相交于B点,与直线AM相交于N点;直线AM与x轴相交于C点
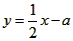 分别与x轴,y轴相交于B,C两点,并且与直线AM相交于点N。
分别与x轴,y轴相交于B,C两点,并且与直线AM相交于点N。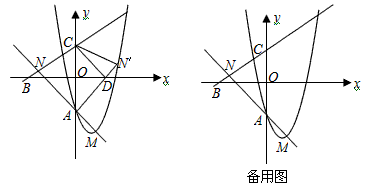
 x-a分别与x轴,y轴相交于B,C两点,并且与直线AM相交于点N.
x-a分别与x轴,y轴相交于B,C两点,并且与直线AM相交于点N.
 x-a分别与x轴,y轴相交于B,C两点,并且与直线AM相交于点N.
x-a分别与x轴,y轴相交于B,C两点,并且与直线AM相交于点N.
 x-a分别与x轴,y轴相交于B,C两点,并且与直线AM相交于点N.
x-a分别与x轴,y轴相交于B,C两点,并且与直线AM相交于点N.
 与x轴相交于B点,与直线AM相交于N点;直线AM与x轴相交于C点
与x轴相交于B点,与直线AM相交于N点;直线AM与x轴相交于C点
 x-a分别与x轴,y轴相交于B,C两点,并且与直线AM相交于点N.
x-a分别与x轴,y轴相交于B,C两点,并且与直线AM相交于点N.
 x-a分别与x轴,y轴相交于B,C两点,并且与直线AM相交于点N.
x-a分别与x轴,y轴相交于B,C两点,并且与直线AM相交于点N.
 x-a分别与x轴,y轴相交于B,C两点,并且与直线AM相交于点N.
x-a分别与x轴,y轴相交于B,C两点,并且与直线AM相交于点N.
 x-a分别与x轴,y轴相交于B,C两点,并且与直线AM相交于点N.
x-a分别与x轴,y轴相交于B,C两点,并且与直线AM相交于点N.
 x-a分别与x轴,y轴相交于B,C两点,并且与直线AM相交于点N.
x-a分别与x轴,y轴相交于B,C两点,并且与直线AM相交于点N.
 x-a分别与x轴,y轴相交于B,C两点,并且与直线AM相交于点N.
x-a分别与x轴,y轴相交于B,C两点,并且与直线AM相交于点N.
 x-a分别与x轴,y轴相交于B,C两点,并且与直线AM相交于点N.
x-a分别与x轴,y轴相交于B,C两点,并且与直线AM相交于点N.
 x-a分别与x轴,y轴相交于B,C两点,并且与直线AM相交于点N.
x-a分别与x轴,y轴相交于B,C两点,并且与直线AM相交于点N.
 x-a分别与x轴,y轴相交于B,C两点,并且与直线AM相交于点N.
x-a分别与x轴,y轴相交于B,C两点,并且与直线AM相交于点N.
 x-a分别与x轴,y轴相交于B,C两点,并且与直线AM相交于点N.
x-a分别与x轴,y轴相交于B,C两点,并且与直线AM相交于点N.
 x-a分别与x轴,y轴相交于B,C两点,并且与直线AM相交于点N.
x-a分别与x轴,y轴相交于B,C两点,并且与直线AM相交于点N.