解:(1)已知抛物线:y=-x
2-2x+a=-(x+1)
2+a+1;
∴M(-1,a+1),
易知:A(0,a),设直线MA的解析式为y=kx+b,则有:

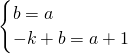
,
解得
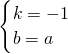
,
∴直线MA:y=-x+a;
(2)联立直线MA、直线BN的解析式有:
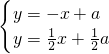
,
解得
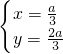
故N(

,

a);
由题意知:N、N′关于x轴对称,那么N′(

,-

);
若点N′在抛物线的图象上,则有:
-(

)
2-

+a=-

,
解得a=9.
故点N′恰好落在抛物线上时,a=9;
(3)分别过B、C、N作NC、BN、BC的平行线(如图),则四边形BP
1CN、四边形BCP
2N、四边形BCNP
3都是平行四边形;
易知B(-a,0),C(a,0),N(

,

);
故P
1(-

a,-

a),P
2(

a,

a),
P
3(-

a,

a);
把P
1代入抛物线的解析式中,得:
-(-

a)
2-2(-

a)+a=-

a,
解得a=21;
把P
2代入抛物线的解析式中,得:
-(

a)
2-2×

a+a=

a,
解得a=-

;
由于a>0,
故此种情况不成立;
把P
3代入抛物线的解析式中,得:
-(-

a)
2-2(-

a)+a=

a,
解得a=
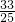
;
综上所述,存在符合条件的P点,且此时a的值为:a
1=
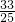
,a
2=21.
分析:(1)将抛物线的解析式化为顶点坐标式,即可求得点M的坐标;易知点A坐标为(0,a),利用待定系数法即可求得直线MA的解析式;
(2)联立直线MA、直线BN的解析式,即可求得点N的坐标,由于点N、N′关于x轴对称,那么它们的横坐标相同,纵坐标互为相反数,由此可求得点N′的坐标,再将其代入抛物线的解析式中,即可求得a的值;
(3)分别过B、C、N作NC、BN、BC的平行线,三线相交于P
1、P
2、P
3三点,则四边形BP
1CN、四边形BCP
2N、四边形BCNP
3都是平行四边形,易求得B、C的坐标,根据平行四边形的性质即可得到P
1、P
2、P
3的坐标,然后将它们分别代入抛物线的解析式中,即可求得a的值.
点评:此题考查了一次函数解析式的确定、关于x轴对称的点的坐标特征、函数图象上的点的坐标意义以及平行四边形的判定和性质等知识.(3)题中,一定要把所有的情况都考虑到,做到不漏解.

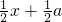 与x轴相交于B点,与直线AM相交于N点;直线AM与x轴相交于C点
与x轴相交于B点,与直线AM相交于N点;直线AM与x轴相交于C点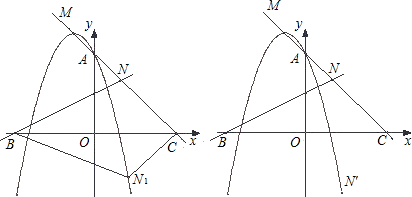

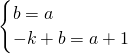 ,
,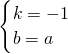 ,
,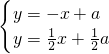 ,
,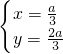
 ,
, a);
a); ,-
,- );
); )2-
)2- +a=-
+a=- ,
, ,
, );
); a,-
a,- a),P2(
a),P2( a,
a, a),
a), a,
a, a);
a); a)2-2(-
a)2-2(- a)+a=-
a)+a=- a,
a, a)2-2×
a)2-2× a+a=
a+a= a,
a, ;
; a)2-2(-
a)2-2(- a)+a=
a)+a= a,
a,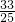 ;
;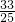 ,a2=21.
,a2=21.

 (1)求b+c的值;
(1)求b+c的值; (2012•虹口区一模)如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx+c经过A(0,3),B(1,0)两点,顶点为M.
(2012•虹口区一模)如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx+c经过A(0,3),B(1,0)两点,顶点为M.