在三角形ABC中.角ACB=90度.AC=BC,直线l经过答案解析
科目:czsx
来源:
题型:
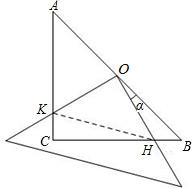
在△ABC中,∠ACB=90°,AC=BC=4,现将一块边长足够大的直角三角板的直角顶点置于AB的中点O,两直角边分别经过点B、C,然后将三角板绕点O按顺时针方向旋转一个角度α(0°<α<90°),旋转后,直角三角板的直角边分别与AC、BC相交于点K、H,四边形CHOK是旋转过程中三角板与△ABC的重叠部分(如图所示),那么,在上述旋转过程中:
(1)线段BH与CK具有怎样的数量关系?四边形CHOK的面积是否发生变化?证明你发现的结论;
(2)连接HK,设BH=x.当△CKH的面积为
时,求出x的值.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
 在△ABC中,∠ACB=90°,AC=BC=4,现将一块边长足够大的直角三角板的直角顶点置于AB的中点O,两直角边分别经过点B、C,然后将三角板绕点O按顺时针方向旋转一个角度α(0°<α<90°),旋转后,直角三角板的直角边分别与AC、BC相交于点K、H,四边形CHOK是旋转过程中三角板与△ABC的重叠部分(如图所示),那么,在上述旋转过程中:
在△ABC中,∠ACB=90°,AC=BC=4,现将一块边长足够大的直角三角板的直角顶点置于AB的中点O,两直角边分别经过点B、C,然后将三角板绕点O按顺时针方向旋转一个角度α(0°<α<90°),旋转后,直角三角板的直角边分别与AC、BC相交于点K、H,四边形CHOK是旋转过程中三角板与△ABC的重叠部分(如图所示),那么,在上述旋转过程中:
(1)线段BH与CK具有怎样的数量关系?四边形CHOK的面积是否发生变化?证明你发现的结论;
(2)连接HK,设BH=x.当△CKH的面积为 时,求出x的值.
时,求出x的值.
查看答案和解析>>
科目:czsx
来源:
题型:

已知在△ABC中,∠ACB=90°,AC=BC=4,现将一块边长足够大的直角三角板的直角顶点置于AB的中点O,两直角边分别经过点B、C,然后将三角板绕点O按顺时针方向旋转一个角度α(0°<α<90°),旋转后,直角三角板的直角边分别与AC、BC相交于点K、H,四边形CHOK是旋转过程中三角板与△ABC的重叠部分(如图所示).那么,在上述旋转过程中:
(1)线段BH与CK具有怎样的数量关系?四边形CHOK的面积是否发生变化?证明你发现的结论;
(2)连接HK,设BH=x.
①当△CHK的面积为
时,求出x的值.
②试问△OHK的面积是否存在最小值,若存在,求出此时x的值,若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
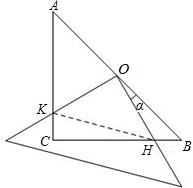 已知在△ABC中,∠ACB=90°,AC=BC=4,现将一块边长足够大的直角三角板的直角顶点置于AB的中点O,两直角边分别经过点B、C,然后将三角板绕点O按顺时针方向旋转一个角度α(0°<α<90°),旋转后,直角三角板的直角边分别与AC、BC相交于点K、H,四边形CHOK是旋转过程中三角板与△ABC的重叠部分(如图所示).那么,在上述旋转过程中:
已知在△ABC中,∠ACB=90°,AC=BC=4,现将一块边长足够大的直角三角板的直角顶点置于AB的中点O,两直角边分别经过点B、C,然后将三角板绕点O按顺时针方向旋转一个角度α(0°<α<90°),旋转后,直角三角板的直角边分别与AC、BC相交于点K、H,四边形CHOK是旋转过程中三角板与△ABC的重叠部分(如图所示).那么,在上述旋转过程中:
(1)线段BH与CK具有怎样的数量关系?四边形CHOK的面积是否发生变化?证明你发现的结论;
(2)连接HK,设BH=x.
①当△CHK的面积为 时,求出x的值.
时,求出x的值.
②试问△OHK的面积是否存在最小值,若存在,求出此时x的值,若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:2012年浙江省省一级重点中学自主招生考试数学模拟试卷(解析版)
题型:解答题
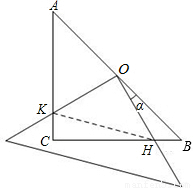
已知在△ABC中,∠ACB=90°,AC=BC=4,现将一块边长足够大的直角三角板的直角顶点置于AB的中点O,两直角边分别经过点B、C,然后将三角板绕点O按顺时针方向旋转一个角度α(0°<α<90°),旋转后,直角三角板的直角边分别与AC、BC相交于点K、H,四边形CHOK是旋转过程中三角板与△ABC的重叠部分(如图所示).那么,在上述旋转过程中:
(1)线段BH与CK具有怎样的数量关系?四边形CHOK的面积是否发生变化?证明你发现的结论;
(2)连接HK,设BH=x.
①当△CHK的面积为

时,求出x的值.
②试问△OHK的面积是否存在最小值,若存在,求出此时x的值,若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
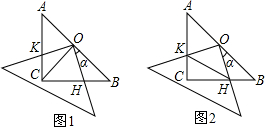
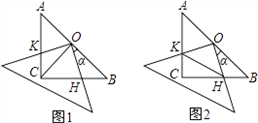
已知:在△ABC中,∠ACB=90°,AC=BC,现将一块边长足够大的直角三角板的直角顶点置于AB的中点O处,两直角边分别经过点B、C,然后将三角板绕点O按顺时针方向旋转一个角度反(0°<a<90°),旋转后,直角三角板的直角边分别与AC、BC相交于点K、H,四边形CHOK是旋转过程中三角板与△ABC的重叠部分(如图1所示).那么,在上述旋转过程中:
(1)如图1,线段BH与CK具有怎样的数量关系?四边形CHOK的面积是否发生变化?请说明你发现的结论的理由.
(2)如图2,连接HK,
①若AK=12,BH=5,求△OKH的面积;
②若AC=BC=4,设BH=x,当△CKH的面积为2时,求x的值,并说出此时四边形CHOK是什么特殊四边形.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
已知:在△ABC中,∠ACB=90°,AC=BC,现将一块边长足够大的直角三角板的直角顶点置于AB的中点O处,两直角边分别经过点B、C,然后将三角板绕点O按顺时针方向旋转一个角度反(0°<a<90°),旋转后,直角三角板的直角边分别与AC、BC相交于点K、H,四边形CHOK是旋转过程中三角板与△ABC的重叠部分(如图1所示).那么,在上述旋转过程中:
(1)如图1,线段BH与CK具有怎样的数量关系?四边形CHOK的面积是否发生变化?请说明你发现的结论的理由.
(2)如图2,连接HK,
①若AK=12,BH=5,求△OKH的面积;
②若AC=BC=4,设BH=x,当△CKH的面积为2时,求x的值,并说出此时四边形CHOK是什么特殊四边形.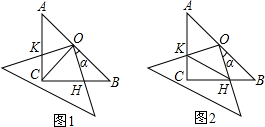
查看答案和解析>>
科目:czsx
来源:四川省期中题
题型:解答题
已知:在△ABC中,∠ACB=90°,AC=BC,现将一块边长足够大的直角三角板的直角顶点置于AB的中点D处,两直角边分别经过点B、C,然后将三角板绕点D按顺时针方向旋转一个角度α(0°<a<90°),旋转后,直角三角板的直角边分别与AC、BC相交于点K、H,四边形CHOK是旋转过程中三角板与△ABC的重叠部分(如图1所示).那么,在上述旋转过程中:
(1)如图1,线段BH与CK具有怎样的数量关系?四边形CHOK的面积是否发生变化?请说明你发现的结论的理由.
(2)如图2,连接HK,
①若AK=12,BH=5,求△OKH的面积;
②若AC=BC=4,设BH=x,当△CKH的面积为2时,求x的值,并说出此时四边形CHOK是什么特殊四边形.
查看答案和解析>>
科目:czsx
来源:2010年甘肃省定西市安定区新集初中九年级数学竞赛试卷(解析版)
题型:解答题
已知:在△ABC中,∠ACB=90°,AC=BC,现将一块边长足够大的直角三角板的直角顶点置于AB的中点O处,两直角边分别经过点B、C,然后将三角板绕点O按顺时针方向旋转一个角度反(0°<a<90°),旋转后,直角三角板的直角边分别与AC、BC相交于点K、H,四边形CHOK是旋转过程中三角板与△ABC的重叠部分(如图1所示).那么,在上述旋转过程中:
(1)如图1,线段BH与CK具有怎样的数量关系?四边形CHOK的面积是否发生变化?请说明你发现的结论的理由.
(2)如图2,连接HK,
①若AK=12,BH=5,求△OKH的面积;
②若AC=BC=4,设BH=x,当△CKH的面积为2时,求x的值,并说出此时四边形CHOK是什么特殊四边形.

查看答案和解析>>
科目:czsx
来源:不详
题型:解答题
已知:在△ABC中,∠ACB=90°,AC=BC,现将一块边长足够大的直角三角板的直角顶点置于AB的中点O处,两直角边分别经过点B、C,然后将三角板绕点O按顺时针方向旋转一个角度反(0°<a<90°),旋转后,直角三角板的直角边分别与AC、BC相交于点K、H,四边形CHOK是旋转过程中三角板与△ABC的重叠部分(如图1所示).那么,在上述旋转过程中:
(1)如图1,线段BH与CK具有怎样的数量关系?四边形CHOK的面积是否发生变化?请说明你发现的结论的理由.
(2)如图2,连接HK,
①若AK=12,BH=5,求△OKH的面积;
②若AC=BC=4,设BH=x,当△CKH的面积为2时,求x的值,并说出此时四边形CHOK是什么特殊四边形.

查看答案和解析>>
科目:czsx
来源:
题型:解答题
13.

如图,在△ABC中,∠ACB=90°,AC=BC=6,现将一块边长足够大的直角三角板的直角顶点置于AB的中点O,两直角边分别经过点B、C,然后将三角板绕点O按顺时针方向旋转一个角度α(0°<α<90°),旋转后,直角三角板的直角边分别与AC、BC相交于点K、H,四边形CHOK是旋转过程中三角板与△ABC的重叠部分(如图所示),那么,在上述旋转过程中:
(1)线段BH与CK具有怎样的数量关系?四边形CHOK的面积是否发生变化?证明你发现的结论;
(2)连接HK,设BH=x.
①当△CKH的面积为$\frac{5}{2}$时,求出x的值.
②试问△OHK的面积是否存在最小值,若存在,求出此时x的值,若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:2013届河北省石家庄市第42中学九年级第一次模拟考试数学试卷(带解析)
题型:解答题
如图,在Rt△ABC中,∠ACB=90°,AC=6 cm ,BC=6cm,经过A,B的直线l以1cm/秒的速度向下作匀速平移运动,交BC于点B′,交CD于点 D′,与此同时,点P从点B′ 出发,在直线l上以1cm/秒的速度沿直线l向右下方向作匀速运动.设它们运动的时间为t秒.
cm ,BC=6cm,经过A,B的直线l以1cm/秒的速度向下作匀速平移运动,交BC于点B′,交CD于点 D′,与此同时,点P从点B′ 出发,在直线l上以1cm/秒的速度沿直线l向右下方向作匀速运动.设它们运动的时间为t秒.
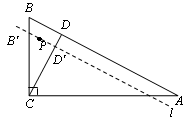
(1)你求出的AB的长是 ;
(2)过点C作CD⊥AB于点D,t为何值时,点P移动到CD上?
(3)t为何值时,以点P为圆心、1cm为半径的圆与直线CD相切?
(4)以点P为圆心、1 cm为半径的⊙P与CD所在的直线相交时,是否存在点P与两个交点构成的三角形是等边三角形?若存在,直接写出t的值;若不存在,说明理由.
查看答案和解析>>
科目:czsx
来源:2012-2013学年河北省石家庄市九年级第一次模拟考试数学试卷(解析版)
题型:解答题
如图,在Rt△ABC中,∠ACB=90°,AC=6 cm ,BC=6cm,经过A,B的直线l以1cm/秒的速度向下作匀速平移运动,交BC于点B′,交CD于点 D′,与此同时,点P从点B′ 出发,在直线l上以1cm/秒的速度沿直线l向右下方向作匀速运动.设它们运动的时间为t秒.
cm ,BC=6cm,经过A,B的直线l以1cm/秒的速度向下作匀速平移运动,交BC于点B′,交CD于点 D′,与此同时,点P从点B′ 出发,在直线l上以1cm/秒的速度沿直线l向右下方向作匀速运动.设它们运动的时间为t秒.

(1)你求出的AB的长是 ;
(2)过点C作CD⊥AB于点D,t为何值时,点P移动到CD上?
(3)t为何值时,以点P为圆心、1cm为半径的圆与直线CD相切?
(4)以点P为圆心、1 cm为半径的⊙P与CD所在的直线相交时,是否存在点P与两个交点构成的三角形是等边三角形?若存在,直接写出t的值;若不存在,说明理由.
查看答案和解析>>
科目:czsx
来源:不详
题型:解答题
如图,在Rt△ABC中,∠ACB=90°,AC=6

cm ,BC=6cm,经过A,B的直线l以1cm/秒的速度向下作匀速平移运动,交BC于点B′,交CD于点 D′,与此同时,点P从点B′ 出发,在直线l上以1cm/秒的速度沿直线l向右下方向作匀速运动.设它们运动的时间为t秒.

(1)你求出的AB的长是
;
(2)过点C作CD⊥AB于点D,t为何值时,点P移动到CD上?
(3)t为何值时,以点P为圆心、1cm为半径的圆与直线CD相切?
(4)以点P为圆心、1 cm为半径的⊙P与CD所在的直线相交时,是否存在点P与两个交点构成的三角形是等边三角形?若存在,直接写出t的值;若不存在,说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
19.已知:如图,在Rt△ABC中,∠ACB=90°,AC=15,BC=20,CD⊥AB,垂足为D,点E是点D关于AC的对称点,连接AE,CE.
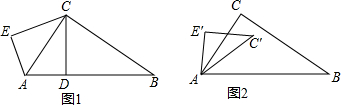
(1)求CD和AD的长;
(2)若将△ACE沿着射线AB方向平移,设平移的距离为m(平移距离指点A沿AB方向所经过的线段长度),当点E平移到线段AC上时,求m的值;
(3)如下图,将△ACE绕点A顺时针旋转-个角α(0°<α<180°),记旋转中的△ACE为△AC′E′,在旋转过程中,设C′E′所在的直线与直线BC交于点P,与直线AB交于点Q,若存在这样的P,Q两点,使△BPQ为等腰三角形,直接写出此时AQ的长,若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
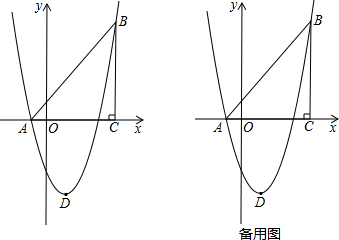
如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90,AC=BC,OA=1,
OC=4,抛物线 经过A,B两点,抛物线的顶点为D.
经过A,B两点,抛物线的顶点为D.
(1)求b,c的值;
(2)点E是直角三角形ABC斜边AB上一动点(点A、B除外),过点E作x轴的垂线
交抛物线于点F,当线段EF的长度最大时,求点E的坐标;
(3)在(2)的条件下:①求以点E、B、F、D为顶点的四边形的面积;②在抛物线上
是否存在一点P,使△EFP是以EF为直角边的直角三角形? 若存在,求出所有点P的
坐标;若不存在,说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
如图,在平面直角坐标系中,△AB C是直角三角形,∠ACB=90,AC=BC,OA=1,
C是直角三角形,∠ACB=90,AC=BC,OA=1,
OC=4,抛物线 经过A,B两点,抛物线的顶点为D.
经过A,B两点,抛物线的顶点为D.
(1)求b,c的值;
(2)点E是直角三角形ABC斜边AB上一 动点(点A、B除外)
动点(点A、B除外) ,过点E作x轴的垂线交抛物线于点F,当线段EF的长度最大时,求点E的坐标;
,过点E作x轴的垂线交抛物线于点F,当线段EF的长度最大时,求点E的坐标;
(3)在(2)的条件下:
①求以点E、B、F、D为顶点的四边形的面积;
②在抛物线上是否存在一点P,使△EFP是以EF为直角边的直角三角形? 若存在,求出所有点P的坐标;若不存在,说明 理由.
理由.

查看答案和解析>>
科目:czsx
来源:2016届江苏省九年级下学期第一次月考数学试卷(解析版)
题型:解答题
如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90,AC=BC,OA=1,OC=4,抛物线y= +bx+c经过A,B两点,抛物线的顶点为D.
+bx+c经过A,B两点,抛物线的顶点为D.

(1)、求b,c的值;
(2)、点E是直角三角形ABC斜边AB上一动点(点A、B除外),过点E作x轴的垂线交抛物线于点F,当线段EF的长度最大时,求点E的坐标;
(3)、在(2)的条件下:①求以点E、B、F、D为顶点的四边形的面积;②在抛物线上是否存在一点P,使△EFP是以EF为直角边的直角三角形? 若存在,求出所有点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90,AC=BC,OA=1,OC=4,抛物线y

=x
2+bx+c经过A,B两点,抛物线的顶点为D.
(1)求b,c的值;
(2)点E是直角三角形ABC斜边AB上一动点(点A、B除外),过点E作x轴的垂线交抛物线于点F,当线段EF的长度最大时,求点E的坐标;
(3)在(2)的条件下:
①求以点E、B、F、D为顶点的四边形的面积;
②在抛物线上是否存在一点P,使△EFP是以EF为直角边的直角三角形?若存在,求出所有点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90,AC=BC,OA=1,OC=4,抛物线y=x2+bx+c经过A,B两点,抛物线的顶点为D.
(1)b=______,c=______;
(2)点E是Rt△ABC斜边AB上一动点(点A、B除外),过点E作x轴的垂线交抛物线于点F,当线段EF的长度最大时,求点E的坐标;
(3)在(2)的条件下,抛物线上是否存在一点P,使△EFP是以EF为直角边的直角三角形?若存在,求出所有点P的坐标;若不存在,说明理由.
查看答案和解析>>

 在△ABC中,∠ACB=90°,AC=BC=4,现将一块边长足够大的直角三角板的直角顶点置于AB的中点O,两直角边分别经过点B、C,然后将三角板绕点O按顺时针方向旋转一个角度α(0°<α<90°),旋转后,直角三角板的直角边分别与AC、BC相交于点K、H,四边形CHOK是旋转过程中三角板与△ABC的重叠部分(如图所示),那么,在上述旋转过程中:
在△ABC中,∠ACB=90°,AC=BC=4,现将一块边长足够大的直角三角板的直角顶点置于AB的中点O,两直角边分别经过点B、C,然后将三角板绕点O按顺时针方向旋转一个角度α(0°<α<90°),旋转后,直角三角板的直角边分别与AC、BC相交于点K、H,四边形CHOK是旋转过程中三角板与△ABC的重叠部分(如图所示),那么,在上述旋转过程中: 在△ABC中,∠ACB=90°,AC=BC=4,现将一块边长足够大的直角三角板的直角顶点置于AB的中点O,两直角边分别经过点B、C,然后将三角板绕点O按顺时针方向旋转一个角度α(0°<α<90°),旋转后,直角三角板的直角边分别与AC、BC相交于点K、H,四边形CHOK是旋转过程中三角板与△ABC的重叠部分(如图所示),那么,在上述旋转过程中:
在△ABC中,∠ACB=90°,AC=BC=4,现将一块边长足够大的直角三角板的直角顶点置于AB的中点O,两直角边分别经过点B、C,然后将三角板绕点O按顺时针方向旋转一个角度α(0°<α<90°),旋转后,直角三角板的直角边分别与AC、BC相交于点K、H,四边形CHOK是旋转过程中三角板与△ABC的重叠部分(如图所示),那么,在上述旋转过程中: 时,求出x的值.
时,求出x的值. 已知在△ABC中,∠ACB=90°,AC=BC=4,现将一块边长足够大的直角三角板的直角顶点置于AB的中点O,两直角边分别经过点B、C,然后将三角板绕点O按顺时针方向旋转一个角度α(0°<α<90°),旋转后,直角三角板的直角边分别与AC、BC相交于点K、H,四边形CHOK是旋转过程中三角板与△ABC的重叠部分(如图所示).那么,在上述旋转过程中:
已知在△ABC中,∠ACB=90°,AC=BC=4,现将一块边长足够大的直角三角板的直角顶点置于AB的中点O,两直角边分别经过点B、C,然后将三角板绕点O按顺时针方向旋转一个角度α(0°<α<90°),旋转后,直角三角板的直角边分别与AC、BC相交于点K、H,四边形CHOK是旋转过程中三角板与△ABC的重叠部分(如图所示).那么,在上述旋转过程中: 已知在△ABC中,∠ACB=90°,AC=BC=4,现将一块边长足够大的直角三角板的直角顶点置于AB的中点O,两直角边分别经过点B、C,然后将三角板绕点O按顺时针方向旋转一个角度α(0°<α<90°),旋转后,直角三角板的直角边分别与AC、BC相交于点K、H,四边形CHOK是旋转过程中三角板与△ABC的重叠部分(如图所示).那么,在上述旋转过程中:
已知在△ABC中,∠ACB=90°,AC=BC=4,现将一块边长足够大的直角三角板的直角顶点置于AB的中点O,两直角边分别经过点B、C,然后将三角板绕点O按顺时针方向旋转一个角度α(0°<α<90°),旋转后,直角三角板的直角边分别与AC、BC相交于点K、H,四边形CHOK是旋转过程中三角板与△ABC的重叠部分(如图所示).那么,在上述旋转过程中: 时,求出x的值.
时,求出x的值. 时,求出x的值.
时,求出x的值.




 如图,在△ABC中,∠ACB=90°,AC=BC=6,现将一块边长足够大的直角三角板的直角顶点置于AB的中点O,两直角边分别经过点B、C,然后将三角板绕点O按顺时针方向旋转一个角度α(0°<α<90°),旋转后,直角三角板的直角边分别与AC、BC相交于点K、H,四边形CHOK是旋转过程中三角板与△ABC的重叠部分(如图所示),那么,在上述旋转过程中:
如图,在△ABC中,∠ACB=90°,AC=BC=6,现将一块边长足够大的直角三角板的直角顶点置于AB的中点O,两直角边分别经过点B、C,然后将三角板绕点O按顺时针方向旋转一个角度α(0°<α<90°),旋转后,直角三角板的直角边分别与AC、BC相交于点K、H,四边形CHOK是旋转过程中三角板与△ABC的重叠部分(如图所示),那么,在上述旋转过程中: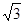 cm ,BC=6cm,经过A,B的直线l以1cm/秒的速度向下作匀速平移运动,交BC于点B′,交CD于点 D′,与此同时,点P从点B′ 出发,在直线l上以1cm/秒的速度沿直线l向右下方向作匀速运动.设它们运动的时间为t秒.
cm ,BC=6cm,经过A,B的直线l以1cm/秒的速度向下作匀速平移运动,交BC于点B′,交CD于点 D′,与此同时,点P从点B′ 出发,在直线l上以1cm/秒的速度沿直线l向右下方向作匀速运动.设它们运动的时间为t秒.
 cm ,BC=6cm,经过A,B的直线l以1cm/秒的速度向下作匀速平移运动,交BC于点B′,交CD于点 D′,与此同时,点P从点B′ 出发,在直线l上以1cm/秒的速度沿直线l向右下方向作匀速运动.设它们运动的时间为t秒.
cm ,BC=6cm,经过A,B的直线l以1cm/秒的速度向下作匀速平移运动,交BC于点B′,交CD于点 D′,与此同时,点P从点B′ 出发,在直线l上以1cm/秒的速度沿直线l向右下方向作匀速运动.设它们运动的时间为t秒.
 cm ,BC=6cm,经过A,B的直线l以1cm/秒的速度向下作匀速平移运动,交BC于点B′,交CD于点 D′,与此同时,点P从点B′ 出发,在直线l上以1cm/秒的速度沿直线l向右下方向作匀速运动.设它们运动的时间为t秒.
cm ,BC=6cm,经过A,B的直线l以1cm/秒的速度向下作匀速平移运动,交BC于点B′,交CD于点 D′,与此同时,点P从点B′ 出发,在直线l上以1cm/秒的速度沿直线l向右下方向作匀速运动.设它们运动的时间为t秒.

![]() 经过A,B两点,抛物线的顶点为D.
经过A,B两点,抛物线的顶点为D.
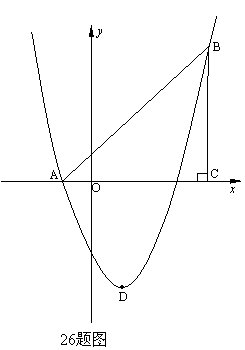
![]() C是直角三角形,∠ACB=90,AC=BC,OA=1,
C是直角三角形,∠ACB=90,AC=BC,OA=1,![]() 经过A,B两点,抛物线的顶点为D.
经过A,B两点,抛物线的顶点为D.![]() 动点(点A、B除外)
动点(点A、B除外)![]() ,过点E作x轴的垂线交抛物线于点F,当线段EF的长度最大时,求点E的坐标;
,过点E作x轴的垂线交抛物线于点F,当线段EF的长度最大时,求点E的坐标;![]() 理由.
理由.
 +bx+c经过A,B两点,抛物线的顶点为D.
+bx+c经过A,B两点,抛物线的顶点为D.
 =x2+bx+c经过A,B两点,抛物线的顶点为D.
=x2+bx+c经过A,B两点,抛物线的顶点为D.