如图.在rt三角形abc中.角c=90,ad是角bac答案解析
科目:czsx
来源:
题型:填空题
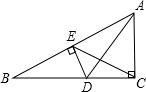 如图在Rt△ABC中,∠ACB=90°,∠B=30°,AD是∠BAC的平分线,DE⊥AB于点E,连接CE,则图中的等腰三角形共有________个.
如图在Rt△ABC中,∠ACB=90°,∠B=30°,AD是∠BAC的平分线,DE⊥AB于点E,连接CE,则图中的等腰三角形共有________个.
查看答案和解析>>
科目:czsx
来源:不详
题型:填空题
如图在Rt△ABC中,∠ACB=90°,∠B=30°,AD是∠BAC的平分线,DE⊥AB于点E,连接CE,则图中的等腰三角形共有______个.
查看答案和解析>>
科目:czsx
来源:第4章《视图与投影》易错题集(78):4.1 视图(解析版)
题型:填空题
如图在Rt△ABC中,∠ACB=90°,∠B=30°,AD是∠BAC的平分线,DE⊥AB于点E,连接CE,则图中的等腰三角形共有
个.

查看答案和解析>>
科目:czsx
来源:第1章《证明(二)》易错题集(11):1.2 直角三角形(解析版)
题型:填空题
如图在Rt△ABC中,∠ACB=90°,∠B=30°,AD是∠BAC的平分线,DE⊥AB于点E,连接CE,则图中的等腰三角形共有
个.

查看答案和解析>>
科目:czsx
来源:第1章《证明(二)》易错题集(05):1.1 你能证明它们吗(解析版)
题型:填空题
如图在Rt△ABC中,∠ACB=90°,∠B=30°,AD是∠BAC的平分线,DE⊥AB于点E,连接CE,则图中的等腰三角形共有
个.

查看答案和解析>>
科目:czsx
来源:
题型:

20、如图在Rt△ABC中,∠ACB=90°,∠B=30°,AD是∠BAC的平分线,DE⊥AB于点E,连接CE,则图中的等腰三角形共有
4
个.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
请阅读下列材料:
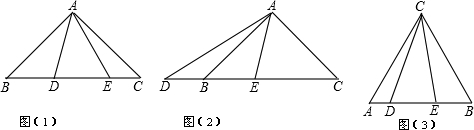
已知:如图(1)在Rt△ABC中,∠BAC=90°,AB=AC,点D、E分别为线段BC上两动点,若∠DAE=45°.探究线段BD、DE、EC三条线段之间的数量关系.小明的思路是:把△AEC绕点A顺时针旋转90°,得到△ABE′,连接E′D,使问题得到解决.请你参考小明的思路探究并解决下列问题:
(1)猜想BD、DE、EC三条线段之间存在的数量关系式,直接写出你的猜想;
(2)当动点E在线段BC上,动点D运动在线段CB延长线上时,如图(2),其它条件不变,(1)中探究的结论是否发生改变?请说明你的猜想并给予证明;
(3)已知:如图(3),等边三角形ABC中,点D、E在边AB上,且∠DCE=30°,请你找出一个条件,使线段DE、AD、EB能构成一个等腰三角形,并求出此时等腰三角形顶角的度数.
查看答案和解析>>
科目:czsx
来源:2010年中考复习针对性训练 几何探究题(解析版)
题型:解答题
请阅读下列材料:
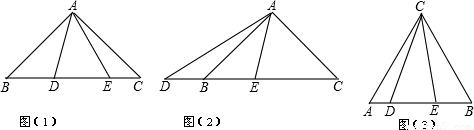
已知:如图(1)在Rt△ABC中,∠BAC=90°,AB=AC,点D、E分别为线段BC上两动点,若∠DAE=45°.探究线段BD、DE、EC三条线段之间的数量关系.小明的思路是:把△AEC绕点A顺时针旋转90°,得到△ABE′,连接E′D,使问题得到解决.请你参考小明的思路探究并解决下列问题:
(1)猜想BD、DE、EC三条线段之间存在的数量关系式,直接写出你的猜想;
(2)当动点E在线段BC上,动点D运动在线段CB延长线上时,如图(2),其它条件不变,(1)中探究的结论是否发生改变?请说明你的猜想并给予证明;
(3)已知:如图(3),等边三角形ABC中,点D、E在边AB上,且∠DCE=30°,请你找出一个条件,使线段DE、AD、EB能构成一个等腰三角形,并求出此时等腰三角形顶角的度数.
查看答案和解析>>
科目:czsx
来源:
题型:阅读理解
11、请阅读下列材料:
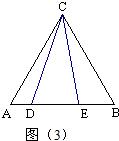
已知:如图(1)在Rt△ABC中,∠BAC=90°,AB=AC,点D、E分别为线段BC上两动点,若∠DAE=45°.探究线段BD、DE、EC三条线段之间的数量关系.小明的思路是:把△AEC绕点A顺时针旋转90°,得到△ABE′,连接E′D,使问题得到解决.请你参考小明的思路探究并解决下列问题:
(1)猜想BD、DE、EC三条线段之间存在的数量关系式,直接写出你的猜想;
(2)当动点E在线段BC上,动点D运动在线段CB延长线上时,如图(2),其它条件不变,(1)中探究的结论是否发生改变?请说明你的猜想并给予证明;
(3)已知:如图(3),等边三角形ABC中,点D、E在边AB上,且∠DCE=30°,请你找出一个条件,使线段DE、AD、EB能构成一个等腰三角形,并求出此时等腰三角形顶角的度数.

查看答案和解析>>
科目:czsx
来源:
题型:
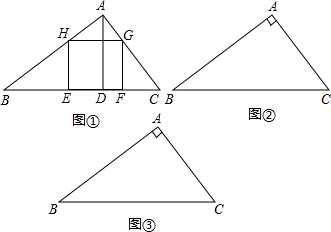
如果正方形的一边落在三角形的一边上,其余两个顶点分别在三角形的另外两条边上,则这样的正方形叫做三角形的内接正方形.
(1)如图①,在△ABC中,BC=a,BC边上的高AD=h
a,EFGH是△ABC的内接正方形.设正方形EFGH的边长是x,求证:
x=;
(2)在Rt△ABC中,AB=4,AC=3,∠BAC=90度.请在图②,图③中分别画出可能的内接正方形,并根据计算回答哪个内接正方形的面积最大;
(3)在锐角△ABC中,BC=a,AC=b,AB=c,且a<b<c.请问这个三角形的内接正方形中哪个面积最大?并说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
如果正方形的一边落在三角形的一边上,其余两个顶点分别在三角形的另外两条边上,则这样的正方形叫做三角形的内接正方形.
(1)如图①,在△ABC中,BC=a,BC边上的高AD=ha,EFGH是△ABC的内接正方形.设正方形EFGH的边长是x,求证: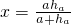 ;
;
(2)在Rt△ABC中,AB=4,AC=3,∠BAC=90度.请在图②,图③中分别画出可能的内接正方形,并根据计算回答哪个内接正方形的面积最大;
(3)在锐角△ABC中,BC=a,AC=b,AB=c,且a<b<c.请问这个三角形的内接正方形中哪个面积最大?并说明理由.

查看答案和解析>>
科目:czsx
来源:不详
题型:解答题
如果正方形的一边落在三角形的一边上,其余两个顶点分别在三角形的另外两条边上,则这样的正方形叫做三角形的内接正方形.
(1)如图①,在△ABC中,BC=a,BC边上的高AD=h
a,EFGH是△ABC的内接正方形.设正方形EFGH的边长是x,求证:
x=;
(2)在Rt△ABC中,AB=4,AC=3,∠BAC=90度.请在图②,图③中分别画出可能的内接正方形,并根据计算回答哪个内接正方形的面积最大;
(3)在锐角△ABC中,BC=a,AC=b,AB=c,且a<b<c.请问这个三角形的内接正方形中哪个面积最大?并说明理由.

查看答案和解析>>
科目:czsx
来源:
题型:

已知:如图,在Rt△ABC中,∠ABC=90°,AB=4,
sin∠BAC=,P是边AC上一点,过点P作PD⊥AC,过点A作AD∥BC,交PD于点D,连接并延长DC,交边AB的延长线于点E.设A、P两点的距离为x,B、E两点的距离为y.
(1)求BC的长度;
(2)求y关于x的函数解析式,并写出它的定义域;
(3)当△ACD是等腰三角形时,求BE的长.
查看答案和解析>>
科目:czsx
来源:2004年全国中考数学试题汇编《图形的相似》(03)(解析版)
题型:解答题
(2004•佛山)如果正方形的一边落在三角形的一边上,其余两个顶点分别在三角形的另外两条边上,则这样的正方形叫做三角形的内接正方形.
(1)如图①,在△ABC中,BC=a,BC边上的高AD=h
a,EFGH是△ABC的内接正方形.设正方形EFGH的边长是x,求证:
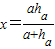
;
(2)在Rt△ABC中,AB=4,AC=3,∠BAC=90度.请在图②,图③中分别画出可能的内接正方形,并根据计算回答哪个内接正方形的面积最大;
(3)在锐角△ABC中,BC=a,AC=b,AB=c,且a<b<c.请问这个三角形的内接正方形中哪个面积最大?并说明理由.

查看答案和解析>>
科目:czsx
来源:2004年全国中考数学试题汇编《四边形》(06)(解析版)
题型:解答题
(2004•佛山)如果正方形的一边落在三角形的一边上,其余两个顶点分别在三角形的另外两条边上,则这样的正方形叫做三角形的内接正方形.
(1)如图①,在△ABC中,BC=a,BC边上的高AD=h
a,EFGH是△ABC的内接正方形.设正方形EFGH的边长是x,求证:

;
(2)在Rt△ABC中,AB=4,AC=3,∠BAC=90度.请在图②,图③中分别画出可能的内接正方形,并根据计算回答哪个内接正方形的面积最大;
(3)在锐角△ABC中,BC=a,AC=b,AB=c,且a<b<c.请问这个三角形的内接正方形中哪个面积最大?并说明理由.

查看答案和解析>>
科目:czsx
来源:2004年广东省佛山市中考数学试卷(解析版)
题型:解答题
(2004•佛山)如果正方形的一边落在三角形的一边上,其余两个顶点分别在三角形的另外两条边上,则这样的正方形叫做三角形的内接正方形.
(1)如图①,在△ABC中,BC=a,BC边上的高AD=h
a,EFGH是△ABC的内接正方形.设正方形EFGH的边长是x,求证:

;
(2)在Rt△ABC中,AB=4,AC=3,∠BAC=90度.请在图②,图③中分别画出可能的内接正方形,并根据计算回答哪个内接正方形的面积最大;
(3)在锐角△ABC中,BC=a,AC=b,AB=c,且a<b<c.请问这个三角形的内接正方形中哪个面积最大?并说明理由.

查看答案和解析>>
科目:czsx
来源:
题型:

多彩数学,所有三角形都是等腰三角形
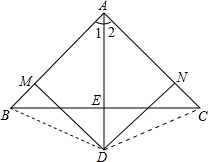
下面的推理过程,请你指出其错误之处.如图:△ABC中,∠BAC的平分线和BC边的垂直平分线相交于D,过点D作DM⊥AB于M,DN⊥AC于N.求证:AB=AC.
证明:连结BD、CD.
∵DM⊥AB,∴∠DMA=90°.∵DN⊥AC,∴∠AND=90°.∴∠AMD=∠AND=90°.又AD平分∠BAC,∴∠1=∠2.又∵AD=AD,∵△ADM≌△ADN(AAS),∴AM=AN,DM=DN.∵DE垂直平分BC,∴DB=DC.在Rt△BDM与Rt△CDN中,
∴Rt△BDM≌Rt△CDN(HL),∴BM=CN.又∵AM=AN,∴AB=AC,∴△ABC一定是等腰三角形.你认为对吗?
分三种情况:
(1)AB=AC时成立;
(2)AB>AC时,N在AC的延长线上;
(3)AB<AC时,M在AB的延长线上.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
 多彩数学,所有三角形都是等腰三角形
多彩数学,所有三角形都是等腰三角形
下面的推理过程,请你指出其错误之处.如图:△ABC中,∠BAC的平分线和BC边的垂直平分线相交于D,过点D作DM⊥AB于M,DN⊥AC于N.求证:AB=AC.
证明:连结BD、CD.
∵DM⊥AB,∴∠DMA=90°.∵DN⊥AC,∴∠AND=90°.∴∠AMD=∠AND=90°.又AD平分∠BAC,∴∠1=∠2.又∵AD=AD,∵△ADM≌△ADN(AAS),∴AM=AN,DM=DN.∵DE垂直平分BC,∴DB=DC.在Rt△BDM与Rt△CDN中,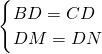 ∴Rt△BDM≌Rt△CDN(HL),∴BM=CN.又∵AM=AN,∴AB=AC,∴△ABC一定是等腰三角形.你认为对吗?
∴Rt△BDM≌Rt△CDN(HL),∴BM=CN.又∵AM=AN,∴AB=AC,∴△ABC一定是等腰三角形.你认为对吗?
分三种情况:
(1)AB=AC时成立;
(2)AB>AC时,N在AC的延长线上;
(3)AB<AC时,M在AB的延长线上.
查看答案和解析>>
科目:czsx
来源:
题型:填空题
【阅读理解】
已知:如图1,等腰直角三角形ABC中,∠B=90°,AD是角平分线,交BC边于点D.求证:AC=AB+BD证明:如图1,在AC上截取AE=AB,连接DE,则由已知条件易知:Rt△ADB≌Rt△ADE(AAS)
∴∠AED=∠B=90°,DE=DB
又∵∠C=45°,∴△DEC是等腰直角三角形.
∴DE=EC.
∴AC=AE+EC=AB+BD.
【解决问题】
已知,如图2,等腰直角三角形ABC中,∠B=90°,AD是∠BAC的平分线,交BC边于点D,DE⊥AC,垂足为E,若AB=2,则三角形DEC的周长为________.
【数学思考】:现将原题中的“AD是内角平分线,交BC边于点D”换成“AD是外角平分线,交BC边的延长线于点D如图3”,其他条件不变,请你猜想线段AC、AB、BD之间的数量关系,并证明你的猜想.
【类比猜想】
任意三角形ABC,∠ABC=2∠C,AD是∠BAC的外角平分线,交CB边的延长线于点D,如图4,请你写出线段AC、AB、BD之间的数量关系.
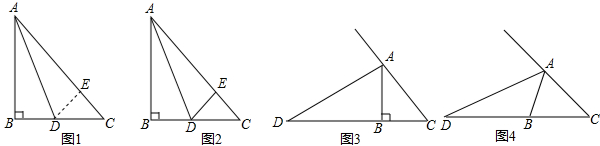
查看答案和解析>>
科目:czsx
来源:
题型:
【阅读理解】
已知:如图1,等腰直角三角形ABC中,∠B=90°,AD是角平分线,交BC边于点D.求证:AC=AB+BD证明:如图1,在AC上截取AE=AB,连接DE,则由已知条件易知:Rt△ADB≌Rt△ADE(AAS)
∴∠AED=∠B=90°,DE=DB
又∵∠C=45°,∴△DEC是等腰直角三角形.
∴DE=EC.
∴AC=AE+EC=AB+BD.
【解决问题】
已知,如图2,等腰直角三角形ABC中,∠B=90°,AD是∠BAC的平分线,交BC边于点D,DE⊥AC,垂足为E,若AB=2,则三角形DEC的周长为
.
【数学思考】:现将原题中的“AD是内角平分线,交BC边于点D”换成“AD是外角平分线,交BC边的延长线于点D如图3”,其他条件不变,请你猜想线段AC、AB、BD之间的数量关系,并证明你的猜想.
【类比猜想】
任意三角形ABC,∠ABC=2∠C,AD是∠BAC的外角平分线,交CB边的延长线于点D,如图4,请你写出线段AC、AB、BD之间的数量关系.
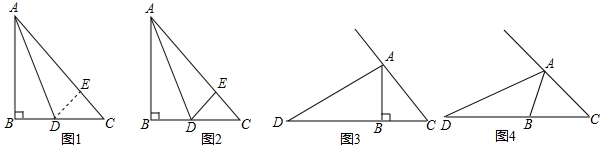
查看答案和解析>>

 如图在Rt△ABC中,∠ACB=90°,∠B=30°,AD是∠BAC的平分线,DE⊥AB于点E,连接CE,则图中的等腰三角形共有________个.
如图在Rt△ABC中,∠ACB=90°,∠B=30°,AD是∠BAC的平分线,DE⊥AB于点E,连接CE,则图中的等腰三角形共有________个.








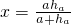 ;
;

 已知:如图,在Rt△ABC中,∠ABC=90°,AB=4,sin∠BAC=
已知:如图,在Rt△ABC中,∠ABC=90°,AB=4,sin∠BAC=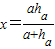 ;
;
 ;
;
 ;
;
 多彩数学,所有三角形都是等腰三角形
多彩数学,所有三角形都是等腰三角形 多彩数学,所有三角形都是等腰三角形
多彩数学,所有三角形都是等腰三角形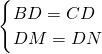 ∴Rt△BDM≌Rt△CDN(HL),∴BM=CN.又∵AM=AN,∴AB=AC,∴△ABC一定是等腰三角形.你认为对吗?
∴Rt△BDM≌Rt△CDN(HL),∴BM=CN.又∵AM=AN,∴AB=AC,∴△ABC一定是等腰三角形.你认为对吗?
