如下图.已知AD⊥BC, EF⊥BC, ∠1=∠C.证明:∠2=∠3答案解析
科目:czsx
来源:同步题
题型:解答题
如下图,已知AD⊥BC,EF⊥BC,∠1=∠2,求证:DG∥BA
证明:∵AD⊥BC,EF⊥BC ( )
∴∠EFB=∠ADB=90°( )
∴EF∥AD( )
∴∠1=∠BAD( )
又∵∠1=∠2 ( )
∴_________( )
∴DG∥BA( )。
查看答案和解析>>
科目:czsx
来源:广东省期末题
题型:解答题
填空:把下面的推理过程补充完整,并在括号内注明理由。
如下图,点B、D在线段AE上,BC∥EF,AD=BE,BC=EF。
求证:(1)∠C=∠F;
(2)AC∥DF。
证明:(1)∵BC∥EF(已知)
∴∠ABC=( )( )
∵AD=BE
∴AD+DB=DB+BE
即( ) =DE
在△ABC与△DEF中
∠ABC=∠EBC=EF( )
∴△ABC≌△DEF( )
∴∠C=∠F( );
(2)∵△ABC≌△DEF
∴∠A=∠FDE( )
∴AC∥DF( )。
查看答案和解析>>
科目:czsx
来源:
题型:
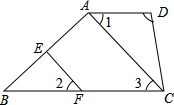
已知:如图①,△ABC为边长为2的等边三角形,D、E、F分别为AB、AC、BC中点,连接DE、DF、EF.将△BDF向右平移,使点B与点C重合;将△ADE向下平移,使点A与点C重合,如图②.
(1)设△ADE、△BDF、△EFC的面积分别为 S
1、S
2、S
3,则S
1+S
2+S
3 (用“<、=、>”填空)
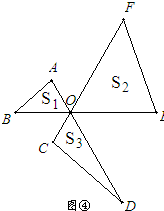
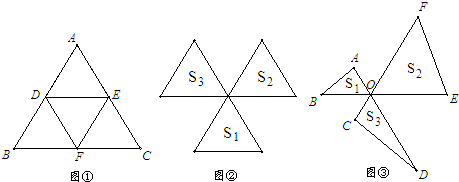
(2)已知:如图③,∠AOB=∠COD=∠EOF=60°,AD=CF=BE=2,设△ABO、△FEO、△CDO的面积分别为S
1、S
2、S
3;问:上述结论是否成立?若成立,请给出证明;若不成立,请说明理由.(可利用图④进行探究)
查看答案和解析>>
科目:czsx
来源:
题型:
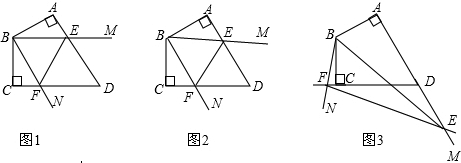
已知四边形ABCD中,AB=BC,∠ABC=120°,∠MBN=60°,∠MBN绕B点旋转,它的两边分别交AD,DC(或它们的延长线)于E,F.
当∠MBN绕B点旋转到AE=CF时(如图1),易证AE+CF=EF;
当∠MBN绕B点旋转到AE≠CF时,在图2和图3这两种情况下,上述结论是否成立?若成立,请给予证明;若不成立,线段AE,CF,EF又有怎样的数量关系?请写出你的猜想,不需证明.
查看答案和解析>>
科目:czsx
来源:
题型:
如图,已知矩形
ABCD,AB=,BC=3,在BC上取两点E,F(E在F左边),以EF为边作等边
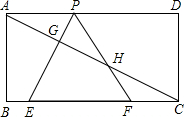
三角形PEF,使顶点P在AD上,PE,PF分别交AC于点G,H.
(1)求△PEF的边长;
(2)在不添加辅助线的情况下,当F与C不重合时,先直接判断△APH与△CFH是如下关系中的哪一种:然后证明你的判断.
①△APH与△CFH全等;
②△APH与△CFH相似;
③△APH与△CFH成中心对称;
④△APH与△CFH成轴对称;
(3)若△PEF的边EF在线段BC上移动.试猜想:PH与BE有何数量关系?并证明你猜想的结论.
查看答案和解析>>
科目:czsx
来源:
题型:
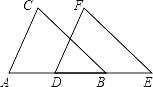
已知MN∥EF∥BC,点A、D为直线MN上的两动点,AD=a,BC=b.
(1)当点A、D重合,即a=0时(如图1),试求EF.(用含m,n,b的代数式表示)
(2)请直接应用(1)的结论解决下面问题:当A、D不重合,即a≠0,
①如图2这种情况时,试求EF.(用含a,b,m,n的代数式表示)
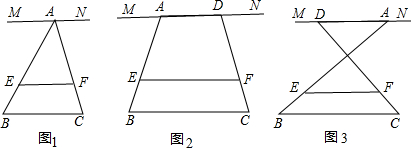
②如图3这种情况时,试猜想EF与a、b之间有何种数量关系?并证明你的猜想.
查看答案和解析>>
科目:czsx
来源:
题型:
如图,已知矩形ABCD,AB=
,BC=3,在BC上取两点E、F(E在F左边),以EF为边作等边三角
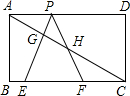
形PEF,使顶点P在AD上,PE、PF分别交AC于点G、H.
(1)求△PEF的边长;
(2)在不添加辅助线的情况下,从图中找出一个除△PEF外的等腰三角形,并说明理由;
(3)若△PEF的边EF在线段BC上移动.试猜想:PH与BE有何数量关系?并证明你猜想的结论.
查看答案和解析>>
科目:czsx
来源:
题型:
如图,已知矩形ABCD,AB=
,BC=3,在BC上取两点E,F(E在F左边),以EF为边作等边三
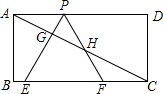
角形PEF,使顶点P在AD上,PE,PF分别交AC于点G,H.
(1)求△PEF的边长;
(2)在不添加辅助线的情况下,当F与C不重合时,从图中找出一对相似三角形,并说明理由;
(3)若△PEF的边EF在线段BC上移动.试猜想:PH与BE有何数量关系并证明你猜想的结论.
查看答案和解析>>
科目:czsx
来源:
题型:
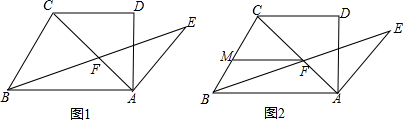
如图,已知直角梯形ABCD中,AB∥CD,∠D=90°,AB=AC,AE⊥AC且AE=AD,连BE交AC于F.
(1)如图1,若CD=AD,试猜想BF与EF的数量关系;
(2)如图2,若CD≠AD,问题(1)BF与EF的数量关系是否仍然成立?若成立,请证明.若不成立,请说明理由;
(3)如图2,在第(2)问的条件下,取BC中点M,问线段MF与线段BD之间是否存在某种确定的数量关系?若存在,证明你的结论,若不存在,说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
已知:正方形ABCD中,点F为边CD的中点,DF=3,连接AF并延长,与BC的延长线交于G点.
(1)连接BF(如图1),在不添加任何辅助线的条件下,请找出所有相似的三角形,并选择其中的一对加以证明;
(2)E是边CB上一动点,连接EF,M为AD上任意一点,且MF⊥EF,连接ME(如图2).若△MEF与△ADF相似,求EB的长.
查看答案和解析>>
科目:czsx
来源:
题型:
已知四边形ABCD中,AB⊥AD,BC⊥CD,AB=BC,∠ABC=120°,∠MBN=60°,∠MBN绕B点旋转,它的两边分别交AD,DC(或它们的延长线)于E、F,
(1)当∠MBN绕B点旋转到AE=CF时(如图1),试猜想AE,CF,EF之间存在怎样的数量关系?请将三条线段分别填入后面横线中:
AE
AE
+
CF
CF
=
EF
EF
(不需证明)
(2)当∠MBN绕B点旋转到AE≠CF时,在图2和图3这两种情况下,上问的结论分别是否仍然成立?若成立,请给出证明;若不成立,那么这三条线段又有怎样的数量关系?请写出你的猜想,不需证明.

查看答案和解析>>
科目:czsx
来源:
题型:
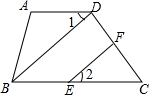
已知:如图,在四边形中ABCD,AD∥BC,E、F分别在边AB、BC上,且∠1=∠2.请你将下面证明过程补充完整,并在相应的括号内注明理由.
证明:∵AD∥BC,
∴∠1=
∠3
∠3
(
两直线平行,内错角相等
两直线平行,内错角相等
).
又∵∠1=
∠2
∠2
∴∠2=
∠3
∠3
(
等量代换
等量代换
).
∴EF∥AC(
同位角相等,两直线平行
同位角相等,两直线平行
)
查看答案和解析>>
科目:czsx
来源:
题型:
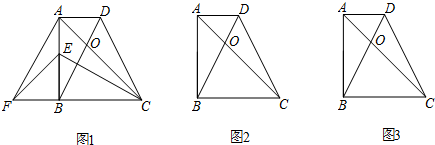
如图,在四边形ABCD中,∠A=134°-∠2,∠ABC=46°+∠2,BD⊥CD于点D,EF⊥CD于点F.求证:∠1=∠2.请你完成下面证明过程.
证明:∵∠A=134°-∠2,
∠ABC=46°+∠2,
已知
已知
∴∠A+∠ABC=134°-∠2+46°+∠2=180°.
(等式性质)
∴AD∥BC,
(同旁内角互补,两直线平行)
(同旁内角互补,两直线平行)
∴∠1=∠DBC,
(两直线平行,内错角相等)
(两直线平行,内错角相等)
∵BD⊥DC,EF⊥DC,
(已知)
(已知)
∴∠BDC=90°,∠EFC=90°,
(垂直定义)
(垂直定义)
∴∠BDC=∠EFC.
∴BD∥
EF
EF
.
(同位角相等,两直线平行)
(同位角相等,两直线平行)
∴∠2=∠DBC,
(两直线平行,同位角相等)
(两直线平行,同位角相等)
∴∠1=∠2.
(等量代换)
(等量代换)
.
查看答案和解析>>
科目:czsx
来源:
题型:
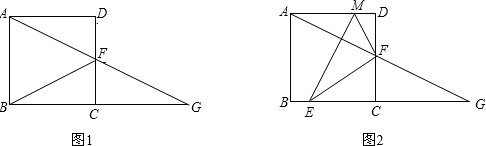
如图1,梯形ABCD中,AD∥BC,∠ABC=90°,且AD=1,AB=BC=2,对角线AC和BD相交于点O.点E在AB上,点F在CB延长线上,连结EF,且BE=BF.
(1)连结AF,CE,则线段AF与CE的位置关系是
,数量关系是
;
(2)将图1中的△EBF绕点B逆时针方向旋转旋转α角(0°<α<90°),连结AF、CE.试在图2中画出旋转后的图形,并判断此时(1)中的两个结论是否成立,写出你的猜想并加以证明;
(3)将图1中的△EBF绕点B逆时针旋转,使到一边BF落在线段BO上,此时△EBF的一边EF与BC交于点M,连结AF、CE.试在图3中画出旋转后的图形,并解答下列问题:
①此时(1)中的两个结论是否成立?(直接写出你的猜想,不必证明.)
②已知OF=
,试求BM的长.
查看答案和解析>>
科目:czsx
来源:1+1轻巧夺冠 同步讲解 九年级数学(下) 华东师大版
题型:059
|
|
如图,已知△ABC中,AD为BC边上中线,E为AC上一点,BE与AD交于F,若AE=EF
求证:AC=BF

证明:如图,延长FD交N,使DN=DF,连结CN.
在△BDF和△CDN中
∴△________≌△________.
∴∠3=∠N,BF=CN
∵AE=FE,∴∠________=∠________
∴∠3=∠2∴∠1=∠N
∴________=________∴BF=AC
阅读后回答下列问题:
| (1) |
|
(2) |
|
上述证明过程还有别的辅助线作法吗?若有,试选出一种________;
|
|
(3) |
|
若把AE=EF换成AD平行于∠BFC的平分线EG,其他条件不变,问原结论是否成立?请给予证明.
|
|
|
查看答案和解析>>
科目:czsx
来源:2006年福建省漳州市初中毕业暨高中阶段招生考试数学试题(实验区)
题型:059
如图,已知矩形ABCD,AB=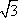 ,BC=3,在BC上取两点E,F(E在F左边),以EF为边作等边三角形PEF,使顶点P在AD上,PE,PF分别交AC于点G,H.
,BC=3,在BC上取两点E,F(E在F左边),以EF为边作等边三角形PEF,使顶点P在AD上,PE,PF分别交AC于点G,H.
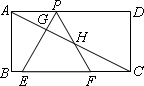
(1)求△PEF的边长;
(2)在不添加辅助线的情况下,当F与C不重合时,从图中找出一对相似三角形,并说明理由;
(3)若△PEF的边EF在线段BC上移动.试猜想:PH与BE有何数量关系?并证明你猜想的结论.
查看答案和解析>>
科目:czsx
来源:浙江省杭州市启正中学2011届九年级5月月考数学试题
题型:059
如图,已知矩形ABCD,AB=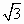 ,BC=3,在BC上取两点E、F(E在F左边),以EF为边作等边三角形PEF,使顶点P在AD上,PE、PF分别交AC于点G、H.
,BC=3,在BC上取两点E、F(E在F左边),以EF为边作等边三角形PEF,使顶点P在AD上,PE、PF分别交AC于点G、H.

(1)求△PEF的边长;
(2)在不添加辅助线的情况下,从图中找出一个除△PEF外的等腰三角形,并说明理由;
(3)若△PEF的边EF在线段BC上移动.试猜想:PH与BE有何数量关系?并证明你猜想的结论.
查看答案和解析>>
科目:czsx
来源:
题型:
如图,在下列矩形ABCD中,已知:AB=a,BC=b(a<b),假定顶点在矩形边上的菱形叫做矩形的内接菱形,现给出(Ⅰ)、(Ⅱ)、(Ⅲ)三个命题:
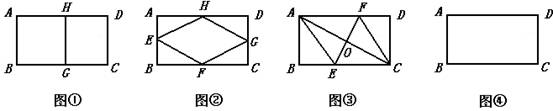
命题(Ⅰ):图①中,若AH=BG=AB,则四边形ABGH是矩形ABCD的内接菱形;
命题(Ⅱ):图②中,若点E、F、G和H分别是AB、BC、CD和DE的中点,则四边形EFGH是矩形ABCD的内接菱形;
命题(Ⅲ):图③中,若EF垂直平分对角线AC,变BC于点E,交AD于点F,交AC于点O,则四边形AECF是矩形ABCD的内接菱形.
请解决下列问题:
1.命题(Ⅰ)、(Ⅱ)、(Ⅲ)都是真命题吗?请你在其中选择一个,并证明它是真命题或假命题;
2.画出一个新的矩形内接菱形(即与你在(1)中所确认的,但不全等的内接菱形).
3.试探究比较图①,②,③中的四边形ABGH、EFGH、AECF的面积大小关系
查看答案和解析>>
科目:czsx
来源:
题型:
如图,已知矩形ABCD,AB=,BC=3,在BC上取两点E、F(E在F左边),以EF为边作等边三角形PEF,使顶点P在AD上,PE、PF分别交AC于点G、H.
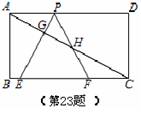
1.求△PEF的边长;
2.在不添加辅助线的情况下,从图中找出一个除△PEF外的等腰三角形,并说明理由
3.若△PEF的边EF在线段BC上移动.试猜想:PH与BE有何数量关系?并证明你猜想的结论.
查看答案和解析>>
科目:czsx
来源:
题型:
如图,已知矩形ABCD,AB=,BC=3,在BC上取两点E、F(E在F左边),以EF为边作等边三角形PEF,使顶点P在AD上,PE、PF分别交AC于点G、H.

【小题1】求△PEF的边长;
【小题2】在不添加辅助线的情况下,从图中找出一个除△PEF外的等腰三角形,并说明理由
【小题3】若△PEF的边EF在线段BC上移动.试猜想:PH与BE有何数量关系?并证明你猜想的结论.
查看答案和解析>>





 三角形PEF,使顶点P在AD上,PE,PF分别交AC于点G,H.
三角形PEF,使顶点P在AD上,PE,PF分别交AC于点G,H.
 形PEF,使顶点P在AD上,PE、PF分别交AC于点G、H.
形PEF,使顶点P在AD上,PE、PF分别交AC于点G、H. 角形PEF,使顶点P在AD上,PE,PF分别交AC于点G,H.
角形PEF,使顶点P在AD上,PE,PF分别交AC于点G,H.


 已知:如图,在四边形中ABCD,AD∥BC,E、F分别在边AB、BC上,且∠1=∠2.请你将下面证明过程补充完整,并在相应的括号内注明理由.
已知:如图,在四边形中ABCD,AD∥BC,E、F分别在边AB、BC上,且∠1=∠2.请你将下面证明过程补充完整,并在相应的括号内注明理由. 如图,在四边形ABCD中,∠A=134°-∠2,∠ABC=46°+∠2,BD⊥CD于点D,EF⊥CD于点F.求证:∠1=∠2.请你完成下面证明过程.
如图,在四边形ABCD中,∠A=134°-∠2,∠ABC=46°+∠2,BD⊥CD于点D,EF⊥CD于点F.求证:∠1=∠2.请你完成下面证明过程.
![]() ,BC=3,在BC上取两点E,F(E在F左边),以EF为边作等边三角形PEF,使顶点P在AD上,PE,PF分别交AC于点G,H.
,BC=3,在BC上取两点E,F(E在F左边),以EF为边作等边三角形PEF,使顶点P在AD上,PE,PF分别交AC于点G,H.
![]() ,BC=3,在BC上取两点E、F(E在F左边),以EF为边作等边三角形PEF,使顶点P在AD上,PE、PF分别交AC于点G、H.
,BC=3,在BC上取两点E、F(E在F左边),以EF为边作等边三角形PEF,使顶点P在AD上,PE、PF分别交AC于点G、H.


