如图矩形abcd对角线相交于点o.be平行ac求证菱形答案解析

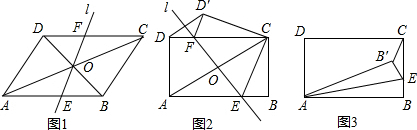
7．（1）如图1，在平行四边形ABCD中，对角线AC、BD相交于O点，过点O的直线l与边AB、CD分别交于点E、F，绕点O旋转直线l，猜想直线l旋转到什么位置时，四边形AECF是菱形．证明你的猜想．
（2）若将（1）中四边形ABCD改成矩形ABCD，使AB=4cm，BC=3cm，
①如图2，绕点O旋转直线l与边AB、CD分别交于点E、F，将矩形ABCD沿EF折叠，使点A与点C重合，点D的对应点为D′，连接DD′，求△DFD′的面积．
②如图3，绕点O继续旋转直线l，直线l与边BC或BC的延长线交于点E，连接AE，将矩形ABCD沿AE折叠，点B的对应点为B′，当△CEB′为直角三角形时，求BE的长度．请直接写出结果，不必写解答过程．

20．（1）如图1，在矩形ABCD中，对角线AC与BD相交于点O，过点O作直线EF⊥BD，且交AD于点E，交BC于点F，连接BE，DF，且BE平分∠ABD．
①求证：四边形BFDE是菱形；
②直接写出∠EBF的度数．
（2）把（1）中菱形BFDE进行分离研究，如图2，G，I分别在BF，BE边上，且BG=BI，连接GD，H为GD的中点，连接FH，并延长FH交ED于点J，连接IJ，IH，IF，IG．试探究线段IH与FH之间满足的关系，并说明理由；
（3）把（1）中矩形ABCD进行特殊化探究，如图3，矩形ABCD满足AB=AD时，点E是对角线AC上一点，连接DE，作EF⊥DE，垂足为点E，交AB于点F，连接DF，交AC于点G．请直接写出线段AG，GE，EC三者之间满足的数量关系．

19．我们给出如下定义：若一个四边形有一组对角互补（即对角之和为180°），则称这个四边形为圆满四边形．
（1）概念理解：在平行四边形、菱形、矩形、正方形中，你认为属于圆满四边形的有矩形，正方形．
（2）问题探究：如图，在四边形ABCD中，对角线AC、BD相交于点O，若∠ADB=∠ACB，问四边形ABCD是圆满四边形吗？请说明理由．小明经过思考后，判断四边形ABCD是圆满四边形，并提出了如下探究思路：先证明△AOD∽△BOC，得到比例式$\frac{OA}{OB}$=$\frac{OD}{OC}$，再证明△AOB∽△DOC，得出对应角相等，根据四边形内角和定理，得出一组对角互补．请你帮助小明写出解题过程．
（3）问题解决：请结合上述解题中所积累的经验和知识完成下题．如图‚，四边形ABCD中，AD⊥BD，AC⊥BC，AB与DC的延长线相交于点E，BE=BD，AB=5，AD=3，求CE的长．