
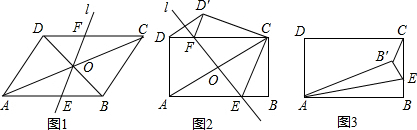
���� ��1������AF��CE������������ȫ��֤����OE=OF�����AC��EF����֤���ı���AECF�����Σ�
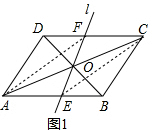
��2���ٹ�D����D��H��CF��H����DF=xcm����CF=��4-x��cm�������۵������ʵõ�D��F=DF=x��CD��=AD=3����CD��F=��ADC=90�㣬�ɹ��ɶ������x��ֵ�����ݵ����֪ʶ���D��H�ij������������DFD��������
�ڷ�������E���λ�ã�����ͼ�κ����ù��ɶ������۵������ʼ�������𰸣�
���  �⣺��1�����룺��l��ACʱ���ı���AECF�����Σ�
�⣺��1�����룺��l��ACʱ���ı���AECF�����Σ�
��ͼ1������AF��CE��
���ı���ABCD��ƽ���ı��Σ�
��OA=OC��AB��CD��
���FCO=��EAO��
�֡ߡ�FOC=��EOA��
���COF�ա�AOE��
��OE=OF��
��AC��EF��
���ı���AECF�����Σ�
��2���١��ı���ABCD�Ǿ��Σ�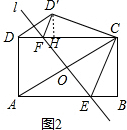
���ADC=90�㣬CD=AB=4��AD=BC=3��
��DF=xcm����CF=��4-x��cm��
���۵����ʿ�֪��
D��F=DF=x��CD��=AD=3����CD��F=��ADC=90�㣬
�ɹ��ɶ����ã�4-x��2=32+x2��
���x=$\frac{7}{8}$�� ��D��F=DF=$\frac{7}{8}$��
��D��F=DF=$\frac{7}{8}$��
��CF=4-$\frac{7}{8}$=$\frac{25}{8}$��
��ͼ2����D����D��H��CF��H���������ȿɵã�CF•D��H=D��F•CD�䣬
��D��H=$\frac{21}{25}$��
��S��DFD��=$\frac{1}{2}$��$\frac{7}{8}$��$\frac{21}{25}$=$\frac{147}{400}$��cm2��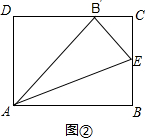
����ͼ�٣���BE=xcm��CE=��3-x��cm��AC=5cm��B��C=5-4=1cm��
���ݹ��ɶ����ɵ�B��C2+B��E2=CE2��
���x=$\frac{4}{3}$cm��
��ͼ�ڣ���BE=xcm����CE=��3-x��cm��AB��=4cm��B��E=xcm��
��Rt��ADB���У� �ɹ��ɶ����ɵ�BD��=$\sqrt{A{B}^{2}-A{D}^{2}}=\sqrt{16-9}=\sqrt{7}$cm��
�ɹ��ɶ����ɵ�BD��=$\sqrt{A{B}^{2}-A{D}^{2}}=\sqrt{16-9}=\sqrt{7}$cm��
B��C=��4-$\sqrt{7}$��cm��
��Rt��CB��E��B��C2+B��E2=CE2��
��16-8$\sqrt{7}$+7+x2=9-6x+x2��
���x=$\frac{16-4\sqrt{7}}{3}$cm��
��ͼ�ۣ�
���ı���ABEB����������ʱ����B�͵�B�����ֱ��AE�Գƣ���B��EC��ֱ�������Σ� ��ʱCE=1cm��BE=4cm��
��ʱCE=1cm��BE=4cm��
��ͼ��
BE=xcm��AB��=4cm��AD=3cm��CE=��x-3��cm��
��Rt��ADB����B��D=$\sqrt{AB{��}^{2}-A{D}^{2}}=\sqrt{16-9}=\sqrt{7}$cm��
B��C=$\sqrt{7}$+4��
��Rt��B��CE��7+8$\sqrt{7}$+16+x2-6x+9=x2��
���x=$\frac{16+4\sqrt{7}}{3}$cm��
���ϣ�BE�ij�Ϊ$\frac{4}{3}$cm��$\frac{16-4\sqrt{7}}{3}$cm��4cm��$\frac{16+4\sqrt{7}}{3}$cm��
���� ������Ҫ�����˼��α任���ۺ��⣬�����漰����֪ʶ�϶࣬���ε��ж������ɶ����������ε����ʡ��۵������ʺ�����������ļ��㣬���1������Ҫ�����������ε��ж����������2����������DH���ǹؼ����ڣ�2�����С����Ҫ�������ۣ�������©�⣬�����ѶȽϴ�


 �ʰ�Ӣ��ͬ����ϰ��ϵ�д�
�ʰ�Ӣ��ͬ����ϰ��ϵ�д� ѧϰʵ����ϵ�д�
ѧϰʵ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{2}{x}$$\sqrt{x-a}$ | B�� | $\frac{2a}{{x}^{2}}$$\sqrt{x-a}$ | C�� | 2ax4$\sqrt{x-a}$ | D�� | $\frac{2a}{x}$$\sqrt{x-a}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
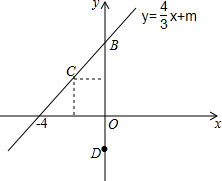 ��ͼ����֪һ�κ���y=$\frac{4}{3}$x+m��ͼ����x�ύ��A��-6��0������y���ڵ�B��
��ͼ����֪һ�κ���y=$\frac{4}{3}$x+m��ͼ����x�ύ��A��-6��0������y���ڵ�B���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
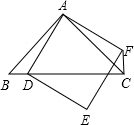 ��ͼ��ʾ���ı���ADEFΪ�����Σ���ABCΪ����ֱ�������Σ�D��BC���ϣ�����CF��
��ͼ��ʾ���ı���ADEFΪ�����Σ���ABCΪ����ֱ�������Σ�D��BC���ϣ�����CF���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com