已知如图 1 在△abc ∠acb=90 ac=1 ∠b=30 ce⊥ab答案解析
科目:czsx
来源:
题型:
已知△ABC中,点E为边AB的中点,将△ABC沿CE所在的直线折叠得△AEC,BF∥AC,交直线A′C于F.
(1)若∠ACB=90°,∠A=30°,求证:AC=CF+BF.
(2)若∠ACB为任意角,在图(2)图(3)的情况下分别写出AC、CF、BF之间关系,并证明图(3)结论.
(3)如图(4),若∠ACB=120°,BF=6,BC=4,则AC的长为
.

查看答案和解析>>
科目:czsx
来源:
题型:解答题
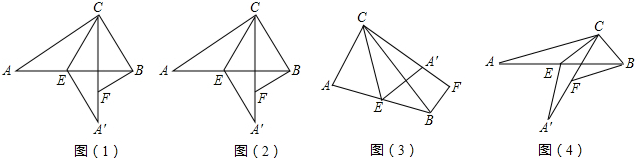
已知△ABC中,点E为边AB的中点,将△ABC沿CE所在的直线折叠得△AEC,BF∥AC,交直线A′C于F.
(1)若∠ACB=90°,∠A=30°,求证:AC=CF+BF.
(2)若∠ACB为任意角,在图(2)图(3)的情况下分别写出AC、CF、BF之间关系,并证明图(3)结论.
(3)如图(4),若∠ACB=120°,BF=6,BC=4,则AC的长为______.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
15.如图,已知△ABC中,∠ACB=90°,∠ABC=30°,AC=2,点P是边AB上的一个动点,以点P为圆心,PB的长为半径画弧,交射线BC于点D,射线PD交射线AC于点E.
(1)当点D与点C重合时,求PB的长;
(2)当点E在AC的延长线上时,设PB=x,CE=y,求y关于x的函数关系式,并写出定义域;
(3)当△PAD是直角三角形时,求PB的长.

查看答案和解析>>
科目:czsx
来源:
题型:解答题
16.已知△ABC中,点E为边AB的中点,将△AEC沿CE所在的直线折叠得△A′EC,BF∥AC,交直线A′C于F.
(1)如图(1),若∠ACB=90°,∠A=30°,BC=$\sqrt{3}$,求A′F的长.
(2)如图(2),若∠ACB为任意角,已知A′F=a,求BF的长(用a表示)
(3)如图(3),若∠ACB为任意角,猜想出AC、CF、BF之间的数量关系:AC=CF-BF,并说明理由.
(4)如图(4),若∠ACB=120°,BF=8,BC=5,则AC的长为15.

查看答案和解析>>
科目:czsx
来源:
题型:解答题
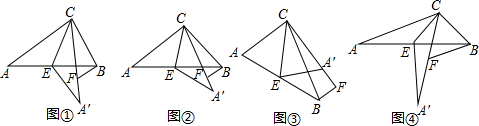
4.已知△ABC中,点E为边AB的中点,将△ABC沿CE所在的直线折叠得△A′EC,BF∥AC,交直线A′C于F.
(1)如图①,若∠ACB=90°,∠A=30°,BC=$\sqrt{3}$,求A′F的长;
(2)如图②,若∠ACB为任意角,已知A′F=a,求BF的长(用a表示);
(3)如图③,若∠ACB为任意角,猜想出AC、CF、BF之间的数量关系:AC=CF-BF,并说明理由;
(4)如图④,若∠ACB=120°,BF=8,BC=6,则AC的长为8+2$\sqrt{13}$..
查看答案和解析>>
科目:czsx
来源:
题型:
(2011•和平区模拟)已知,在Rt△ABC中,∠ACB=90°,点D、E分别在边AB、AC上,连接DE并延长,交BC的延长线于点P.
(1)如图①,当∠B=∠DPB=30°时,连接AP,若△AEP与△BDP相似,AE=1,求CE的长.
(2)如图②,若AD=AE=1,CE=2,BD=BC,求CP的长.
(3)如图③,若AD=AE=1,tan
∠BPD=,设CE=x,△ABC的周长为y,求y关于x的函数解析式.

查看答案和解析>>
科目:czsx
来源:2011年天津市和平区九年级结课考试数学试卷(解析版)
题型:解答题
已知,在Rt△ABC中,∠ACB=90°,点D、E分别在边AB、AC上,连接DE并延长,交BC的延长线于点P.
(1)如图①,当∠B=∠DPB=30°时,连接AP,若△AEP与△BDP相似,AE=1,求CE的长.
(2)如图②,若AD=AE=1,CE=2,BD=BC,求CP的长.
(3)如图③,若AD=AE=1,tan

,设CE=x,△ABC的周长为y,求y关于x的函数解析式.

查看答案和解析>>







 ,设CE=x,△ABC的周长为y,求y关于x的函数解析式.
,设CE=x,△ABC的周长为y,求y关于x的函数解析式.