如图,已知在平行四边形abcd中,ef平行ab交bc于e,交ad于f,连接ae,bf交于点m,连接答案解析

12．【定义】
若一个四边形恰好关于其中一条对角线所在的直线对称，则我们将这个四边形叫做镜面四边形．
【理解】
（1）下列说法是否正确（对的打“√”，错的打“×”）．
①平行四边形是一个镜面四边形．（×　）
②镜面四边形的面积等于对角线积的一半．（√　）
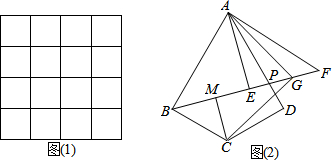
（2）如图（1），请你在4×4的网格（每个小正方形的边长为1）中画出一个镜面四边形，使它图（1）的顶点在格点上，且有一边长为$\sqrt{5}$．
【应用】
（3）如图（2），已知镜面四边形ABCD，∠BAD=60°，∠ABC=90°，AB≠BC，P是AD上一点，AE丄BP于E，在BP的延长线上取一点F，使EF=BE，连接AF，作∠FAD的平分线AG交BF于G，CM丄BF于M，连接CG．
①求∠EAG的度数．
②比较BM与EG的大小，并说明理由．
③若以线段CB，CG，AG为边构成的三角形是直角三角形，求cos∠CBM的值（直接写出答案）．

13．问题呈现：
如图1，点E、F、G、H分别在矩形ABCD的边AB、BC、CD、DA上，AE=DG，求证：2S_{四边形EFGH}=S_矩形ABCD．（S表示面积）
实验探究：
某数学实验小组发现：若图1中AH≠BF，点G在CD上移动时，上述结论会发生变化，分别过点E、G作BC边的平行线，再分别过点F、H作AB边的平行线，四条平行线分别相交于点A₁、B₁、C₁、D₁，得到矩形A₁B₁C₁D₁．
如图2，当AH＞BF时，若将点G向点C靠近（DG＞AE），经过探索，发现：2S_{四边形EFGH}=S_矩形ABCD+S${\;}_{矩形{A}_{1}{B}_{1}{C}_{1}{D}_{1}}$．
如图3，当AH＞BF时，若将点G向点D靠近（DG＜AE），请探索S_{四边形EFGH}、S_矩形ABCD与S${\;}_{矩形{A}_{1}{B}_{1}{C}_{1}{D}_{1}}$之间的数量关系，并说明理由．
迁移应用：
请直接应用“实验探究”中发现的结论解答下列问题：
（1）如图4，点E、F、G、H分别是面积为25的正方形ABCD各边上的点，已知AH＞BF，AE＞DG，S_{四边形EFGH}=11，HF=$\sqrt{29}$，求EG的长．
（2）如图5，在矩形ABCD中，AB=3，AD=5，点E、H分别在边AB、AD上，BE=1，DH=2，点F、G分别是边BC、CD上的动点，且FG=$\sqrt{10}$，连接EF、HG，请直接写出四边形EFGH面积的最大值．