
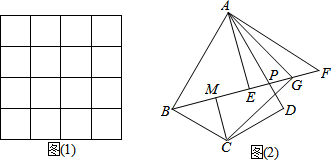
���� ��1������ƽ���ı��ε����ʺ;����ı��εĶ��壬ֱ���жϣ�
��2���ɾ����ı��ε����壬�õ�����������$\sqrt{5}$��һ��ֱ�ǣ�����ͼ�μ���
��3���ٸ��ݽ�ƽ���ߵĶ���õ���EAF=$\frac{1}{2}$��BAF����GAF=$\frac{1}{2}$��FAD���㣻�����жϡ�ABE�ס�BCM��ͨ�������жϳ�BM=EG���۷����������AG��CGΪб�ߣ����ù��ɶ������㼴�ɣ�
��� �⣺��1���١�ƽ���ı��β������κ�һ���Խ��߶Գƣ�
�����
�ʴ𰸡���
�ڡ߾����ı��ι��ڶԽ��߶Գƣ�
�ྵ���ı��ε������Խ����ഹֱ��
�ྵ���ı��ε�������ڶԽ�����һ�룻
�ʴ�Ϊ�̣�
��2����ͼ1
����һ�߳�Ϊ$\sqrt{5}$��
�ྵ���ı��α���������$\sqrt{5}$��
��3���١�AE��BP��EF=BE��
��AB=AF��
���EAF=$\frac{1}{2}$��BAF��
�ߡ�GAF=$\frac{1}{2}$��FAD��
���EAG=��EAF-��GAF=$\frac{1}{2}$��BAF-$\frac{1}{2}$��FAD=$\frac{1}{2}$��BAD=30�㣻
��BM=EG��
�������£�����AC��
�ߡ�ABC=90�㣬
��AB=$\sqrt{3}$BC��
�ߡ�ABC=��AEB=��CMB=90�㣬
���BAE+��ABF=��ABP+��ABF=90�㣬
���BAE=��CBF��
���ABE�ס�BCM��
��$\frac{AE}{BM}$=$\frac{AB}{AC}$=$\sqrt{3}$��
��AE=$\sqrt{3}$BM��
�ߡ�EAG=30�㣬AE��BP��
��AE=$\sqrt{3}$EG��
��BM=EG��
��cos��CBM=$\frac{\sqrt{6}}{4}$��$\frac{\sqrt{10}}{4}$
��BM=x��BC=y��
��CM=$\sqrt{{y}^{2}-{x}^{2}}$��
�ߡ�ABE�ס�BCM��
��$\frac{AE}{BM}=\frac{AB}{AC}=\frac{BE}{CM}$=$\sqrt{3}$��
��AE=$\sqrt{3}$BM��AB=$\sqrt{3}$BC=$\sqrt{3}$y��BE=$\sqrt{3}$y=$\sqrt{3��{y}^{2}-{x}^{2}��}$��
��BG=BE+EG=$\sqrt{3��{y}^{2}-{x}^{2}��}$+x��
��EG=BM=x
MG=BE=y=$\sqrt{3��{y}^{2}-{x}^{2}��}$��
��CG=$\sqrt{M{C}^{2}+M{G}^{2}}$=2$\sqrt{{y}^{2}-{x}^{2}}$��
��AE��BP����EAG=30�㣬
��AG=2EG=2x��
�������AG��BC��
���߶�CB��CG��AGΪ�߹��ɵ���������ֱ�������Σ�ֻ������AGΪб��CGΪб�ߣ�
��AGΪб�ߣ�
��CB2+CG2=AG2��
��y2+��2$\sqrt{{y}^{2}-{x}^{2}}$��2=��2x��2��
��y=$\frac{2\sqrt{10}}{5}$x��y=-$\frac{2\sqrt{10}}{5}$x���ᣩ��
��BM=x��BC=y=$\frac{2\sqrt{10}}{5}$x��
��cos��CBM=$\frac{BM}{BC}$=$\frac{\sqrt{10}}{4}$��
��CGΪб�ߣ�
��CB2+AG2=CG2��
��y2+��2x��2=��2$\sqrt{{y}^{2}-{x}^{2}}$��2��
��y=$\frac{2\sqrt{6}}{3}$x��y=-$\frac{2\sqrt{6}}{3}$x���ᣩ��
��BC=y=$\frac{2\sqrt{6}}{3}$x��BM=x��
��cos��CBM=$\frac{BM}{BC}$=$\frac{\sqrt{6}}{4}$��
cos��CBM=$\frac{\sqrt{6}}{4}$��$\frac{\sqrt{10}}{4}$��
���� �������ı����ۺ��⣬��Ҫ������ƽ���ı��ε����ʣ���ƽ���ߵ����壬�����������ж������ʣ����ɶ�����������Ǻ��������ù��ɶ��������Ʊ�ʾ�߶����籾��Ĺؼ���Ҳ���ѵ㣮


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a+a2=a3 | B�� | a6b��a2=a3b | C�� | ��a-b��2=a2-b2 | D�� | ��-ab3��2=a2b6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ������ֱ�����ǰ�Ķ���A��C�ֱ���ֱ��a��b�ϣ���a��b����1=35�㣬���2�Ķ���Ϊ��������
��ͼ������ֱ�����ǰ�Ķ���A��C�ֱ���ֱ��a��b�ϣ���a��b����1=35�㣬���2�Ķ���Ϊ��������| A�� | 35�� | B�� | 15�� | C�� | 10�� | D�� | 5�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
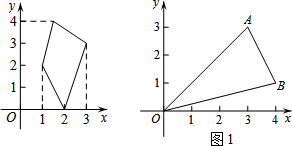
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
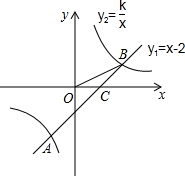 ��ͼ��һ�κ���y1=x-2��ͼ���뷴��������y2=$\frac{k}{x}$��ͼ���ཻ��A��B���㣬��x���ཻ�ڵ�C����֪tan��BOC=$\frac{1}{2}$����B������Ϊ��m��n�������������Ľ���ʽ��
��ͼ��һ�κ���y1=x-2��ͼ���뷴��������y2=$\frac{k}{x}$��ͼ���ཻ��A��B���㣬��x���ཻ�ڵ�C����֪tan��BOC=$\frac{1}{2}$����B������Ϊ��m��n�������������Ľ���ʽ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ƽ��ֱ������ϵ�У��������¶��壺����y=��x-m����x-m+1����y=��x-m����x-m-1�����������κ�����ͼ������ֵ������ߣ�
��ƽ��ֱ������ϵ�У��������¶��壺����y=��x-m����x-m+1����y=��x-m����x-m-1�����������κ�����ͼ������ֵ������ߣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -$\frac{3}{2}$ | B�� | $\frac{3}{2}$ | C�� | -$\frac{2}{3}$ | D�� | $\frac{2}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ABΪ��Oֱ����BCΪ��O���ߣ��е�ΪB��COƽ������AD����ֱ��DC��
ABΪ��Oֱ����BCΪ��O���ߣ��е�ΪB��COƽ������AD����ֱ��DC���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com