
科目:czsx 来源: 题型:
| 班级 | 行为规范 | 学习成绩 | 校运动会 | 艺术获奖 | 劳动卫生 |
| 八(1)班 | 10 | 10 | 6 | 10 | 7 |
| 八(4)班 | 10 | 8 | 8 | 9 | 8 |
| 八(8)班 | 9 | 10 | 9 | 6 | 9 |
科目:czsx 来源:浙教版(2014) 八年级下 题型:
| |||||
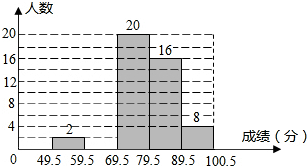
科目:czsx 来源:2014年初中毕业升学考试(四川雅安卷)数学(解析版) 题型:解答题
某老师对本班所有学生的数学考试成绩(成绩为整数,满分为100分)作了统计分析,绘制成如下频数、频率分布表和频数分布直方图,请你根据图表提供的信息,解答下列问题:

分组 | 49.5~59.5 | 59.5~69.5 | 69.5~79.5 | 79.5~89.5 | 89.5~100.5 |
频数 | 2 | a | 20 | 16 | 8 |
频率 | 0.04 | 0.08 | 0.40 | 0.32 | b |
(1)求a,b的值;
(2)补全频数分布直方图;
(3)老师准备从成绩不低于80分的学生中选1人介绍学习经验,那么被选中的学生其成绩不低于90分的概率是多少?
科目:czsx 来源: 题型:解答题
| 班级 | 行为规范 | 学习成绩 | 校运动会 | 艺术获奖 | 劳动卫生 |
| 八(1)班 | 10 | 10 | 6 | 10 | 7 |
| 八(4)班 | 10 | 8 | 8 | 9 | 8 |
| 八(8)班 | 9 | 10 | 9 | 6 | 9 |
科目:czsx 来源:南昌 题型:解答题
| 班级 | 行为规范 | 学习成绩 | 校运动会 | 艺术获奖 | 劳动卫生 |
| 八(1)班 | 10 | 10 | 6 | 10 | 7 |
| 八(4)班 | 10 | 8 | 8 | 9 | 8 |
| 八(8)班 | 9 | 10 | 9 | 6 | 9 |
科目:czsx 来源:期末题 题型:解答题

科目:czsx 来源:期末题 题型:解答题

科目:czsx 来源:第2章《数据的离散程度》常考题集(06):2.2 方差与标准差(解析版) 题型:解答题
| 班级 | 行为规范 | 学习成绩 | 校运动会 | 艺术获奖 | 劳动卫生 |
| 八(1)班 | 10 | 10 | 6 | 10 | 7 |
| 八(4)班 | 10 | 8 | 8 | 9 | 8 |
| 八(8)班 | 9 | 10 | 9 | 6 | 9 |
科目:czsx 来源: 题型:
| 分组 | 49.5~59.5 | 59.5~69.5 | 69.5~79.5 | 79.5~89.5 | 89.5~100.5 |
| 频数 | 2 | a | 20 | 16 | 8 |
| 频率 | 0.04 | 0.08 | 0.40 | 0.32 | b |
科目:czsx 来源: 题型:
某老师对本班所有学生的数学考试成绩(成绩为整数,满分为100分)作了统计分析,绘制成如下频数、频率分布表和频数分布直方图,请你根据图表提供的信息,解答下列问题:
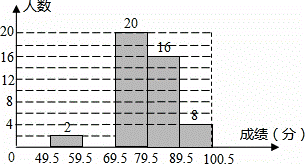
| 分组 | 49.5~59.5 | 59.5~69.5 | 69.5~79.5 | 79.5~89.5 | 89.5~100.5 |
| 频数 | 2 | a | 20 | 16 | 8 |
| 频率 | 0.04 | 0.08 | 0.40 | 0.32 | b |
(1)求a,b的值;
(2)补全频数分布直方图;
(3)老师准备从成绩不低于80分的学生中选1人介绍学习经验,那么被选中的学生其成绩不低于90分的概率是多少?
科目:czsx 来源: 题型:
某学校准备从八年级⑴、⑷、⑻班这三个班中推荐一个班为市级先进班集体的候选班,现对 这三个班进行综合素质考评,下表是它们五项素质考评的得分表(以分为单位,每项满分为10分)
这三个班进行综合素质考评,下表是它们五项素质考评的得分表(以分为单位,每项满分为10分)
| 班 级 | 行为 规范 | 学习 成绩 | 校运 运会 | 艺术 获奖 | 劳动 卫生 |
| 八⑴班 | 10 | 10 | 6 | 10 | 7 |
| 八⑷班 | 10 | 8 | 8 | 9 | 8 |
| 八⑻班 | 9 | 10 | 9 | 6 | 9 |
⑴请问各班五项考评分的平均数、中位数和众中哪个统计量不能反映三个班的考评结果的差异?并从中选择一个能反映差异的统计量将他们得分进行排序;
⑵根据你对表中五个项目的重要程度的认识,设定一个各项考评内容的占分比例(比例的各项须满足:①均为整数;②总和为10;③不全相同),按这个比例对各班的得分重新计算,比较出大小关系,并从中推荐一个得分最高的班级作为市级先进班集体的候选班.
科目:czsx 来源:2014-2015学年江苏省无锡市九年级中考一模数学试卷(解析版) 题型:解答题
(本题满分10分)某校校园超市老板到批发中心选购甲、乙两种品牌的文具盒,乙品牌的进货单价是甲品牌进货单价的2倍,考虑各种因素,预计购进乙品牌文具盒的数量y(个)与甲品牌文具盒的数量x(个)之间的函数关系如图所示.当购进的甲、乙品牌的文具盒中,甲有120个时,购进甲、乙品牌文具盒共需7200元.
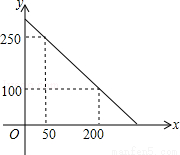
(1)根据图象,求y与x之间的函数关系式;
(2)求甲、乙两种品牌的文具盒进货单价;
(3)若该超市每销售1个甲种品牌的文具盒可获利4元,每销售1个乙种品牌的文具盒可获利9元,根据学生需求,超市老板决定,准备用不超过6300元购进甲、乙两种品牌的文具盒,且这两种品牌的文具盒全部售出后获利不低于1795元,问该超市有几种进货方案?哪种方案能使获利最大?最大获利为多少元?
科目:czsx 来源:2014-2015学年江苏省无锡市九年级5月模拟考试数学试卷(解析版) 题型:解答题
(本题满分9分)为了调动同学们的学习积极性,某班班主任陈老师在班级管理中采用了奖励机制,每次期中期末考试后都会进行表彰奖励.期中考试后,陈老师花了300元购买甲、乙两种奖品用于奖励进步显著学生及成绩特别优秀学生.期末考试后,陈老师再次去购买奖品时,发现甲奖品每件上涨了6元,乙奖品每件上涨了12元,结果购买相同数量的甲、乙两种奖品却多花了120元.设陈老师每次购买甲奖品x件,乙奖品y件.
(1)请直接写出y与x之间的函数关系式: .
(2)若x=8,且这两种奖品不再调价.若陈老师再次去购买奖品,且所买甲奖品比前两次都少1件,则他最多买几件乙奖品,才能把奖品总费用控制在300元以内?
【备注:已知陈老师第一次购买奖品发现,甲奖品比乙奖品便宜,两种奖品单价(元)都在30以内且为偶数.】
科目:gzsx 来源: 题型:
(本小题满分12分)中央电视台《同一首歌》大型演唱会曾在我市湄洲岛举行,之前甲、乙两人参加大会青年志愿者的选拔.已知在备选的10道试题中,甲能答对其中的6题,乙能答对其中的8题。规定每次考试都从备选题中随机抽出3题进行测试,至少答对2题才能入选(两人独立答题)。(Ⅰ)求甲答对试题数ξ的概率分布(列表![]() )及数学期望;(Ⅱ)求甲、乙两人至少有一人入选的概率(设甲、乙两人考试合格的事件分别为A、B).
)及数学期望;(Ⅱ)求甲、乙两人至少有一人入选的概率(设甲、乙两人考试合格的事件分别为A、B).
科目:gzsx 来源: 题型:
(本小题满分13分)随着石油资源的日益紧缺,我国决定建立自己的石油储备基地,
已知某石油储备基地原储有石油![]() 吨,按计划正式运营后的第一年进油量为已储油量的25%,以后每年的进油量均为上一年底储油量的25%,且每年年内用出
吨,按计划正式运营后的第一年进油量为已储油量的25%,以后每年的进油量均为上一年底储油量的25%,且每年年内用出![]() 吨,设
吨,设![]() 为正式运营后第
为正式运营后第![]() 年年底的石油储量.(Ⅰ)求
年年底的石油储量.(Ⅰ)求![]() 、
、![]() 、
、![]() ; (Ⅱ)猜测出
; (Ⅱ)猜测出![]() 的表达式并用数学归纳法予以证明;(Ⅲ)为抵御突发事件,该油库年底储油量不得少于
的表达式并用数学归纳法予以证明;(Ⅲ)为抵御突发事件,该油库年底储油量不得少于![]() 吨,如果
吨,如果![]() 吨,该油库能否长期按计划运营?如果能,请加以证明;如果不能,请说明理由.(计算中可供参考的数据:
吨,该油库能否长期按计划运营?如果能,请加以证明;如果不能,请说明理由.(计算中可供参考的数据:![]() ,
,![]() )
)
科目:gzsx 来源:2012-2013学年安徽省高三第一次质量检测理科数学试卷(解析版) 题型:解答题
(本小题满分12分)
某高校设计了一个实验学科的实验考查方案:考生从6道备选题中一次性随机抽取3题,按照题目要求独立完成全部实验操作。规定:至少正确完成其中2题的便可提交通过。已知6道备选题中考生甲有4道题能正确完成,2道题不能完成;考生乙每题正确完成的概率都是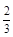 ,且每题正确完成与否互不影响。
,且每题正确完成与否互不影响。
(Ⅰ)分别写出甲、乙两考生正确完成题数的概率分布列,并计算数学期望;
(Ⅱ)试从两位考生正确完成题数的数学期望及至少正确完成2题的概率分析比较两位考生的实验操作能力.
科目:gzsx 来源:2011-2012学年内蒙古呼伦贝尔市高三第三次模拟考试理科数学试卷 题型:解答题
(本小题满分12分)为了解今年某校高三毕业班准备报考飞行员学生的体重情
况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前 个小组的频率之比为
个小组的频率之比为 ,其中第
,其中第 小组的频数为
小组的频数为 .
.
(1)求该校报考飞行员的总人数;
(2)以这所学校的样本数据来估计全省的总体数据,若从全省报考飞行员的同学中(人数很多)任选三人,设X表示体重超过60公斤的学生人数,求X的分布列和数学期望.

科目:gzsx 来源:2010年延安市高二下学期期末考试(理科)数学卷 题型:解答题
(本小题满分12分)某省份今年是新课标高考的第一年,某校为了充分了解新课标高考,数学备课组从过去2年的新课标各地模拟卷中挑选出50份试卷进行研究,各地挑选的试卷数如下表所示:
|
地区 |
地区A |
地区B |
地区C |
地区D |
|
试卷数 |
20 |
15 |
5 |
10 |
(1)从这50份试卷中随机选出2份,求2份试卷选自同一地区的概率;
(2)若从C、D两地区挑选出2份试卷进行研究,设挑选出地区C的试卷数为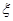 ,求随机变量
,求随机变量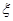 的分布列和数学期望。
的分布列和数学期望。
科目:gzsx 来源:陕西省2009-2010学年度第二学期期末考试高二数学(理科)试题 题型:解答题
(本小题满分10分)
某省份今年是新课标高考的第一年,某校为了充分了解新课标高考,数学备课组从过去2年的新课标各地模拟卷中挑选出50份试卷进行研究,各地挑选的试卷数如下表所示:
|
地区 |
地区A |
地区B |
地区C |
地区D |
|
试卷数 |
20 |
15 |
5 |
10 |
(1)从这50份试卷中随机选出2份,求2份试卷选自同一地区的概率;
(2)若从C、D两地区挑选出2份试卷进行研究,设挑选出地区C的试卷数为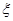 ,求随机变量
,求随机变量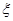 的分布列和数学期望。
的分布列和数学期望。
科目:gzsx 来源: 题型:解答题
(本小题满分12分)
某高校设计了一个实验学科的实验考查方案:考生从6道备选题中一次性随机抽取3题,按照题目要求独立完成全部实验操作。规定:至少正确完成其中2题的便可提交通过。已知6道备选题中考生甲有4道题能正确完成,2道题不能完成;考生乙每题正确完成的概率都是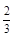 ,且每题正确完成与否互不影响。
,且每题正确完成与否互不影响。
(Ⅰ)分别写出甲、乙两考生正确完成题数的概率分布列,并计算数学期望;
(Ⅱ)试从两位考生正确完成题数的数学期望及至少正确完成2题的概率分析比较两位考生的实验操作能力.