精英家教网 >
试题搜索列表 >已知0(0,0),A(2,-1),B(1,3),向量OP=向量OA+t乘以向量OB,若四点O,A,B,P是平行四边形的四个顶点,则实数t=
已知0(0,0),A(2,-1),B(1,3),向量OP=向量OA+t乘以向量OB,若四点O,A,B,P是平行四边形的四个顶点,则实数t=答案解析
科目:gzsx
来源:
题型:
16、已知△ABC的三个顶点分别为A(2,4),B(-1,2),C(1,0).
(1)求△ABC三条边所在直线的方程;
(2)若点P(x,y)在△ABC内部及边界运动,求z=x-y的最大、最小值.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知△OAB的顶点坐标为O(0,0),A(2,9),B(6,-3),点P的横坐标为14,且
=λ,点Q是边AB上一点,且
•=0.
(1)求实数λ的值与点P的坐标;
(2)求点Q的坐标;
(3)若R为线段OQ上的一个动点,试求
•(+)的取值范围.
查看答案和解析>>
科目:gzsx
来源:0103 期末题
题型:解答题
已知△OAB的顶点坐标为O(0,0),A(2,9),B(6,-3), 点P的横坐标为14,且

,点Q是边AB上一点,且

。
(Ⅰ)求实数λ的值与点P的坐标;
(Ⅱ)求点Q的坐标。
查看答案和解析>>
科目:gzsx
来源:不详
题型:解答题
已知△ABC的三个顶点分别为A(2,4),B(-1,2),C(1,0).
(1)求△ABC三条边所在直线的方程;
(2)若点P(x,y)在△ABC内部及边界运动,求z=x-y的最大、最小值.
查看答案和解析>>
科目:gzsx
来源:2010-2011学年江苏省苏州市常熟市高一(上)期末数学模拟试卷(解析版)
题型:解答题
已知△OAB的顶点坐标为O(0,0),A(2,9),B(6,-3),点P的横坐标为14,且
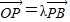
,点Q是边AB上一点,且

.
(1)求实数λ的值与点P的坐标;
(2)求点Q的坐标;
(3)若R为线段OQ上的一个动点,试求

的取值范围.
查看答案和解析>>
科目:gzsx
来源:不详
题型:解答题
已知△OAB的顶点坐标为O(0,0),A(2,9),B(6,-3),点P的横坐标为14,且
=λ,点Q是边AB上一点,且
•=0.
(1)求实数λ的值与点P的坐标;
(2)求点Q的坐标;
(3)若R为线段OQ上的一个动点,试求
•(+)的取值范围.
查看答案和解析>>
科目:gzsx
来源:
题型:解答题
已知△OAB的顶点坐标为O(0,0),A(2,9),B(6,-3),点P的横坐标为14,且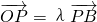 ,点Q是边AB上一点,且
,点Q是边AB上一点,且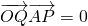 .
.
(1)求实数λ的值与点P的坐标;
(2)求点Q的坐标;
(3)若R为线段OQ上的一个动点,试求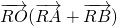 的取值范围.
的取值范围.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知平行四边形ABCD的三个顶点A(-2,1),B(-1,3),C(3,4),则第四个顶点D的坐标为( )
查看答案和解析>>
科目:gzsx
来源:
题型:
(2012•上饶一模)已知抛物线W:y=ax2经过点A(2,1),过A作倾斜角互补的两条不同的直线L1,L2.
(1)求抛物线W的方程及其准线方程;
(2)当直线L1与抛物线W相切时,求直线L2与抛物线W所围成封闭区域的面积;
(3)设直线L1、L2分别交抛物线W于B、C两点(均不与A重合),若以BC为直径的圆与抛物线的准线相切,求直线BC的方程.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知抛物线W:y=ax2经过点A(2,1),过A作倾斜角互补的两条不同直线l1,l2.
(Ⅰ)求抛物线W的方程及准线方程;
(Ⅱ)当直线l1与抛物线W相切时,求直线l2的方程
(Ⅲ)设直线l1,l2分别交抛物线W于B,C两点(均不与A重合),若以线段BC为直径的圆与抛物线的准线相切,求直线BC的方程.
查看答案和解析>>
科目:gzsx
来源:2012年江西省上饶市高考数学一模试卷(理科)(解析版)
题型:解答题
已知抛物线W:y=ax2经过点A(2,1),过A作倾斜角互补的两条不同的直线L1,L2.
(1)求抛物线W的方程及其准线方程;
(2)当直线L1与抛物线W相切时,求直线L2与抛物线W所围成封闭区域的面积;
(3)设直线L1、L2分别交抛物线W于B、C两点(均不与A重合),若以BC为直径的圆与抛物线的准线相切,求直线BC的方程.
查看答案和解析>>
科目:gzsx
来源:2005-2006学年江苏省扬州市高一(上)期末数学试卷(解析版)
题型:选择题
已知平行四边形ABCD的三个顶点A(-2,1),B(-1,3),C(3,4),则第四个顶点D的坐标为( )
A.(1,1)
B.(2,4)
C.(2,2)
D.(4,4)
查看答案和解析>>
科目:gzsx
来源:2009-2010学年北京市海淀区高三(上)期末数学试卷(理科)(解析版)
题型:解答题
已知抛物线W:y=ax2经过点A(2,1),过A作倾斜角互补的两条不同直线l1,l2.
(Ⅰ)求抛物线W的方程及准线方程;
(Ⅱ)当直线l1与抛物线W相切时,求直线l2的方程
(Ⅲ)设直线l1,l2分别交抛物线W于B,C两点(均不与A重合),若以线段BC为直径的圆与抛物线的准线相切,求直线BC的方程.
查看答案和解析>>
科目:gzsx
来源:重难点手册 高中数学·必修4(配人教A版新课标) 人教A版新课标
题型:044
如下图,已知平面上三点坐标分别为A(-2,1),B(-1,3),C(3,4).求D的坐标,使得这四点构成一个平行四边形.

查看答案和解析>>
科目:gzsx
来源:
题型:解答题
已知抛物线W:y=ax2经过点A(2,1),过A作倾斜角互补的两条不同的直线L1,L2.
(1)求抛物线W的方程及其准线方程;
(2)当直线L1与抛物线W相切时,求直线L2与抛物线W所围成封闭区域的面积;
(3)设直线L1、L2分别交抛物线W于B、C两点(均不与A重合),若以BC为直径的圆与抛物线的准线相切,求直线BC的方程.
查看答案和解析>>
科目:gzsx
来源:2010-2011学年湖南省张家界市高三联考数学试卷1(理科)(解析版)
题型:解答题
已知抛物线W:y=ax2经过点A(2,1),过A作倾斜角互补的两条不同直线l1,l2.
(Ⅰ)求抛物线W的方程及准线方程;
(Ⅱ)当直线l1与抛物线W相切时,求直线l2的方程
(Ⅲ)设直线l1,l2分别交抛物线W于B,C两点(均不与A重合),若以线段BC为直径的圆与抛物线的准线相切,求直线BC的方程.
查看答案和解析>>
科目:gzsx
来源:2010-2011学年湖南省衡阳市高三联考数学试卷1(理科)(解析版)
题型:解答题
已知抛物线W:y=ax2经过点A(2,1),过A作倾斜角互补的两条不同直线l1,l2.
(Ⅰ)求抛物线W的方程及准线方程;
(Ⅱ)当直线l1与抛物线W相切时,求直线l2的方程
(Ⅲ)设直线l1,l2分别交抛物线W于B,C两点(均不与A重合),若以线段BC为直径的圆与抛物线的准线相切,求直线BC的方程.
查看答案和解析>>
科目:gzsx
来源:高考数学最后冲刺必读题解析30讲(29)(解析版)
题型:解答题
已知抛物线W:y=ax2经过点A(2,1),过A作倾斜角互补的两条不同直线l1,l2.
(Ⅰ)求抛物线W的方程及准线方程;
(Ⅱ)当直线l1与抛物线W相切时,求直线l2的方程
(Ⅲ)设直线l1,l2分别交抛物线W于B,C两点(均不与A重合),若以线段BC为直径的圆与抛物线的准线相切,求直线BC的方程.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知函数f(x)=4x2-4ax+a2-2a+2
(1)当a=0时,求f(x)=4x2-4ax+a2-2a+2在区间[0,2]上的最大值和最小值.
(2)若函数f(x)=4x2-4ax+a2-2a+2在区间[0,2]上的最小值为3,求实数a的值.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知曲线y=2x-x2上有两点A(2,0),B(1,1),求:
(1)割线AB的斜率kAB;
(2)点A处的切线的方程;
(3)过点A的切线斜率kAT.
查看答案和解析>>

 ,点Q是边AB上一点,且
,点Q是边AB上一点,且 。
。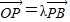 ,点Q是边AB上一点,且
,点Q是边AB上一点,且 .
. 的取值范围.
的取值范围.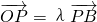 ,点Q是边AB上一点,且
,点Q是边AB上一点,且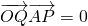 .
.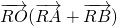 的取值范围.
的取值范围.