
科目:czsx 来源:《20.7 反比例函数的图象、性质和应用》2010年同步试卷(解析版) 题型:解答题
 ,分别根据下列条件求出字母k的取值范围:(1)函数图象位于第一、三象限;(2)在每一象限内,y随x的增大而增大.
,分别根据下列条件求出字母k的取值范围:(1)函数图象位于第一、三象限;(2)在每一象限内,y随x的增大而增大.科目:czsx 来源: 题型:解答题
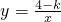 ,分别根据下列条件求出字母k的取值范围:(1)函数图象位于第一、三象限;______(2)在每一象限内,y随x的增大而增大.______
,分别根据下列条件求出字母k的取值范围:(1)函数图象位于第一、三象限;______(2)在每一象限内,y随x的增大而增大.______科目:czsx 来源:《23.6 反比例函数》2009年同步练习1(解析版) 题型:填空题
 ,分别根据下列条件求出字母k的取值范围:(1)函数图象位于第一、三象限; (2)在每一象限内,y随x的增大而增大.
,分别根据下列条件求出字母k的取值范围:(1)函数图象位于第一、三象限; (2)在每一象限内,y随x的增大而增大. 科目:czsx 来源:不详 题型:解答题
| 4-k |
| x |
科目:czsx 来源:不详 题型:填空题
| 4-k |
| x |
科目:czsx 来源:2011-2012学年江苏盐城九年级中考模拟考试数学试卷(解析版) 题型:解答题
如图,抛物线经过 ,
, ,
, 三点.
三点.
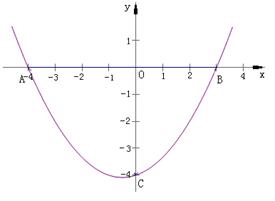
(1)求该抛物线的解析式;
(2)在该抛物线的对称轴上存在一点 ,使
,使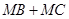 的值最小,求点
的值最小,求点 的坐标以
的坐标以
及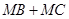 的最小值;
的最小值;
(3)在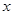 轴上取一点
轴上取一点 ,连接
,连接 .现有一动点
.现有一动点 以每秒
以每秒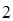 个单位长度的速度从点
个单位长度的速度从点 出发,沿线段
出发,沿线段 向点
向点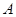 运动,运动时间为
运动,运动时间为 秒,另有一动点
秒,另有一动点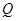 以某一速度同时从点
以某一速度同时从点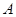 出发,沿线段
出发,沿线段 向点
向点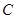 运动,当点
运动,当点 、点
、点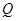 两点中有一点到达终点时,另一点则停止运动(如右图所示).在运动的过程中是否存在一个
两点中有一点到达终点时,另一点则停止运动(如右图所示).在运动的过程中是否存在一个 值,使线段
值,使线段 恰好被
恰好被 垂直平分.如果存在,请求出
垂直平分.如果存在,请求出 的值和点
的值和点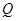 的速度,如果不存在,请说明理由.
的速度,如果不存在,请说明理由.

【解析】此题主要考查了用待定系数法求二次函数解析式,以及利用函数图象和图象上点的性质判断符合某一条件的点是否存在,是一道开放性题目,有利于培养同学们的发散思维能力
科目:czsx 来源: 题型:022
用待定系数法求一次函数解析式的一般步骤是:
(1)设所求的一次函数解析式为___________,其中k,b是待确定的常数;
(2)把______对已知的自变量与函数的对应值分别代入_______,得到关于k,b的___________;
(3)解这个关于k,b的_________,求出k,b的值;
(4)把求得的k,b的值代入_______,就得到所求的一次函数解析式.
科目:czsx 来源: 题型:
| a | x |
科目:czsx 来源:2013年初中数学单元提优测试卷-反比例函数与一次函数的图像(解析版) 题型:填空题
已知正比例函数y=kx与反比例函数y= 相交于点A(1,b)、点B(c,﹣2),求k+a的值.甲同学说:未知数太多,很难求的;乙同学说:可能不是用待定系数法来求;丙说:如果用数形结合的方法,利用两交点在坐标系中位置的特殊性,可以试试.请结合他们的讨论求出k+a= .
相交于点A(1,b)、点B(c,﹣2),求k+a的值.甲同学说:未知数太多,很难求的;乙同学说:可能不是用待定系数法来求;丙说:如果用数形结合的方法,利用两交点在坐标系中位置的特殊性,可以试试.请结合他们的讨论求出k+a= .
科目:czsx 来源: 题型:阅读理解
甲船从A港出发顺流匀速驶向B港,行至某处,发现船上一救生圈不知何时落入水中,立刻原路返回,找到救生圈后,继续顺流驶向B港.乙船从B港出发逆流匀速驶向A港.已知救生圈漂流的速度和水流速度相同;甲、乙两船在静水中的速度相同.甲、乙两船到A港的距离y1、y2(km)与行驶时间x(h)之间的函数图象如图所示.
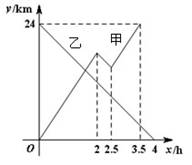
(1)写出乙船在逆流中行驶的速度(2)求甲船在逆流中行驶的路程.
(3)求甲船到A港的距离y1与行驶时间x之间的函数关系式
(4)求救生圈落入水中时,甲船到A港的距离.
【参考公式:船顺流航行的速度![]() 船在静水中航行的速度+水流速度,船逆流航行的速度
船在静水中航行的速度+水流速度,船逆流航行的速度![]() 船在静水中航行的速度
船在静水中航行的速度![]() 水流速度.】
水流速度.】
【解析】(1)由图可知,乙在4小时内走了24千米,根据路程=速度×时间,可得出其速度.
(2)由图可知2到2.5小时的过程中甲是逆流而行,这0.5小时内甲的速度何乙的速度相同,因此可得出甲走的路程
(3)要求距离首先要求出顺流的速度,可根据甲在0至2小时走的路程-2至2.5小时的路程+2.5至3.5小时的路程=24千米,求出顺流的速度,然后根据不同的x的范围,用待定系数法求出y与x的函数关系式.
(4)根据(3)求出的顺流的速度可求出水流的速度,然后根据船追救生圈的距离+救生圈顺水的距离=二者在掉落时间到追及时间拉开的距离.求出自变量的值,进而求出甲船到A港的距离.
科目:czsx 来源: 题型:
在平面直角坐标系中,一动点P(x,y)从M(1,0)出发,沿由A(-1,1),B(-1,-1),C(1,-1),D(1,1)四点组成的正方形边线(如图①)按一定方向运动.图②是P点运动的路程s(个单位)与运动时间![]() (秒)之间的函数图象,图③是P点的纵坐标y与P点运动的路程s之间的函数图象的一部分.
(秒)之间的函数图象,图③是P点的纵坐标y与P点运动的路程s之间的函数图象的一部分.
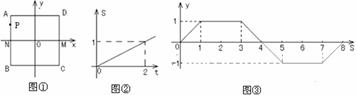
(1)s与t之间的函数关系式是: ;
(2)与图③相对应的P点的运动路径是: ;P点出发 秒首次到达点B;
(3)写出当3≤s≤8时,y与s之间的函数关系式,并在图③中补全函数图象.
解题思路:(1)由图②知,s与t是正比例函数关系,用“待定系数法”可求的关系式;(2)结合题意和图③的函数图象,P点的运动路径是:M→D→A→N;从(1)中知点P的运动速度,可以求出点P运动到点B需要的时间;(3)对3≤s≤8的范围,又需要分三个时间段分别求解.
科目:czsx 来源:2012年浙江省杭州市萧山区中考数学模拟试卷(2月份)(解析版) 题型:填空题
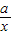 相交于点A(1,b)、点B(c,-2),求k+a的值.甲同学说:未知数太多,很难求的;乙同学说:可能不是用待定系数法来求;丙说:如果用数形结合的方法,利用两交点在坐标系中位置的特殊性,可以试试.请结合他们的讨论求出k+a= .
相交于点A(1,b)、点B(c,-2),求k+a的值.甲同学说:未知数太多,很难求的;乙同学说:可能不是用待定系数法来求;丙说:如果用数形结合的方法,利用两交点在坐标系中位置的特殊性,可以试试.请结合他们的讨论求出k+a= . 科目:czsx 来源:2011-2012学年江苏省无锡市中考模拟(5)数学卷(解析版) 题型:解答题
甲船从A港出发顺流匀速驶向B港,行至某处,发现船上一救生圈不知何时落入水中,立刻原路返回,找到救生圈后,继续顺流驶向B港.乙船从B港出发逆流匀速驶向A港.已知救生圈漂流的速度和水流速度相同;甲、乙两船在静水中的速度相同.甲、乙两船到A港的距离y1、y2(km)与行驶时间x(h)之间的函数图象如图所示.
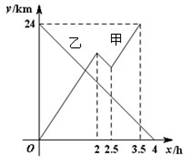
(1)写出乙船在逆流中行驶的速度(2)求甲船在逆流中行驶的路程.
(3)求甲船到A港的距离y1与行驶时间x之间的函数关系式
(4)求救生圈落入水中时,甲船到A港的距离.
【参考公式:船顺流航行的速度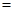 船在静水中航行的速度+水流速度,船逆流航行的速度
船在静水中航行的速度+水流速度,船逆流航行的速度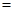 船在静水中航行的速度
船在静水中航行的速度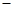 水流速度.】
水流速度.】
【解析】(1)由图可知,乙在4小时内走了24千米,根据路程=速度×时间,可得出其速度.
(2)由图可知2到2.5小时的过程中甲是逆流而行,这0.5小时内甲的速度何乙的速度相同,因此可得出甲走的路程
(3)要求距离首先要求出顺流的速度,可根据甲在0至2小时走的路程-2至2.5小时的路程+2.5至3.5小时的路程=24千米,求出顺流的速度,然后根据不同的x的范围,用待定系数法求出y与x的函数关系式.
(4)根据(3)求出的顺流的速度可求出水流的速度,然后根据船追救生圈的距离+救生圈顺水的距离=二者在掉落时间到追及时间拉开的距离.求出自变量的值,进而求出甲船到A港的距离.
科目:czsx 来源:2013年初中数学单元提优测试卷-反比例函数与一次函数的图像(带解析) 题型:填空题
已知正比例函数y=kx与反比例函数y= 相交于点A(1,b)、点B(c,﹣2),求k+a的值.甲同学说:未知数太多,很难求的;乙同学说:可能不是用待定系数法来求;丙说:如果用数形结合的方法,利用两交点在坐标系中位置的特殊性,可以试试.请结合他们的讨论求出k+a= .
相交于点A(1,b)、点B(c,﹣2),求k+a的值.甲同学说:未知数太多,很难求的;乙同学说:可能不是用待定系数法来求;丙说:如果用数形结合的方法,利用两交点在坐标系中位置的特殊性,可以试试.请结合他们的讨论求出k+a= .
科目:czsx 来源: 题型:填空题
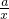 相交于点A(1,b)、点B(c,-2),求k+a的值.甲同学说:未知数太多,很难求的;乙同学说:可能不是用待定系数法来求;丙说:如果用数形结合的方法,利用两交点在坐标系中位置的特殊性,可以试试.请结合他们的讨论求出k+a=________.
相交于点A(1,b)、点B(c,-2),求k+a的值.甲同学说:未知数太多,很难求的;乙同学说:可能不是用待定系数法来求;丙说:如果用数形结合的方法,利用两交点在坐标系中位置的特殊性,可以试试.请结合他们的讨论求出k+a=________.科目:czsx 来源: 题型:
| a-1 |