练习册

  • 练习册
  • 试题
    精英家教网 > 试题搜索列表 >在下面的方格上画出函数 用单调性定义证

    在下面的方格上画出函数 用单调性定义证答案解析

    科目：gzsx 来源： 题型：

    已知函数是定义域为的奇函数，当时，．

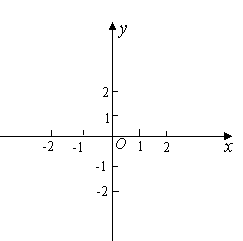    （Ⅰ）求函数的解析式；（Ⅱ）在下面的坐标系中画出函数的图象（不需列表）；

    （Ⅲ）写出函数的单调区间（不需证明）．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    （本题14分）已知

    （1）在下面方格纸上画出函数的图像

    （2）若时，求t的值。

    （3）用单调性证明函数在（1，+∞）上单调递减。

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    从某中学高二年级随机抽取60名男生身高如下（单位：cm）
    173   179   170   173   171   168   171   159   186   175
    161   165   175   177   174   162   173   178   170   172
    166   178   182   175   170   177   169   174   168   170
    180   171   165   161   178   173   170   174   170   179
    167   179   162   178   166   185   176   165   171   175
    165   170   173   157   176   178   162   176   174   175
    根据上面的数据：
    （1）选择起点为156.5，组距为5，完成下面的频率分布表；
    分组 频数 频率
    合计
    频率/组距
    （2）在下面的坐标系中画出频率分布直方图；

    （3）估计高二年级男生身高在166.5～176.5之间的比例．

    查看答案和解析>>

    科目：gzsx 来源：2008-2009学年北京市师大实验中学高二（上）期中数学试卷（理科一卷）（解析版） 题型：解答题

    从某中学高二年级随机抽取60名男生身高如下（单位：cm）
    173   179   170   173   171   168   171   159   186   175
    161   165   175   177   174   162   173   178   170   172
    166   178   182   175   170   177   169   174   168   170
    180   171   165   161   178   173   170   174   170   179
    167   179   162   178   166   185   176   165   171   175
    165   170   173   157   176   178   162   176   174   175
    根据上面的数据：
    （1）选择起点为156.5，组距为5，完成下面的频率分布表；
    分组频数频率
    合计
    频率/组距
    （2）在下面的坐标系中画出频率分布直方图；

    （3）估计高二年级男生身高在166.5～176.5之间的比例．

    查看答案和解析>>

    科目：gzsx 来源：2008-2009学年北京市师大实验中学高二（上）期中数学试卷（文科）（解析版） 题型：解答题

    从某中学高二年级随机抽取60名男生身高如下（单位：cm）
    173   179   170   173   171   168   171   159   186   175
    161   165   175   177   174   162   173   178   170   172
    166   178   182   175   170   177   169   174   168   170
    180   171   165   161   178   173   170   174   170   179
    167   179   162   178   166   185   176   165   171   175
    165   170   173   157   176   178   162   176   174   175
    根据上面的数据：
    （1）选择起点为156.5，组距为5，完成下面的频率分布表；
    分组频数频率
    合计
    频率/组距
    （2）在下面的坐标系中画出频率分布直方图；

    （3）估计高二年级男生身高在166.5～176.5之间的比例．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    设函数f（x）=|x2-4x-5|，x∈R．
    （1）在区间[-2，6]上画出函数f（x）的图象（要求列表描点）；
    （2）写出该函数在R上的单调区间；
    （3）写出函数在区间[-2，6]上的值域．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    函数y=2sin（2x+φ）（0＜φ＜
    π
    2
    ）的一条对称轴为直线x=
    π
    12
    ．
    （1）求φ；
    （2）求该函数对称中心、单调区间；
    （3）在图上画出函数y=2sin（2x+φ）在[-
    π
    6
    ，
    5π
    6
    ]上的简图．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    探究函数f（x）=2x+
    8
    x
    -3，x∈（0，+∞）上的最小值，并确定取得最小值时x的值．列表如下：
    x … 0.5 1 1.5 1.7 1.9 2 2.1 2.2 2.3 3 4 5 7 …
    y … 14 7 5.34 5.11 5.01 5 5.01 5.04 5.08 5.67 7 8.6 12.14 …
    （1）观察表中y值随x值变化趋势特点，请你直接写出函数f（x）=2x+
    8
    x
    -3，x∈（0，+∞）的单调区间，并指出当x取何值时函数的最小值为多少；
    （2）用单调性定义证明函数f（x）=2x+
    8
    x
    -3在（0，2）上的单调性．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    设函数f（x）=|x2-4x-5|．
    （1）在区间[-2，6]上画出函数f（x）的图象；
    （2）设集合A={x|f（x）≥5}，B=（-∞，-2]∪[0，4]∪[6，+∞）．试判断集合A和B之间的关系，并给出证明．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    设函数f（x）=|x2-2x|．
    （1）在区间[-1，4]上画出函数f（x）的图象；
    （2）根据图象写出该函数在[-1，4]上的单调区间；
    （3）试讨论方程f（x）=a在区间[-1，4]上实数根的情况，并加以简要说明．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    设函数f（x）=|x2-4x-5|．
    （1）在区间[-2，6]上画出函数f（x）的图象；
    （2）当k＞2时，求证：在区间[-1，5]上，y=kx+3k的图象位于函数f（x）图象的上方．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    设函数f（x）=|x2-4x-5|，g（x）=k．
    （1）在区间[-2，6]上画出函数f（x）的图象．
    （2）若函数f（x）与g（x）有3个交点，求k的值；
    （3）试分析函数ϕ（x）=|x2-4x-5|-k的零点个数．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    精英家教网设f（x）=
    x+2(x≤-1)
    x2(-1＜x＜2)
    2x(x≥2)
    ，
    （1）在如图直角坐标系中画出f（x）的图象；
    （2）若f（t）=3，求t值；
    （3）用单调性定义证明函数f（x）在[2，+∞）时单调递增．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知f(x)=loga
    x+1x-1
    （a＞0且a≠1）．
    （1）判断函数f（x）的奇偶性，并证明；
    （2）若a＞1，用单调性定义证明函数f（x）在区间（1，+∞）上单调递减；
    （3）是否存在实数a，使得f（x）的定义域为[m，n]时，值域为[1-logan，1-logam]，若存在，求出实数a的取值范围；若不存在，则说明理由．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    我们把形如f(x)=
    a|x|-b
    (a，b＞0)    因其函数图象十分像汉字“囧”，故亲切称之为囧函数．现在为了方便讨论我们令a=b=1．
    （1）在直角坐标系上画出函数y=f（x）的囧图；
    （2）讨论关于x的方程f（x）=k的解的个数．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    设函数f（x）=|x2-4x-5|，x∈R．
    （1）在区间[-2，6]上画出函数f（x）的图象；
    （2）写出该函数在R上的单调区间．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知函数f（x）=
    		2
    sin（2x-
    π
    4
    ）．
    （1）求函数f（x）的最小正周期、最小值和最大值；
    （2）在图上画出函数f（x）在区间[0，π]内的图象．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    设函数f（x）=|x2-2x|．
    （1）在区间[-2，6]上画出函数f（x）的图象；
    （2）根据图象写出该函数在[-2，6]上的单调区间；
    （3）方程f（x）=a在区间[-2，6]有两个不同的实数根，求a的取值范围．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    设函数f（x）=|x2-4x-5|．
    （1）在区间[-2，6]上画出函数f（x）的图象；
    （2）设集合A={x|f（x）≥5}，B=（-∞，-2]∪[0，4]∪[6，+∞）．试判断集合A和B之间的关系（要写出判断过程）；
    （3）当k＞2时，求证：在区间[-1，5]上，y=kx+3k的图象位于函数f（x）图象的上方．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    设函数f（x）=|x2-2x-8|．
    （1）在区间[-3，5]上画出函数f（x）的图象；
    （2）设集合A={x|f（x）≥5}，B=（-∞，-3]∪[-1，3]∪[5，+∞）．写出集合A和B之间的关系（相等或子集或真子集）；
    （3）当k＞2时，求证：在区间[-2，4]上，函数f（x）图象位于函数y=kx+4k的图象的下方．

    查看答案和解析>>