练习册

  • 练习册
  • 试题
    精英家教网 > 试题搜索列表 >已知抛物线y=x2+kx+1 与x轴两个

    已知抛物线y=x2+kx+1 与x轴两个答案解析

    科目：czsx 来源： 题型：

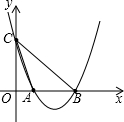    精英家教网如图，已知二次函数y=x2-4x+3的图象交x轴于A、B两点（点A在点B的左侧）抛物线y=x2-4x+3交y轴于点C．
    （1）求线段BC所在直线的解析式．
    （2）又已知反比例函数y=
    kx
    与BC有两个交点且k为正整数，求k的值．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    已知抛物线y=-x2+
    4
    		3
    3
    x与x轴交于O点和B点，与直线y=kx在第一象限交于点A（
    		3
    ，1）．
    （1）求k的值及∠AOB的度数．
    （2）现有一个半径为2的动圆，其圆心P在抛物线上运动，当⊙P恰好与y轴相切时，求P点坐标．
    （3）在抛物线上是否存在一点M，使得以M为圆心的⊙M恰好与y轴和上述直线y=kx都相切？若存在，求点M的坐标及⊙M的半径；若不存在，请说明理由．

    查看答案和解析>>

    科目：czsx 来源：2012年5月中考数学模拟试卷（1）（解析版） 题型：解答题

    已知抛物线y=-x2+x与x轴交于O点和B点，与直线y=kx在第一象限交于点A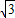（，1）．
    （1）求k的值及∠AOB的度数．
    （2）现有一个半径为2的动圆，其圆心P在抛物线上运动，当⊙P恰好与y轴相切时，求P点坐标．
    （3）在抛物线上是否存在一点M，使得以M为圆心的⊙M恰好与y轴和上述直线y=kx都相切？若存在，求点M的坐标及⊙M的半径；若不存在，请说明理由．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    已知抛物线y=x2-4x与x轴交于点A，B，顶点为C，则△ABC的面积为
     
    ．

    查看答案和解析>>

    科目：czsx 来源： 题型：

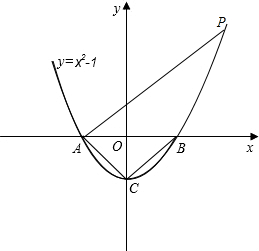    精英家教网如图，已知抛物线y=x2-1与x轴交于A、B两点，与y轴交于点C．过点A作AP∥BC交抛物线于点P．
    （1）求A、B、C三点的坐标以及直线BC的解析式；
    （2）求点P的坐标以及四边形ACBP的面积；
    （3）在抛物线上是否存在点M，过点M作MN垂直x轴于点N，使以A、M、N三点为顶点的三角形与三角形PCA相似？若存在，求出M点的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：czsx 来源： 题型：

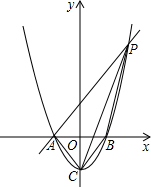    精英家教网如图所示，已知抛物线y=x2-1与x轴交于A、B两点，与y轴交于点C．过点A作AP∥CB交抛物线于点P，点M在x轴上方的抛物线上，过M作MG⊥x轴于点G，以A、M、G三点为顶点的三角形与△PCA相似．则点M的坐标为
     
    ．

    查看答案和解析>>

    科目：czsx 来源： 题型：

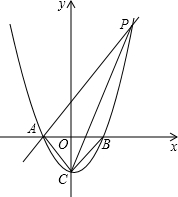    精英家教网如图所示，已知抛物线y=x2-1与x轴交于A、B两点，与y轴交于点C．
    （1）求A、B、C三点的坐标；
    （2）过点A作AP∥CB交抛物线于点P，求四边形ACBP的面积；
    （3）在x轴上方的抛物线上是否存在一点M，过M作MG⊥x轴于点G，使以A、M、G三点为顶点的三角形与△PCA相似？若存在，请求出M点的坐标；否则，请说明理由．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    已知抛物线y=x2+3x与x轴交于A、B两点，在x轴上方的抛物线上存在一点P，使△PAB的面积等于3，
    （1）求A、B两点的坐标；
    （2）求出点P的坐标．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    如图所示，已知抛物线y=x2-1与x轴交于A、B两点，与y轴交于点c．

        1.(1)求A、B、C三点的坐标．

        2.(2)过点A作AP∥CB交抛物线于点P，求四边形ACBP的面积．

      3. (3)在x轴上方的抛物线上是否存在一点M，过M作MG⊥x轴于点G，使以A、M、G三点为顶点的三角形与△PCA相似．若存在，请求出M点的坐标；否则，请说明理由。

     

    查看答案和解析>>

    科目：czsx 来源：2013-2014学年江西省九年级3月月考数学试卷（解析版） 题型：解答题

    如图，已知抛物线y=x2-1与x轴交于A、B两点，与y轴交于点C．

    （1）求A、B、C三点的坐标．

    （2）过点A作AP∥CB交抛物线于点P，求四边形ACBP的面积．

    （3）在轴上方的抛物线上是否存在一点M，过M作MG轴于点G，使以A、M、G三点为顶点的三角形与PCA相似．若存在，请求出M点的坐标；否则，请说明理由．

     

    查看答案和解析>>

    科目：czsx 来源：2012届人教版九年级第一学期期末考试数学卷 题型：选择题

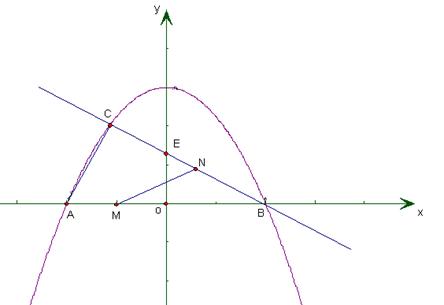
    （本题12分）如图，已知抛物线y=x2+3与x轴交于点A、B,与直线y=x+b相交于点B、C,直线y=x+b与y轴交于点E.

    （1）写出直线BC的解析式；

     (2)求△ABC的面积；

     (3)若点M在线段AB上以每秒1个单位长度的速度从A向B运动（不与A、B重合），同时，点N在射线BC上以每秒2个单位长度的速度从B向C运动。设运动时间为t秒，请写出△MNB的面积s与t的函数关系式，并求出点M运动多少时间时，△MNB的面积最大，最大面积是多少？

     

     

     

     

     

    查看答案和解析>>

    科目：czsx 来源：2009-2010学年浙江省宁波市兰江中学九年级（上）第二次段考数学试卷（解析版） 题型：填空题

    如图所示，已知抛物线y=x2-1与x轴交于A、B两点，与y轴交于点C．过点A作AP∥CB交抛物线于点P，点M在x轴上方的抛物线上，过M作MG⊥x轴于点G，以A、M、G三点为顶点的三角形与△PCA相似．则点M的坐标为    ．

    查看答案和解析>>

    科目：czsx 来源：2011-2012学年北京市154中九年级上学期期中考试数学卷 题型：解答题

    如图所示，已知抛物线y=x2-1与x轴交于A、B两点，与y轴交于点c．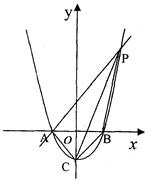

    【小题1】(1)求A、B、C三点的坐标．
    【小题2】(2)过点A作AP∥CB交抛物线于点P，求四边形ACBP的面积．
    【小题3】 (3)在x轴上方的抛物线上是否存在一点M，过M作MG⊥x轴于点G，使以A、M、G三点为顶点的三角形与△PCA相似．若存在，请求出M点的坐标；否则，请说明理由。

    查看答案和解析>>

    科目：czsx 来源：2013年浙江省湖州市中考数学模拟试卷（十四）（解析版） 题型：解答题

    如图，已知抛物线y=x2-1与x轴交于A、B两点，与y轴交于点C．过点A作AP∥BC交抛物线于点P．
    （1）求A、B、C三点的坐标以及直线BC的解析式；
    （2）求点P的坐标以及四边形ACBP的面积；
    （3）在抛物线上是否存在点M，过点M作MN垂直x轴于点N，使以A、M、N三点为顶点的三角形与三角形PCA相似？若存在，求出M点的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：czsx 来源：2011-2012年北京市九年级上学期期中考试数学卷 题型：解答题

    如图所示，已知抛物线y=x2-1与x轴交于A、B两点，与y轴交于点c．

        1.(1)求A、B、C三点的坐标．

        2.(2)过点A作AP∥CB交抛物线于点P，求四边形ACBP的面积．

       3. (3)在x轴上方的抛物线上是否存在一点M，过M作MG⊥x轴于点G，使以A、M、G三点为顶点的三角形与△PCA相似．若存在，请求出M点的坐标；否则，请说明理由。

     

    查看答案和解析>>

    科目：czsx 来源：2011年安徽省阜阳市十五中中考数学三模试卷（解析版） 题型：解答题

    如图，已知抛物线y=x2-1与x轴交于A、B两点，与y轴交于点C．过点A作AP∥BC交抛物线于点P．
    （1）求A、B、C三点的坐标以及直线BC的解析式；
    （2）求点P的坐标以及四边形ACBP的面积；
    （3）在抛物线上是否存在点M，过点M作MN垂直x轴于点N，使以A、M、N三点为顶点的三角形与三角形PCA相似？若存在，求出M点的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：czsx 来源：2011年浙江省金华市金东区中考数学一模试卷（解析版） 题型：解答题

    如图，已知抛物线y=x2-1与x轴交于A、B两点，与y轴交于点C．过点A作AP∥BC交抛物线于点P．
    （1）求A、B、C三点的坐标以及直线BC的解析式；
    （2）求点P的坐标以及四边形ACBP的面积；
    （3）在抛物线上是否存在点M，过点M作MN垂直x轴于点N，使以A、M、N三点为顶点的三角形与三角形PCA相似？若存在，求出M点的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：czsx 来源： 题型：解答题

    如图，已知抛物线y=x2-1与x轴交于A、B两点，与y轴交于点C．过点A作AP∥BC交抛物线于点P．
    （1）求A、B、C三点的坐标以及直线BC的解析式；
    （2）求点P的坐标以及四边形ACBP的面积；
    （3）在抛物线上是否存在点M，过点M作MN垂直x轴于点N，使以A、M、N三点为顶点的三角形与三角形PCA相似？若存在，求出M点的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：czsx 来源：2011-2012学年人教版九年级第一学期期末考试数学卷 题型：解答题

    （本题12分）如图，已知抛物线y=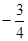x2+3与x轴交于点A、B,与直线y=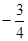x+b相交于点B、C,直线y=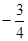x+b与y轴交于点E.
    （1）写出直线BC的解析式；
    (2)求△ABC的面积；
    (3)若点M在线段AB上以每秒1个单位长度的速度从A向B运动（不与A、B重合），同时，点N在射线BC上以每秒2个单位长度的速度从B向C运动。设运动时间为t秒，请写出△MNB的面积s与t的函数关系式，并求出点M运动多少时间时，△MNB的面积最大，最大面积是多少？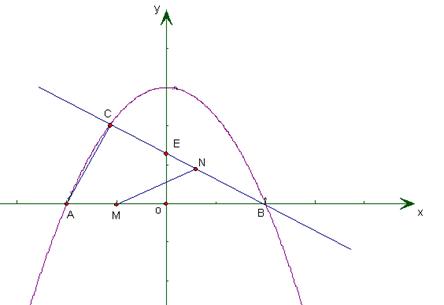

    查看答案和解析>>

    科目：czsx 来源： 题型：

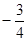    （本题12分）如图，已知抛物线y=x2+3与x轴交于点A、B,与直线y=x+b相交于点B、C,直线y=x+b与y轴交于点E.

    （1）写出直线BC的解析式；

     (2)求△ABC的面积；

     (3)若点M在线段AB上以每秒1个单位长度的速度从A向B运动（不与A、B重合），同时，点N在射线BC上以每秒2个单位长度的速度从B向C运动。设运动时间为t秒，请写出△MNB的面积s与t的函数关系式，并求出点M运动多少时间时，△MNB的面积最大，最大面积是多少？

     

     

     

     

     

    查看答案和解析>>