如图，已知AC垂直于BD与C，BC=CE,AC=DC.求证：AB=DE答案解析
科目：czsx
来源：
题型：
如图，已知OE垂直于直线AB，垂足为点O，射线OD在北偏东35°的方向，反向延长射线OD于点C．
（1）∠DOE=
35°
35°
；
（2）求∠AOC的度数．
查看答案和解析>>
科目：czsx
来源：
题型：
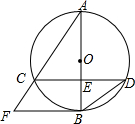
如图，已知⊙O的直径AB与弦CD互相垂直，垂足为点E．⊙O的切线BF与弦AC的延长线相交于点F，且AC=8，tan∠BDC=
．
（1）求⊙O的半径长；
（2）求线段CF长．
查看答案和解析>>
科目：czsx
来源：
题型：
如图，已知在四边形ABFC中∠ACB=90°，BC的垂直平分线EF交BC于点D，交AB于点E，且CF=AE．
（1）试探究，四边形BECF是什么特殊的四边形并证明之；
（2）若四边形BECF的面积是6cm
2且BC+AC=
cm时．求AB．
查看答案和解析>>
科目：czsx
来源：
题型：
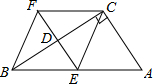
如图，已知在四边形ABFC中∠ACB=90°，BC的垂直平分线EF交BC于点D，交AB于点E，且CF=AE．
（1）试探究，四边形BECF是什么特殊的四边形并证明之；
（2）当∠A的大小满足什么条件时四边形BECF是正方形？并证明你的结论．
（3）若四边形BECF的面积是6（cm）
2且BC+AC=
cm时，求AB．
查看答案和解析>>
科目：czsx
来源：
题型：
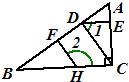
19、如图，已知AC⊥BC，CD⊥AB，DE⊥AC，∠1+∠2=180°，要证HF⊥AB，请完善证明过程，并在括号内填上相应依据：
∵AC⊥BC，DE⊥AC，（已知）
∴DE∥BC （在同一平面内，垂直于同一条直线的两条直线平行）
∴∠
1
=∠
DCB
（
两直线平行，内错角相等
）
∵∠1+∠2=180° （已知）
∴∠
DCB
+∠
2
=180°
∴
CD
∥
FH
（
同旁内角互补，两直线平行
）
∵CD⊥AB（已知）
∴∠CDB=∠HFB=90° （
两直线平行，同位角相等
）
∴HF⊥AB
查看答案和解析>>
科目：czsx
来源：
题型：
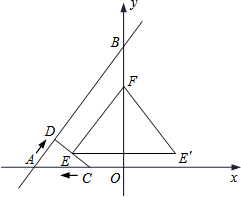
如图，已知直线y=
x+4与x轴、y轴分别相交于点A、B，点C从O点出发沿射线OA以每秒1个单位长度的速度匀速运动，同时点D从A点出发沿AB以每秒1个单位长度的速度向B点匀速运动，当点D到达B点时C、D都停止运动．点E是CD的中点，直线EF⊥CD交y轴于点F，点E′与E点关于y轴对称．点C、D的运动时间为t（秒）．
（1）当t=1时，AC=
2
2
，点D的坐标为
；
（2）设四边形BDCO的面积为S，当0＜t＜3时，求S与t的函数关系式；
（3）当直线EF与△AOB的一边垂直时，求t的值；
（4）当△EFE′为等腰直角三角形时，直接写出t的值．
查看答案和解析>>
科目：czsx
来源：
题型：
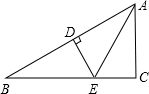
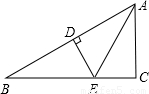
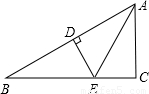
如图，已知DE垂直平分AB，分别交AB、BC于D、E两点，AE平分∠BAC，∠B=30°，BE=4，求AC的长．
查看答案和解析>>
科目：czsx
来源：
题型：
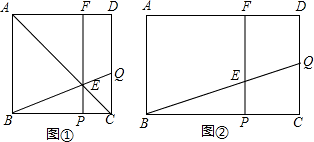
如图，已知矩形ABCD中，AB=4cm，BC=a厘米（a＞4）．动点P、Q同时从C点出发，点P在线段CB上以1厘米/秒的速度由C点向B点运动，点Q在线段CD上以相同的速度由C点向D点运动，过点P作直线垂直于BC，分别交BQ、AD于点E、F，当点Q到达终点D时，点P随之停止运动．设运动时间为t秒（t＞0）．
（1）如图①，若a=5厘米，在运动过程中，当点E在矩形ABCD的对角线AC上时，求t的值；
（2）如图②，若a=6厘米，在运动过程中，是否存在某一时刻t，使得∠BFQ=90°？若存在，请求出此时t的值；若不存在，请说明理由；
（3）若经过t秒后，恰好使矩形ABPF的面积与直角三角形BCQ的面积相等，求a的取值范围．
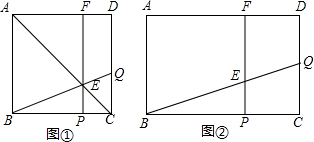
查看答案和解析>>
科目：czsx
来源：2005年湖南省岳阳市中考数学试卷（课标卷）（解析版）
题型：解答题
（2005•岳阳）如图，已知DE垂直平分AB，分别交AB、BC于D、E两点，AE平分∠BAC，∠B=30°，BE=4，求AC的长．
查看答案和解析>>
科目：czsx
来源：
题型：解答题
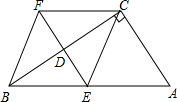如图，已知在四边形ABFC中∠ACB=90°，BC的垂直平分线EF交BC于点D，交AB于点E，且CF=AE．
（1）试探究，四边形BECF是什么特殊的四边形并证明之；
（2）若四边形BECF的面积是6cm2且BC+AC=
cm时．求AB．
查看答案和解析>>
科目：czsx
来源：岳阳
题型：解答题
如图，已知DE垂直平分AB，分别交AB、BC于D、E两点，AE平分∠BAC，∠B=30°，BE=4，求AC的长．
查看答案和解析>>
科目：czsx
来源：上海期末题
题型：解答题
如图，已知 AC垂直平分BD于点O。
（1）图中有多少对全等三角形？请把它们都写出来；
（2）任选（1）中的一对全等三角形加以证明。
查看答案和解析>>
科目：czsx
来源：
题型：解答题
如图，已知矩形ABCD中，AB=4cm，BC=a厘米（a＞4）．动点P、Q同时从C点出发，点P在线段CB上以1厘米/秒的速度由C点向B点运动，点Q在线段CD上以相同的速度由C点向D点运动，过点P作直线垂直于BC，分别交BQ、AD于点E、F，当点Q到达终点D时，点P随之停止运动．设运动时间为t秒（t＞0）．
（1）如图①，若a=5厘米，在运动过程中，当点E在矩形ABCD的对角线AC上时，求t的值；
（2）如图②，若a=6厘米，在运动过程中，是否存在某一时刻t，使得∠BFQ=90°？若存在，请求出此时t的值；若不存在，请说明理由；
（3）若经过t秒后，恰好使矩形ABPF的面积与直角三角形BCQ的面积相等，求a的取值范围．
查看答案和解析>>
科目：czsx
来源：
题型：解答题
如图，已知⊙O的直径AB与弦CD互相垂直，垂足为点E．⊙O的切线BF与弦AC的延长线相交于点F，且AC=8，tan∠BDC=
．
（1）求⊙O的半径长；
（2）求线段CF长．
查看答案和解析>>
科目：czsx
来源：
题型：填空题
如图，已知AC⊥BC，CD⊥AB，DE⊥AC，∠1+∠2=180°，要证HF⊥AB，请完善证明过程，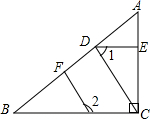
并在括号内填上相应依据：
∵AC⊥BC，DE⊥AC，（已知）
∴DE∥BC （在同一平面内，垂直于同一条直线的两条直线平行）
∴∠________=∠________（________）
∵∠1+∠2=180° （已知）
∴∠________+∠________=180°
∴________∥________（________）
∵CD⊥AB（已知）
∴∠CDB=∠HFB=90° （________）
∴HF⊥AB．
查看答案和解析>>
科目：czsx
来源：2005年全国中考数学试题汇编《三角形》（10）（解析版）
题型：解答题
（2005•岳阳）如图，已知DE垂直平分AB，分别交AB、BC于D、E两点，AE平分∠BAC，∠B=30°，BE=4，求AC的长．
查看答案和解析>>
科目：czsx
来源：
题型：解答题
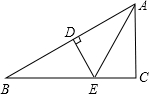如图，已知DE垂直平分AB，分别交AB、BC于D、E两点，AE平分∠BAC，∠B=30°，BE=4，求AC的长．
查看答案和解析>>
科目：czsx
来源：2010年内蒙古包头市中考数学试卷（解析版）
题型：解答题
如图，已知矩形ABCD中，AB=4cm，BC=a厘米（a＞4）．动点P、Q同时从C点出发，点P在线段CB上以1厘米/秒的速度由C点向B点运动，点Q在线段CD上以相同的速度由C点向D点运动，过点P作直线垂直于BC，分别交BQ、AD于点E、F，当点Q到达终点D时，点P随之停止运动．设运动时间为t秒（t＞0）．
（1）如图①，若a=5厘米，在运动过程中，当点E在矩形ABCD的对角线AC上时，求t的值；
（2）如图②，若a=6厘米，在运动过程中，是否存在某一时刻t，使得∠BFQ=90°？若存在，请求出此时t的值；若不存在，请说明理由；
（3）若经过t秒后，恰好使矩形ABPF的面积与直角三角形BCQ的面积相等，求a的取值范围．
查看答案和解析>>
科目：czsx
来源：四川省期中题
题型：解答题
如图，已知在四边形ABFC中∠ACB=90°，BC的垂直平分线EF交BC于点D，交AB于点E，且CF=AE．
（1）试探究，四边形BECF是什么特殊的四边形并证明之；
（2）若四边形BECF的面积是6cm
2且BC+AC=
cm时．求AB．
查看答案和解析>>
科目：czsx
来源：专项题
题型：填空题
如图，已知DE垂直平分AB，分别交AB、BC于D、E两点，AE平分∠BAC，∠B=30°，BE=4，则AC= _________ 。
查看答案和解析>>
