在矩形ABCD的一边AD=8,他的对角线AC=10CM,BE⊥AC于点E答案解析
科目:czsx
来源:上海市松江区2011届中考二模数学试题
题型:022
在矩形ABCD中,AD=4,对角线AC、BD交于点O,P为AB的中点,将△ADP绕点A顺时针旋转,使点D恰好落在点O处,点P落在点P/处,那么点P/与点B的距离为________.
查看答案和解析>>
科目:czsx
来源:
题型:

20、如图,在四边形ABCD中,AD<BC,对角线AC、BD相交于O点,AC=BD,∠ACB=∠DBC.
(1)求证:四边形ABCD为等腰梯形.
(2)若E为AB上一点,延长DC至F,使CF=BE,连接EF交BC于G,请判断G点是否为EF中点,并说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
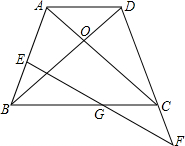 如图,在四边形ABCD中,AD<BC,对角线AC、BD相交于O点,AC=BD,∠ACB=∠DBC.
如图,在四边形ABCD中,AD<BC,对角线AC、BD相交于O点,AC=BD,∠ACB=∠DBC.
(1)求证:四边形ABCD为等腰梯形.
(2)若E为AB上一点,延长DC至F,使CF=BE,连接EF交BC于G,请判断G点是否为EF中点,并说明理由.
查看答案和解析>>
科目:czsx
来源:2010年四川省成都市双流县中考数学试卷(解析版)
题型:解答题
如图,在四边形ABCD中,AD<BC,对角线AC、BD相交于O点,AC=BD,∠ACB=∠DBC.
(1)求证:四边形ABCD为等腰梯形.
(2)若E为AB上一点,延长DC至F,使CF=BE,连接EF交BC于G,请判断G点是否为EF中点,并说明理由.

查看答案和解析>>
科目:czsx
来源:双流县
题型:解答题
如图,在四边形ABCD中,AD<BC,对角线AC、BD相交于O点,AC=BD,∠ACB=∠DBC.
(1)求证:四边形ABCD为等腰梯形.
(2)若E为AB上一点,延长DC至F,使CF=BE,连接EF交BC于G,请判断G点是否为EF中点,并说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
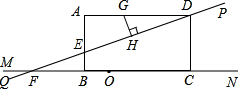
如图,在矩形ABCD中,AD=8,点E是AB边上的一点,AE=2
.过D,E两点作直线PQ,与BC边所在的直线MN相交于点F.
(1)求tan∠ADE的值;
(2)点G是线段AD上的一个动点,GH⊥DE,垂足为H.设DG为x,四边形AEHG的面积为y,试写出y与x之间的函数关系式;
(3)如果AE=2EB,点O是直线MN上的一个动点,以O为圆心作圆,使⊙O与直线PQ相切,同时又与矩形ABCD的某一边相切.问满足条件的⊙O有几个?并求出其中一个圆的半径.
查看答案和解析>>
科目:czsx
来源:
题型:
(2012•江宁区二模)数学实验室:小明取出一张矩形纸片ABCD,AD=BC=5,AB=CD=25.他先在矩形ABCD的边AB上取一点M,接着在CD上取一点N,然后将纸片沿MN折叠,使MB′与DN交于点K,得到△MNK(如图①).
(1)试判断△MNK的形状,并说明理由.
(2)如何折叠能够使△MNK的面积最大?请你利用备用图探究可能出现的情况,求出最大值.

查看答案和解析>>
科目:czsx
来源:
题型:阅读理解
阅读下列材料:
小贝遇到一个有趣的问题:在矩形ABCD中,AD=8cm,AB=6cm.现有一动点P按下列方式在矩形内运动:它从A点出发,沿着AB边夹角为45°的方向作直线运动,每次碰到矩形的一边,就会改变运动方向,沿着与这条边夹角为45°的方向作直线运动,并且它一直按照这种方式不停地运动,即当P点碰到BC边,沿着BC边夹角为45°的方向作直线运动,当P点碰到CD边,再沿着与CD边夹角为45°的方向作直线运动,…,如图1所示,
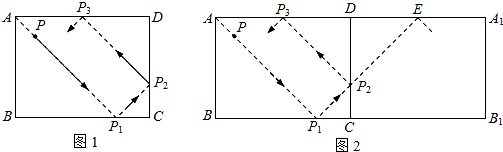
问P点第一次与D点重合前与边相碰几次,P点第一次与D点重合时所经过的路径的总长是多少.小贝的思考是这样开始的:如图2,将矩形ABCD沿直线CD折叠,得到矩形A
1B
1CD,由轴对称的知识,发现P
2P
3=P
2E,P
1A=P
1E.
请你参考小贝的思路解决下列问题:
(1)P点第一次与D点重合前与边相碰
次;P点从A点出发到第一次与D点重合时所经过的路径的总长是
cm;
(2)近一步探究:改变矩形ABCD中AD、AB的长,且满足AD>AB,动点P从A点出发,按照阅读材料中动点的运动方式,并满足前后连续两次与边相碰的位置在矩形ABCD相邻的两边上.若P点第一次与B点重合前与边相碰7次,则AB:AD的值为
.
查看答案和解析>>
科目:czsx
来源:
题型:
(2012•南京)下框中是小明对一道题目的解答以及老师的批改.
题目:某村计划建造如图所示的矩形蔬菜温室,要求长与宽的比为2:1,在温室内,沿前侧内墙保留3m的空地,其他三侧内墙各保留1m的通道,当温室的长与宽各为多少时,矩形蔬菜种植区域的面积是288m2?
解:设矩形蔬菜种植区域的宽为xm,则长为2xm,
根据题意,得x•2x=288.
解这个方程,得x1=-12(不合题意,舍去),x2=12
所以温室的长为2×12+3+1=28(m),宽为12+1+1=14(m)
答:当温室的长为28m,宽为14m时,矩形蔬菜种植区域的面积是288m2.我的结果也正确!
小明发现他解答的结果是正确的,但是老师却在他的解答中画了一条横线,并打了一个?.
结果为何正确呢?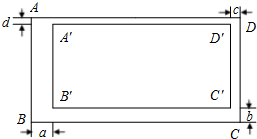
(1)请指出小明解答中存在的问题,并补充缺少的过程:
变化一下会怎样…
(2)如图,矩形A′B′C′D′在矩形ABCD的内部,AB∥A′B′,AD∥A′D′,且AD:AB=2:1,设AB与A′B′、BC与B′C′、CD与C′D′、DA与D′A′之间的距离分别为a、b、c、d,要使矩形A′B′C′D′∽矩形ABCD,a、b、c、d应满足什么条件?请说明理由.
查看答案和解析>>
科目:czsx
来源:2012年初中毕业升学考试(江苏南京卷)数学(带解析)
题型:解答题
“?”的思考

下框中是小明对一道题目的解答以及老师的批阅。
我的结果也正确 小明发现他解答的结果是正确的,但是老师却在他的解答中划了一条横线,并打开了一个“?” 结果为何正确呢? (1)请指出小明解答中存在的问题,并补充缺少的过程: 变化一下会怎样…… (2)如图,矩形A′B′C′D′在矩形ABCD的内部,AB∥A′B′,AD∥A′D′,且AD:AB=2:1,设AB与A′B′、BC与B′C′、CD与C′D′、DA与D′A′之间的距离分别为a、b、c、d,要使矩形A′B′C′D′∽矩形ABCD,a、b、c、d应满足什么条件?请说明理由. 
查看答案和解析>>
科目:czsx
来源:2012届江苏省南京市江宁区九年级中考二模数学试卷(带解析)
题型:解答题
数学实验室:小明取出一张矩形纸片ABCD,AD=BC=5,AB=CD=25.他先在矩形ABCD的边AB上取一点M,接着在CD上取一点N,然后将纸片沿MN折叠,使MB′与DN交于点K,得到△MNK(如图①).
(1)试判断△MNK的形状,并说明理由.

(2)如何折叠能够使△MNK的面积最大?请你利用备用图探究可能出现的情况,求出最大值.
查看答案和解析>>
科目:czsx
来源:2011-2012学年江苏省南京市江宁区九年级中考二模数学试卷(解析版)
题型:解答题
数学实验室:小明取出一张矩形纸片ABCD,AD=BC=5,AB=CD=25.他先在矩形ABCD的边AB上取一点M,接着在CD上取一点N,然后将纸片沿MN折叠,使MB′与DN交于点K,得到△MNK(如图①).
(1)试判断△MNK的形状,并说明理由.

(2)如何折叠能够使△MNK的面积最大?请你利用备用图探究可能出现的情况,求出最大值.

查看答案和解析>>
科目:czsx
来源:2012年初中毕业升学考试(江苏南京卷)数学(解析版)
题型:解答题
“?”的思考
下框中是小明对一道题目的解答以及老师的批阅。

我的结果也正确
小明发现他解答的结果是正确的,但是老师却在他的解答中划了一条横线,并打开了一个“?”
结果为何正确呢?
(1)请指出小明解答中存在的问题,并补充缺少的过程:
变化一下会怎样……
(2)如图,矩形A′B′C′D′在矩形ABCD的内部,AB∥A′B′,AD∥A′D′,且AD:AB=2:1,设AB与A′B′、BC与B′C′、CD与C′D′、DA与D′A′之间的距离分别为a、b、c、d,要使矩形A′B′C′D′∽矩形ABCD,a、b、c、d应满足什么条件?请说明理由.

查看答案和解析>>
科目:czsx
来源:2005年全国中考数学试题汇编《圆》(14)(解析版)
题型:解答题
(2005•金华)如图,在矩形ABCD中,AD=8,点E是AB边上的一点,AE=2 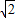 .过D,E两点作直线PQ,与BC边所在的直线MN相交于点F. (1)求tan∠ADE的值; (2)点G是线段AD上的一个动点,GH⊥DE,垂足为H.设DG为x,四边形AEHG的面积为y,试写出y与x之间的函数关系式; (3)如果AE=2EB,点O是直线MN上的一个动点,以O为圆心作圆,使⊙O与直线PQ相切,同时又与矩形ABCD的某一边相切.问满足条件的⊙O有几个?并求出其中一个圆的半径. 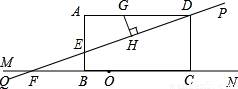
查看答案和解析>>
科目:czsx
来源:
题型:解答题
如图,在矩形ABCD中,AD=8,点E是AB边上的一点,AE=2 .过D,E两点作直线PQ,与BC边所在的直线MN相交于点F. .过D,E两点作直线PQ,与BC边所在的直线MN相交于点F.
(1)求tan∠ADE的值;
(2)点G是线段AD上的一个动点,GH⊥DE,垂足为H.设DG为x,四边形AEHG的面积为y,试写出y与x之间的函数关系式;
(3)如果AE=2EB,点O是直线MN上的一个动点,以O为圆心作圆,使⊙O与直线PQ相切,同时又与矩形ABCD的某一边相切.问满足条件的⊙O有几个?并求出其中一个圆的半径.

查看答案和解析>>
科目:czsx
来源:第35章《圆(二)》中考题集(04):35.2 直线与圆的位置关系(解析版)
题型:解答题
如图,在矩形ABCD中,AD=8,点E是AB边上的一点,AE=2  .过D,E两点作直线PQ,与BC边所在的直线MN相交于点F. (1)求tan∠ADE的值; (2)点G是线段AD上的一个动点,GH⊥DE,垂足为H.设DG为x,四边形AEHG的面积为y,试写出y与x之间的函数关系式; (3)如果AE=2EB,点O是直线MN上的一个动点,以O为圆心作圆,使⊙O与直线PQ相切,同时又与矩形ABCD的某一边相切.问满足条件的⊙O有几个?并求出其中一个圆的半径. 
查看答案和解析>>
科目:czsx
来源:2012年江苏省南京市中考数学试卷(解析版)
题型:解答题
下框中是小明对一道题目的解答以及老师的批改. 题目:某村计划建造如图所示的矩形蔬菜温室,要求长与宽的比为2:1,在温室内,沿前侧内墙保留3m的空地,其他三侧内墙各保留1m的通道,当温室的长与宽各为多少时,矩形蔬菜种植区域的面积是288m 2? 解:设矩形蔬菜种植区域的宽为xm,则长为2xm, 根据题意,得x•2x=288. 解这个方程,得x 1=-12(不合题意,舍去),x 2=12 所以温室的长为2×12+3+1=28(m),宽为12+1+1=14(m) 答:当温室的长为28m,宽为14m时,矩形蔬菜种植区域的面积是288m 2. 我的结果也正确! 小明发现他解答的结果是正确的,但是老师却在他的解答中画了一条横线,并打了一个?. 结果为何正确呢? (1)请指出小明解答中存在的问题,并补充缺少的过程: 变化一下会怎样… (2)如图,矩形A′B′C′D′在矩形ABCD的内部,AB∥A′B′,AD∥A′D′,且AD:AB=2:1,设AB与A′B′、BC与B′C′、CD与C′D′、DA与D′A′之间的距离分别为a、b、c、d,要使矩形A′B′C′D′∽矩形ABCD,a、b、c、d应满足什么条件?请说明理由. 
查看答案和解析>>
科目:czsx
来源:2005年全国中考数学试题汇编《锐角三角函数》(05)(解析版)
题型:解答题
(2005•金华)如图,在矩形ABCD中,AD=8,点E是AB边上的一点,AE=2  .过D,E两点作直线PQ,与BC边所在的直线MN相交于点F. (1)求tan∠ADE的值; (2)点G是线段AD上的一个动点,GH⊥DE,垂足为H.设DG为x,四边形AEHG的面积为y,试写出y与x之间的函数关系式; (3)如果AE=2EB,点O是直线MN上的一个动点,以O为圆心作圆,使⊙O与直线PQ相切,同时又与矩形ABCD的某一边相切.问满足条件的⊙O有几个?并求出其中一个圆的半径. 
查看答案和解析>>
科目:czsx
来源:2012年江苏省南京市江宁区中考数学二模试卷(解析版)
题型:解答题
数学实验室:小明取出一张矩形纸片ABCD,AD=BC=5,AB=CD=25.他先在矩形ABCD的边AB上取一点M,接着在CD上取一点N,然后将纸片沿MN折叠,使MB′与DN交于点K,得到△MNK(如图①). (1)试判断△MNK的形状,并说明理由. (2)如何折叠能够使△MNK的面积最大?请你利用备用图探究可能出现的情况,求出最大值. 
查看答案和解析>>
科目:czsx
来源:第7章《锐角三角函数》中考题集(25):7.5 解直角三角形(解析版)
题型:解答题
如图,在矩形ABCD中,AD=8,点E是AB边上的一点,AE=2  .过D,E两点作直线PQ,与BC边所在的直线MN相交于点F. (1)求tan∠ADE的值; (2)点G是线段AD上的一个动点,GH⊥DE,垂足为H.设DG为x,四边形AEHG的面积为y,试写出y与x之间的函数关系式; (3)如果AE=2EB,点O是直线MN上的一个动点,以O为圆心作圆,使⊙O与直线PQ相切,同时又与矩形ABCD的某一边相切.问满足条件的⊙O有几个?并求出其中一个圆的半径. 
查看答案和解析>>
|

 20、如图,在四边形ABCD中,AD<BC,对角线AC、BD相交于O点,AC=BD,∠ACB=∠DBC.
20、如图,在四边形ABCD中,AD<BC,对角线AC、BD相交于O点,AC=BD,∠ACB=∠DBC. 如图,在四边形ABCD中,AD<BC,对角线AC、BD相交于O点,AC=BD,∠ACB=∠DBC.
如图,在四边形ABCD中,AD<BC,对角线AC、BD相交于O点,AC=BD,∠ACB=∠DBC.








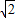 .过D,E两点作直线PQ,与BC边所在的直线MN相交于点F.
.过D,E两点作直线PQ,与BC边所在的直线MN相交于点F.