练习册

  • 练习册
  • 试题
    精英家教网 > 试题搜索列表 >菱形ABCD的边长为6，角BAD=60°，M是BC上一点，DM=2，E、F分别从A、C出发以每秒钟3:7

    菱形ABCD的边长为6，角BAD=60°，M是BC上一点，DM=2，E、F分别从A、C出发以每秒钟3:7答案解析

    科目：czsx 来源： 题型：

    已知菱形ABCD的边长为4cm，且∠ABC=60°，E是BC的中点，P在BD上，则PE+PC的最小值为
    2
    		3
    2
    		3
    ．

    查看答案和解析>>

    科目：czsx 来源： 题型：填空题

    已知菱形ABCD的边长为4cm，且∠ABC=60°，E是BC的中点，P在BD上，则PE+PC的最小值为________．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    25、菱形ABCD的边长为24厘米，∠A=60°，质点P从点A出发沿着AB-BD-DA作匀速运动，质点Q从点D同时出发沿着线路DC-CB-BD作匀速运动．
    （1）求BD的长；
    （2）已知质点P、Q运动的速度分别为4cm/秒、5cm/秒，经过12秒后，P、Q分别到达M、N两点，若按角的大小进行分类，请问△AMN是哪一类三角形，并说明理由．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    如图，菱形ABCD的边长为24厘米，∠A=60°，点P从点A出发沿线路AB→BD作匀速运动，点Q从精英家教网点D同时出发沿线路DC→CB→BA作匀速运动．
    （1）求BD的长；
    （2）已知点P、Q运动的速度分别为4厘米/秒，5厘米/秒，经过12秒后，P、Q分别到达M、N两点，若按角的大小进行分类，请你确定△AMN是哪一类三角形，并说明理由；
    （3）设（2）中的点P、Q分别从M、N同时沿原路返回，点P的速度不变，点Q的速度改变为a厘米/秒，经过3秒后，P、Q分别到达E、F两点，若△BEF与（2）中的△AMN相似，试求a的值．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    已知菱形ABCD的边长为1．∠EAF=∠ADC=60°，∠EAF的两边分别交边DC、CB于点E、F．当∠EAF绕点A旋转时，点E、F始终分别在边DC、CB上移动．
    （1）特殊发现：如图1，若点E、F分别是边DC、CB的中点．求证：菱形ABCD对角线AC、BD交点O即为△AEF的外心；
    （2）记△AEF的外心为点P．
    ①如图2．求证：△AEF为等边三角形；
    ②猜想验证：如图2．猜想△AEF的外心P落在哪一直线上，并加以证明；
    （3）拓展运用：如图3，当△AEF面积最小时，过点P任作一直线分别交边DA于点M，交边DC的延长线于点N，当MN⊥AD于M时，
    1
    DM
    +
    1
    DN
    的值为
    2
    2
    ．

    查看答案和解析>>

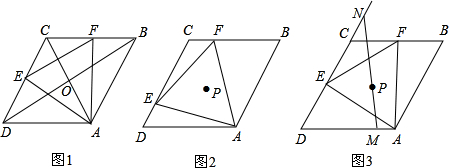
    科目：czsx 来源：2012-2013学年江苏省常州市七八年级上学期12月考数学试卷（解析版） 题型：填空题

    如图，菱形ABCD的边长为6，∠DAB=600，点P是对角线AC上一动点，Q是AB的中点，则BP+PQ的最小值是           。

     

    查看答案和解析>>

    科目：czsx 来源：2012年初中毕业升学考试（浙江湖州卷）数学（解析版） 题型：解答题

    如图1，已知菱形ABCD的边长为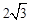，点A在x轴负半轴上，点B在坐标原点．点D的坐标为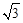（- ，3），抛物线y=ax2+b（a≠0）经过AB、CD两边的中点．

    （1）求这条抛物线的函数解析式；

    （2）将菱形ABCD以每秒1个单位长度的速度沿x轴正方向匀速平移（如图2），过点B作BE⊥CD于点E，交抛物线于点F，连接DF、AF．设菱形ABCD平移的时间为t秒（0＜t＜ 3 ）

    ①是否存在这样的t，使△ADF与△DEF相似？若存在，求出t的值；若不存在，请说明理由；

    ②连接FC，以点F为旋转中心，将△FEC按顺时针方向旋转180°，得△FE′C′，当△FE′C′落在x轴与抛物线在x轴上方的部分围成的图形中（包括边界）时，求t的取值范围．（写出答案即可）

     

    查看答案和解析>>

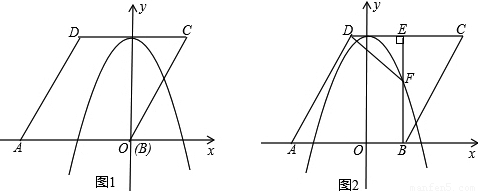
    科目：czsx 来源： 题型：

    如图1，已知菱形ABCD的边长为，点A在x轴负半轴上，点B在坐标原点．点D的坐标为（- ，3），抛物线y=ax2+b（a≠0）经过AB、CD两边的中点．

    （1）求这条抛物线的函数解析式；

    （2）将菱形ABCD以每秒1个单位长度的速度沿x轴正方向匀速平移（如图2），过点B作BE⊥CD于点E，交抛物线于点F，连接DF、AF．设菱形ABCD平移的时间为t秒（0＜t＜ 3 ）

    ①是否存在这样的t，使△ADF与△DEF相似？若存在，求出t的值；若不存在，请说明理由；

    ②连接FC，以点F为旋转中心，将△FEC按顺时针方向旋转180°，得△FE′C′，当△FE′C′落在x轴与抛物线在x轴上方的部分围成的图形中（包括边界）时，求t的取值范围．（写出答案即可）

    查看答案和解析>>

    科目：czsx 来源：2012年初中毕业升学考试（浙江湖州卷）数学（带解析） 题型：解答题

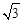    如图1，已知菱形ABCD的边长为，点A在x轴负半轴上，点B在坐标原点．点D的坐标为（- ，3），抛物线y=ax2+b（a≠0）经过AB、CD两边的中点．
    （1）求这条抛物线的函数解析式；
    （2）将菱形ABCD以每秒1个单位长度的速度沿x轴正方向匀速平移（如图2），过点B作BE⊥CD于点E，交抛物线于点F，连接DF、AF．设菱形ABCD平移的时间为t秒（0＜t＜ 3 ）
    ①是否存在这样的t，使△ADF与△DEF相似？若存在，求出t的值；若不存在，请说明理由；
    ②连接FC，以点F为旋转中心，将△FEC按顺时针方向旋转180°，得△FE′C′，当△FE′C′落在x轴与抛物线在x轴上方的部分围成的图形中（包括边界）时，求t的取值范围．（写出答案即可）

    查看答案和解析>>

    科目：czsx 来源：2010-2011学年苏科版九年级（上）国庆假日新视野（二）（解析版） 题型：解答题

    菱形ABCD的边长为24厘米，∠A=60°，质点P从点A出发沿着AB-BD-DA作匀速运动，质点Q从点D同时出发沿着线路DC-CB-BD作匀速运动．
    （1）求BD的长；
    （2）已知质点P、Q运动的速度分别为4cm/秒、5cm/秒，经过12秒后，P、Q分别到达M、N两点，若按角的大小进行分类，请问△AMN是哪一类三角形，并说明理由．

    查看答案和解析>>

    科目：czsx 来源：2011-2012学年湖北省武汉市三阳路中学九年级（下）第一次月考数学试卷（解析版） 题型：解答题

    如图，菱形ABCD的边长为24厘米，∠A=60°，点P从点A出发沿线路AB→BD作匀速运动，点Q从点D同时出发沿线路DC→CB→BA作匀速运动．
    （1）求BD的长；
    （2）已知点P、Q运动的速度分别为4厘米/秒，5厘米/秒，经过12秒后，P、Q分别到达M、N两点，若按角的大小进行分类，请你确定△AMN是哪一类三角形，并说明理由；
    （3）设（2）中的点P、Q分别从M、N同时沿原路返回，点P的速度不变，点Q的速度改变为a厘米/秒，经过3秒后，P、Q分别到达E、F两点，若△BEF与（2）中的△AMN相似，试求a的值．

    查看答案和解析>>

    科目：czsx 来源：101网校同步练习　初三数学　北师大(新课标2001/3年初审) 北师大版 题型：022

    已知菱形ABCD的边长为6，∠A＝60°，如果点P是菱形内一点，且PB＝PD＝，那么AP的长为________．

    查看答案和解析>>

    科目：czsx 来源：2011-2012学年湖北省武汉市江岸区九年级（上）期中数学试卷（解析版） 题型：解答题

    已知菱形ABCD的边长为1．∠EAF=∠ADC=60°，∠EAF的两边分别交边DC、CB于点E、F．当∠EAF绕点A旋转时，点E、F始终分别在边DC、CB上移动．
    （1）特殊发现：如图1，若点E、F分别是边DC、CB的中点．求证：菱形ABCD对角线AC、BD交点O即为△AEF的外心；
    （2）记△AEF的外心为点P．
    ①如图2．求证：△AEF为等边三角形；
    ②猜想验证：如图2．猜想△AEF的外心P落在哪一直线上，并加以证明；
    （3）拓展运用：如图3，当△AEF面积最小时，过点P任作一直线分别交边DA于点M，交边DC的延长线于点N，当MN⊥AD于M时，的值为______．

    查看答案和解析>>

    科目：czsx 来源：2011-2012学年江苏省连云港市灌云县初级中学九年级（上）段考数学试卷（解析版） 题型：填空题

    如图，菱形ABCD的边长为2，∠BCD=120°，E是AD中点，当点P在对角线BD上移动时，△PAE周长的最小值为    ．

    查看答案和解析>>

    科目：czsx 来源：2011-2012学年陕西省渭南市富平县蓝光中学九年级（上）期中数学试卷（解析版） 题型：填空题

    如图，菱形ABCD的边长为2，∠BCD=120°，E是AD中点，当点P在对角线BD上移动时，△PAE周长的最小值为    ．

    查看答案和解析>>

    科目：czsx 来源：2009-2010学年江苏省盐城市北蒋实验学校九年级（上）期中数学试卷（解析版） 题型：填空题

    如图，菱形ABCD的边长为2，∠BCD=120°，E是AD中点，当点P在对角线BD上移动时，△PAE周长的最小值为    ．

    查看答案和解析>>

    科目：czsx 来源：2006-2007学年湖北省天门市九年级（上）期末数学试卷（解析版） 题型：解答题

    如图，菱形ABCD的边长为24厘米，∠A=60°，点P从点A出发沿线路AB→BD作匀速运动，点Q从点D同时出发沿线路DC→CB→BA作匀速运动．
    （1）求BD的长；
    （2）已知点P、Q运动的速度分别为4厘米/秒，5厘米/秒，经过12秒后，P、Q分别到达M、N两点，若按角的大小进行分类，请你确定△AMN是哪一类三角形，并说明理由；
    （3）设（2）中的点P、Q分别从M、N同时沿原路返回，点P的速度不变，点Q的速度改变为a厘米/秒，经过3秒后，P、Q分别到达E、F两点，若△BEF与（2）中的△AMN相似，试求a的值．

    查看答案和解析>>

    科目：czsx 来源：2011年辽宁省盘锦市初中毕业升学考试数学试卷 题型：044

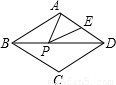
    已知菱形ABCD的边长为5，∠DAB＝60°．将菱形ABCD绕着A逆时针旋转得到菱形AEFG，设∠EAB＝α，且0°＜α＜90°，连接DG、BE、CE、CF．

    (1)如图，求证：△AGD≌△AEB；

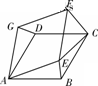
    (2)当α＝60°时，在图中画出图形并求出线段CF的长；

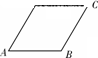
    (3)若∠CEF＝90°，在图中画出图形并求出△CEF的面积．

    查看答案和解析>>

    科目：czsx 来源：2009年吉林省初中毕业暨高中招生考试数学试卷 题型：044

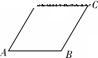
    如图所示，菱形ABCD的边长为6厘米，∠B＝60°．从初始时刻开始，点P、Q同时从A点出发，点P以1厘米/秒的速度沿A→C→B的方向运动，点Q以2厘米/秒的速度沿A→B→C→D的方向运动，当点Q运动到D点时，P、Q两点同时停止运动，设P、Q运动的时间为x秒时，△APQ与△ABC重叠部分的面积为y平方厘米(这里规定：点和线段是面积为O的三角形)，解答下列问题：

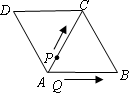
    (1)点P、Q从出发到相遇所用时间是________秒；

    (2)点P、Q从开始运动到停止的过程中，当△APQ是等边三角形时x的值是________秒；

    (3)求y与x之间的函数关系式．

    查看答案和解析>>

    科目：czsx 来源： 题型：解答题

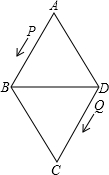    菱形ABCD的边长为24厘米，∠A=60°，质点P从点A出发沿着AB-BD-DA作匀速运动，质点Q从点D同时出发沿着线路DC-CB-BD作匀速运动．
    （1）求BD的长；
    （2）已知质点P、Q运动的速度分别为4cm/秒、5cm/秒，经过12秒后，P、Q分别到达M、N两点，若按角的大小进行分类，请问△AMN是哪一类三角形，并说明理由．

    查看答案和解析>>