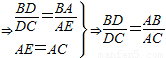成比例线段已知a-b÷a+b=1÷5,求证a+2b÷a-b=7答案解析
科目:czsx
来源:
题型:阅读理解
请阅读下面材料,并回答所提出的问题.
三角形内角平分线性质定理:三角形的内角平分线分对边所得的两条线段和这个角的两边对应成比例.
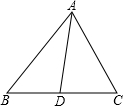
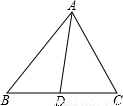
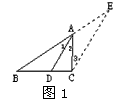
已知:如图,△ABC中,AD是角平分线.
求证:
=分析:要证
=,一般只要证BD、DC与AB、AC或BD、AB与DC、AC所在三角形相似.现在B、D、C在一直线上,△ABD与△ADC不相似,需要考虑用别的方法换比.在比例式
=中,AC恰是BD、DC、AB的第四比例项,所以考虑过C作C
E∥AD,交BA的延长线于E,从而得到BD、DC、AB的第四比例项AE,这样,证明
=就可以转化成证AE=AC.
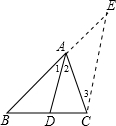
证明:过C作CE∥DA,交BA的延长线于E.
CE∥DA
⇒⇒∠E=∠3⇒AE=AC,
CE∥DA
⇒⇒=(1)上述证明过程中,用到了哪些定理?(写对两个定理即可)
(2)在上述分析、证明过程中,主要用到了下列三种数学思想的哪一种?选出一个填在后面的括号内.
[]
①数形结合思想;
②转化思想;
③分类讨论思想.
(3)用三角形内角平分线性质定理解答问题:
已知:如图,△ABC中,AD是角平分线,AB=5cm,AC=4cm,BC=7cm.求BD的长.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
三角形内角平分线性质定理:三角形的内角平分线分对边所得的两条线段和这个角的两边对应成比例。
已知:如图,△ABC中,AD是角平分线.
求证:(1)BD/DC=AB/AC
(2)若AD是三角形ABC外角的平分线,交BC延长线于点D,是否还有以上结论?
查看答案和解析>>
科目:czsx
来源:2000年全国中考数学试题汇编《图形的相似》(03)(解析版)
题型:解答题
(2000•山西)请阅读下面材料,并回答所提出的问题.
三角形内角平分线性质定理:三角形的内角平分线分对边所得的两条线段和这个角的两边对应成比例.
已知:如图,△ABC中,AD是角平分线.
求证:

分析:要证
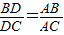
,一般只要证BD、DC与AB、AC或BD、AB与DC、AC所在三角形相似.现在B、D、C在一直线上,△ABD与△ADC不相似,需要考虑用别的方法换比.在比例式
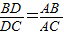
中,AC恰是BD、DC、AB的第四比例项,所以考虑过C作CE∥AD,交BA的延长线于E,从而得到BD、DC、AB的第四比例项AE,这样,证明
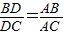
就可以转化成证AE=AC.
证明:过C作CE∥DA,交BA的延长线于E.
CE∥DA
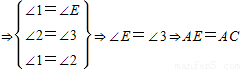
,
CE∥DA
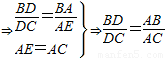
(1)上述证明过程中,用到了哪些定理?(写对两个定理即可)
(2)在上述分析、证明过程中,主要用到了下列三种数学思想的哪一种?选出一个填在后面的括号内.[]
①数形结合思想;
②转化思想;
③分类讨论思想.
(3)用三角形内角平分线性质定理解答问题:
已知:如图,△ABC中,AD是角平分线,AB=5cm,AC=4cm,BC=7cm.求BD的长.
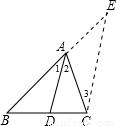
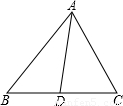
查看答案和解析>>
科目:czsx
来源:2000年山西省中考数学试卷(解析版)
题型:解答题
(2000•山西)请阅读下面材料,并回答所提出的问题.
三角形内角平分线性质定理:三角形的内角平分线分对边所得的两条线段和这个角的两边对应成比例.
已知:如图,△ABC中,AD是角平分线.
求证:
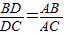
分析:要证
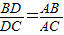
,一般只要证BD、DC与AB、AC或BD、AB与DC、AC所在三角形相似.现在B、D、C在一直线上,△ABD与△ADC不相似,需要考虑用别的方法换比.在比例式
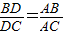
中,AC恰是BD、DC、AB的第四比例项,所以考虑过C作CE∥AD,交BA的延长线于E,从而得到BD、DC、AB的第四比例项AE,这样,证明
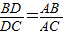
就可以转化成证AE=AC.
证明:过C作CE∥DA,交BA的延长线于E.
CE∥DA
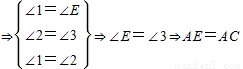
,
CE∥DA
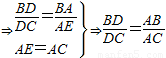
(1)上述证明过程中,用到了哪些定理?(写对两个定理即可)
(2)在上述分析、证明过程中,主要用到了下列三种数学思想的哪一种?选出一个填在后面的括号内.[]
①数形结合思想;
②转化思想;
③分类讨论思想.
(3)用三角形内角平分线性质定理解答问题:
已知:如图,△ABC中,AD是角平分线,AB=5cm,AC=4cm,BC=7cm.求BD的长.
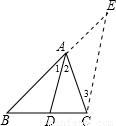
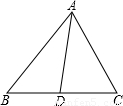
查看答案和解析>>
科目:czsx
来源:期末题
题型:解答题
阅读下面材料,按要求完成后面作业。
三角形内角平分线性质定理:三角形内角平分线分对边所得的两条线段和这个角的两边对应成比例。
已知:△ABC中,AD是角平分线(如图1), 求证:
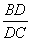
=
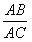
。
分析:要证
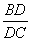
=
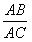
,一般只要证BD、DC与AB、AC或BD、AB与DC、AC所在的三角形相似,现在B、D、C在一条直线,△ABD与△ADC不相似,需要考虑用别的方法换比。
在比例式
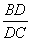
=
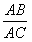
中,AC恰好是BD、DC、AB的第四比例项,所以考虑过C作CE∥AD交BA的延长线于E,从而得到BD、DC、AB的第四比例项AE,这样,证明
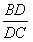
=
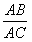
,就可转化证
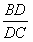
=
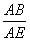
。
(1)完成证明过程:
证明:
(2)上述证明过程中,用到了哪些定理(写对两个即可)
答:用了:①____________;
②_____________。
(3)在上述分析和你的证明过程中,主要用到了下列三种数学思想的哪一种:①数形结合思想 ②转化思想 ③分类讨论思想
答:____________。
(4) 用三角形内角平分线定理解答问题:
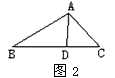
如图2,△ABC中,AD是角平分线,AB=5cm,AC=4cm,BD=7cm,求BC之长。
查看答案和解析>>
科目:czsx
来源:2000年全国中考数学试题汇编《相交线与平行线》(01)(解析版)
题型:解答题
(2000•山西)请阅读下面材料,并回答所提出的问题.
三角形内角平分线性质定理:三角形的内角平分线分对边所得的两条线段和这个角的两边对应成比例.
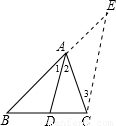
已知:如图,△ABC中,AD是角平分线.
求证:
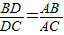
分析:要证
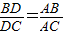
,一般只要证BD、DC与AB、AC或BD、AB与DC、AC所在三角形相似.现在B、D、C在一直线上,△ABD与△ADC不相似,需要考虑用别的方法换比.在比例式
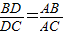
中,AC恰是BD、DC、AB的第四比例项,所以考虑过C作CE∥AD,交BA的延长线于E,从而得到BD、DC、AB的第四比例项AE,这样,证明
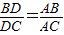
就可以转化成证AE=AC.
证明:过C作CE∥DA,交BA的延长线于E.
CE∥DA
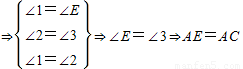
,
CE∥DA
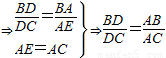
(1)上述证明过程中,用到了哪些定理?(写对两个定理即可)
(2)在上述分析、证明过程中,主要用到了下列三种数学思想的哪一种?选出一个填在后面的括号内.[]
①数形结合思想;
②转化思想;
③分类讨论思想.
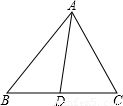
(3)用三角形内角平分线性质定理解答问题:
已知:如图,△ABC中,AD是角平分线,AB=5cm,AC=4cm,BC=7cm.求BD的长.
查看答案和解析>>
科目:czsx
来源:数学教研室
题型:044
请阅读下列材料,并回答所提出的问题。
三角形内角平分线性质定理:三角形的内角平分线分对边所得的线段与两
边对应成比例。
已知:如图,在△ABC中,AD是角平分线。
求证: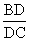 =
=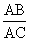 。
。

分析:要证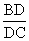 =
= ,一般只要证BD、DC与AB、AC
,一般只要证BD、DC与AB、AC
或BD、AB与DC、AC所在的三角形相似即可,现在点B、D、C
在一条直线上,△ABD与△ADC不相似,需要考虑用别的方法换比。在比例式
= 中,AC恰是BD、DC、AB的第四比例项,所以考虑过点C作CE//AD,交
中,AC恰是BD、DC、AB的第四比例项,所以考虑过点C作CE//AD,交
BA的延长线于点E,从而得到BD、DC、AB的第四比例项AE,这样,证明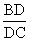 =
=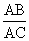
就可以转化成证AE=AC。
证明:过点C作CE//DA交BA的延长线于点E。
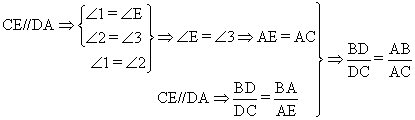 。
。
(1)在上述证明过程中,用到了哪些定理?(写对两个定理即可)
(2)在上述分析、证明过程中,主要利用到了下列三种数学思想中的哪一种?选出一
个填在后面的括号内………………………………………………………………( )
A. 数形结合思想
B. 转化思想
C. 分类讨论思想
(3)用三角形内角平分线性质定理解答问题。
如下图,已知在△ABC中,AD是角平分线,AB=5cm,AC=4cm,
BC=7cm,求BD的长。
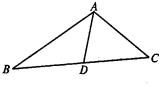
查看答案和解析>>
科目:czsx
来源:2000年全国中考数学试题汇编《三角形》(05)(解析版)
题型:解答题
(2000•山西)请阅读下面材料,并回答所提出的问题.
三角形内角平分线性质定理:三角形的内角平分线分对边所得的两条线段和这个角的两边对应成比例.
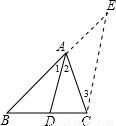
已知:如图,△ABC中,AD是角平分线.
求证:

分析:要证
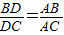
,一般只要证BD、DC与AB、AC或BD、AB与DC、AC所在三角形相似.现在B、D、C在一直线上,△ABD与△ADC不相似,需要考虑用别的方法换比.在比例式
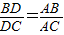
中,AC恰是BD、DC、AB的第四比例项,所以考虑过C作CE∥AD,交BA的延长线于E,从而得到BD、DC、AB的第四比例项AE,这样,证明
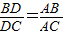
就可以转化成证AE=AC.
证明:过C作CE∥DA,交BA的延长线于E.
CE∥DA

,
CE∥DA
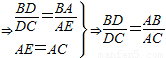
(1)上述证明过程中,用到了哪些定理?(写对两个定理即可)
(2)在上述分析、证明过程中,主要用到了下列三种数学思想的哪一种?选出一个填在后面的括号内.[]
①数形结合思想;
②转化思想;
③分类讨论思想.
(3)用三角形内角平分线性质定理解答问题:
已知:如图,△ABC中,AD是角平分线,AB=5cm,AC=4cm,BC=7cm.求BD的长.
查看答案和解析>>
科目:czsx
来源:
题型:
8、已知a=2.4cm,c=5.4cm,并且a,b,b,c成比例线段,那么b=
3.6
cm.
查看答案和解析>>
科目:czsx
来源:
题型:
已知a,b,c,d是成比例线段,且a=2,b=8,c=5,那么d=
20
20
.
查看答案和解析>>
科目:czsx
来源:
题型:
已知:a=3,b=4,c=5,请再添加一条线段,使这四条线段成比例线段.
查看答案和解析>>
科目:czsx
来源:
题型:
16、已知线段a=3cm,b=6cm,c=5cm,且a,b,d,c成比例线段,则d=
2.5
cm.
查看答案和解析>>
科目:czsx
来源:
题型:
已知a、b、c、d是成比例线段,其中a=5cm,b=3cm,c=6cm,则线段d=
3.6cm
3.6cm
.
查看答案和解析>>
科目:czsx
来源:
题型:
22、已知a,b,c,d是成比例线段,其中a=3cm,b=2cm,c=6cm,则d=
4;9;1
cm.
查看答案和解析>>
科目:czsx
来源:
题型:
已知a,b,c,d是成比例线段,其中a=2cm,b=3cm,d=6cm,则c=
.
查看答案和解析>>
科目:czsx
来源:
题型:
(1)已知a、b、c、d是成比例线段,其中a=3cm,b=2cm,c=6cm,求线段d的长.
(2)已知线段a、b、c,a=4cm,b=9cm,线段c是线段 a和b的比例中项.求线段c的长.
(3)已知y=y1+y2,y1与x成正比例,y2与x成反比例,且当x=1时,y=4,x=2时,y=5.
求:①y与x之间的函数关系式;②当x=4时,求y的值.
查看答案和解析>>
科目:czsx
来源:
题型:
已知如图中的两个四边形相似,找出图中的成比例线段,并用比例式表示.

查看答案和解析>>
科目:czsx
来源:
题型:
14、已知线段a、b、c、d是成比例线段,且a=2cm,b=0.6cm,c=4cm,那么d=
1.2
cm.
查看答案和解析>>
科目:czsx
来源:
题型:
已知四条线段a,b,c,d是成比例线段,即
=,下列说法错误的是( )
查看答案和解析>>

 E∥AD,交BA的延长线于E,从而得到BD、DC、AB的第四比例项AE,这样,证明
E∥AD,交BA的延长线于E,从而得到BD、DC、AB的第四比例项AE,这样,证明 []
[]
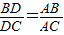 ,一般只要证BD、DC与AB、AC或BD、AB与DC、AC所在三角形相似.现在B、D、C在一直线上,△ABD与△ADC不相似,需要考虑用别的方法换比.在比例式
,一般只要证BD、DC与AB、AC或BD、AB与DC、AC所在三角形相似.现在B、D、C在一直线上,△ABD与△ADC不相似,需要考虑用别的方法换比.在比例式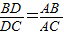 中,AC恰是BD、DC、AB的第四比例项,所以考虑过C作CE∥AD,交BA的延长线于E,从而得到BD、DC、AB的第四比例项AE,这样,证明
中,AC恰是BD、DC、AB的第四比例项,所以考虑过C作CE∥AD,交BA的延长线于E,从而得到BD、DC、AB的第四比例项AE,这样,证明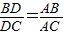 就可以转化成证AE=AC.
就可以转化成证AE=AC.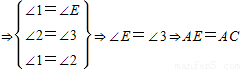 ,
,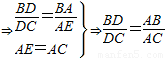


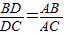
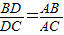 ,一般只要证BD、DC与AB、AC或BD、AB与DC、AC所在三角形相似.现在B、D、C在一直线上,△ABD与△ADC不相似,需要考虑用别的方法换比.在比例式
,一般只要证BD、DC与AB、AC或BD、AB与DC、AC所在三角形相似.现在B、D、C在一直线上,△ABD与△ADC不相似,需要考虑用别的方法换比.在比例式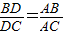 中,AC恰是BD、DC、AB的第四比例项,所以考虑过C作CE∥AD,交BA的延长线于E,从而得到BD、DC、AB的第四比例项AE,这样,证明
中,AC恰是BD、DC、AB的第四比例项,所以考虑过C作CE∥AD,交BA的延长线于E,从而得到BD、DC、AB的第四比例项AE,这样,证明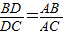 就可以转化成证AE=AC.
就可以转化成证AE=AC.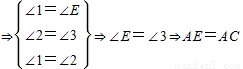 ,
,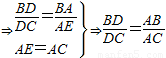


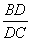 =
=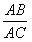 。
。 
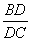 =
=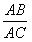 ,一般只要证BD、DC与AB、AC或BD、AB与DC、AC所在的三角形相似,现在B、D、C在一条直线,△ABD与△ADC不相似,需要考虑用别的方法换比。
,一般只要证BD、DC与AB、AC或BD、AB与DC、AC所在的三角形相似,现在B、D、C在一条直线,△ABD与△ADC不相似,需要考虑用别的方法换比。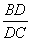 =
=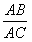 中,AC恰好是BD、DC、AB的第四比例项,所以考虑过C作CE∥AD交BA的延长线于E,从而得到BD、DC、AB的第四比例项AE,这样,证明
中,AC恰好是BD、DC、AB的第四比例项,所以考虑过C作CE∥AD交BA的延长线于E,从而得到BD、DC、AB的第四比例项AE,这样,证明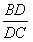 =
=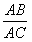 ,就可转化证
,就可转化证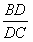 =
=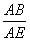 。
。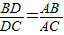
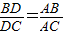 ,一般只要证BD、DC与AB、AC或BD、AB与DC、AC所在三角形相似.现在B、D、C在一直线上,△ABD与△ADC不相似,需要考虑用别的方法换比.在比例式
,一般只要证BD、DC与AB、AC或BD、AB与DC、AC所在三角形相似.现在B、D、C在一直线上,△ABD与△ADC不相似,需要考虑用别的方法换比.在比例式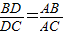 中,AC恰是BD、DC、AB的第四比例项,所以考虑过C作CE∥AD,交BA的延长线于E,从而得到BD、DC、AB的第四比例项AE,这样,证明
中,AC恰是BD、DC、AB的第四比例项,所以考虑过C作CE∥AD,交BA的延长线于E,从而得到BD、DC、AB的第四比例项AE,这样,证明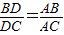 就可以转化成证AE=AC.
就可以转化成证AE=AC.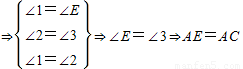 ,
,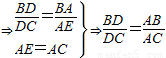


![]() =
=![]() 。
。
![]() =
=![]() ,一般只要证BD、DC与AB、AC
,一般只要证BD、DC与AB、AC![]()
![]() 中,AC恰是BD、DC、AB的第四比例项,所以考虑过点C作CE//AD,交
中,AC恰是BD、DC、AB的第四比例项,所以考虑过点C作CE//AD,交![]() =
=![]()
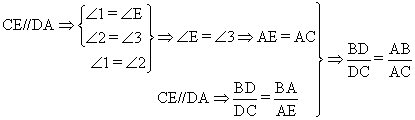 。
。

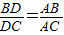 ,一般只要证BD、DC与AB、AC或BD、AB与DC、AC所在三角形相似.现在B、D、C在一直线上,△ABD与△ADC不相似,需要考虑用别的方法换比.在比例式
,一般只要证BD、DC与AB、AC或BD、AB与DC、AC所在三角形相似.现在B、D、C在一直线上,△ABD与△ADC不相似,需要考虑用别的方法换比.在比例式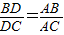 中,AC恰是BD、DC、AB的第四比例项,所以考虑过C作CE∥AD,交BA的延长线于E,从而得到BD、DC、AB的第四比例项AE,这样,证明
中,AC恰是BD、DC、AB的第四比例项,所以考虑过C作CE∥AD,交BA的延长线于E,从而得到BD、DC、AB的第四比例项AE,这样,证明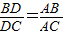 就可以转化成证AE=AC.
就可以转化成证AE=AC. ,
,