精英家教网 >
试题搜索列表 >如图,(1)2)在直角坐标系中,第一象限AB方向放有一个平面镜,一束光线CD经过反射的反射光线是DE,法线DH交y轴于点H.交x轴于点F(∠DCE>∠DEC),若平面镜AB绕点D旋转,则是否存在一个正整数k,使∠DCE -∠DEC = k ∠OHF.若存在,请求出k值,若不存在,请说明理由(3)在(2)的条件下,在E点处水平放第二个平面镜,如图所示,光线CD经过二次反射后,反射光线为EG.射线CD、EG的反向延长线交于点P.求证:∠P = 2∠OHF
如图,(1)2)在直角坐标系中,第一象限AB方向放有一个平面镜,一束光线CD经过反射的反射光线是DE,法线DH交y轴于点H.交x轴于点F(∠DCE>∠DEC),若平面镜AB绕点D旋转,则是否存在一个正整数k,使∠DCE -∠DEC = k ∠OHF.若存在,请求出k值,若不存在,请说明理由(3)在(2)的条件下,在E点处水平放第二个平面镜,如图所示,光线CD经过二次反射后,反射光线为EG.射线CD、EG的反向延长线交于点P.求证:∠P = 2∠OHF答案解析
科目:czsx
来源:
题型:
(2012•朝阳)在不透明的箱子里放有4个乒乓球,每个乒乓球上分别写有数字1、2、3、4,从箱中摸出一个球记下数字后放回箱中,摇匀后再摸出一个记下数字.若将第一次摸出的球上的数字记为点的横坐标,第二次摸出球上的数字记为
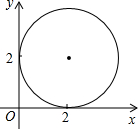
点的纵坐标.
(1)请用列表法或树状图法写出两次摸球后所有可能的结果.
(2)求这样的点落在如图所示的圆内的概率(注:图中圆心在直角坐标系中的第一象限内,并且分别于x轴、y轴切于点(2,0)和(0,2)两点).
查看答案和解析>>
科目:czsx
来源:2012年人教版七年级下第六章第二节坐标方法的简单应用练习卷(解析版)
题型:解答题
如图

(1)请写出在直角坐标系中的房子的A、B、C、D、E、F、G的坐标。
(2)源源想把房子向下平移3个单位长度,你能帮他办到吗?请作出相应图案,并写出平移后的7个点的坐标。
查看答案和解析>>
科目:czsx
来源:2010-2011学年山西省初三3月份月考数学卷
题型:解答题
如图
(1)请写出在直角坐标系中的房子的A、B、C、D、E、F、G的坐标。
(2)源源想把房子向下平移3个单位长度,你能帮他办到吗?请作出相应图案,并写出平移后的7个点的坐标。

查看答案和解析>>
科目:czsx
来源:2013年湖北省随州市曾都区实验中学中考数学模拟试卷(二)(解析版)
题型:解答题
在不透明的箱子里放有4个乒乓球,每个乒乓球上分别写有数字1、2、3、4,从箱中摸出一个球记下数字后放回箱中,摇匀后再摸出一个记下数字.若将第一次摸出的球上的数字记为点的横坐标,第二次摸出球上的数字记为点的纵坐标.
(1)请用列表法或树状图法写出两次摸球后所有可能的结果.
(2)求这样的点落在如图所示的圆内的概率(注:图中圆心在直角坐标系中的第一象限内,并且分别于x轴、y轴切于点(2,0)和(0,2)两点).

查看答案和解析>>
科目:czsx
来源:2013年湖北省随州市中考数学模拟试卷(二)(解析版)
题型:解答题
在不透明的箱子里放有4个乒乓球,每个乒乓球上分别写有数字1、2、3、4,从箱中摸出一个球记下数字后放回箱中,摇匀后再摸出一个记下数字.若将第一次摸出的球上的数字记为点的横坐标,第二次摸出球上的数字记为点的纵坐标.
(1)请用列表法或树状图法写出两次摸球后所有可能的结果.
(2)求这样的点落在如图所示的圆内的概率(注:图中圆心在直角坐标系中的第一象限内,并且分别于x轴、y轴切于点(2,0)和(0,2)两点).

查看答案和解析>>
科目:czsx
来源:2012年辽宁省朝阳市中考数学试卷(解析版)
题型:解答题
在不透明的箱子里放有4个乒乓球,每个乒乓球上分别写有数字1、2、3、4,从箱中摸出一个球记下数字后放回箱中,摇匀后再摸出一个记下数字.若将第一次摸出的球上的数字记为点的横坐标,第二次摸出球上的数字记为点的纵坐标.
(1)请用列表法或树状图法写出两次摸球后所有可能的结果.
(2)求这样的点落在如图所示的圆内的概率(注:图中圆心在直角坐标系中的第一象限内,并且分别于x轴、y轴切于点(2,0)和(0,2)两点).

查看答案和解析>>
科目:czsx
来源:
题型:044
阅读:我们知道,在数轴上,x=1表示一个点,而在平面直角坐标系中,x=1表示一条直线;我们还知道,以二元一次方程2x-y+1=0的所有解为坐标的点组成的图形就是一次函数y=2x+1的图象,它也是一条直线,如图11-3-4(1).

在直角坐标系中,x≤1表示一个平面区域,即直线x=1以及它左侧的部分,如图11-3-4(2);
y≤2x+1也表示一个平面区域,即直线y=2x+1以及它下方的部分,如图11-3-4(3).
回答下列问题:
(1)在直角坐标系中,用作图象的方法求出方程组 的解;
的解;
(2)用阴影表示 所围成的区域.
所围成的区域.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
在不透明的箱子里放有4个乒乓球,每个乒乓球上分别写有数字1、2、3、4,从箱中摸出一个球记下数字后放回箱中,摇匀后再摸出一个记下数字.若将第一次摸出的球上的数字记为点的横坐标,第二次摸出球上的数字记为 点的纵坐标.
点的纵坐标.
(1)请用列表法或树状图法写出两次摸球后所有可能的结果.
(2)求这样的点落在如图所示的圆内的概率(注:图中圆心在直角坐标系中的第一象限内,并且分别于x轴、y轴切于点(2,0)和(0,2)两点).
查看答案和解析>>
科目:czsx
来源:
题型:
如图
(1)请写出在直角坐标系中的房子的A、B、C、D、E、F、G的坐标。
(2)源源想把房子向下平移3个单位长度,你能帮他办到吗?请作出相应图案,并写出平移后的7个点的坐标。
![]()
查看答案和解析>>
科目:czsx
来源:2011年广东省初中数学竞赛题
题型:解答题
如图
(1)请写出在直角坐标系中的房子的A、B、C、D、E、F、G的坐标。
(2)源源想把房子向下平移3个单位长度,你能帮他办到吗?请作出相应图案,并写出平移后的7个点的坐标。
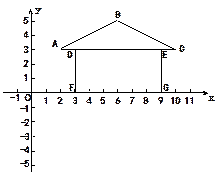
查看答案和解析>>
科目:czsx
来源:
题型:

23、如图,在直角坐标系中,第一次将△OAB变换成△OA
1B
1,第二次将△OA
1B
1变换成△OA
2B
2,第三次将△OA
2B
2变换成△OA
3B
3…
已知:A(1,3),A
1(2,3),A
2(4,3),A
3(8,3),B(2,0),B
1(4,0),B
2(8,0),B(16,0).观察每次变换前后的三角形有何变化,按照变换规律,求第五次变换后得到的三角形A
5的坐标和B
5的坐标.
查看答案和解析>>
科目:czsx
来源:
题型:
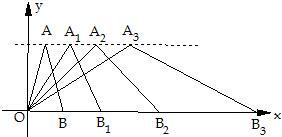
22、如图:在直角坐标系中,第一次将△AOB变换成△OA
1B
1,第二次将三角形变换成△OA
2B
2,第三次将△OA
2B
2,变换成△OA
3B
3,已知A(1,3),A
1(3,3),A
2(5,3),A
3(7,3);B(2,0),B
1(4,0),B
2(8,0),B
3(16,0).
(1)观察每次变换前后的三角形有何变化,找出规律,按此变化规律再将△OA
3B
3变换成△OA
4B
4,则A
4的坐标是
(9,3)
,B
4的坐标是
(32,0)
.
(2)若按(1)找到的规律将△OAB进行了n次变换,得到△OA
nB
n,比较每次变换中三角形顶点有何变化,找出规律,推测A的坐标是
(2n+1,3)
,B的坐标是
(2n,0)
.
查看答案和解析>>
科目:czsx
来源:
题型:
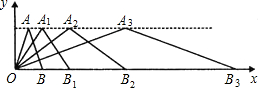
如图,在直角坐标系中,第一次将△OAB变换成△OA
1B
1,第二次将△OA
1B
1变换成△OA
2B
2,第三次将△OA
2B
2变换成△OA
3B
3,已知A(1,3),A
1(2,3),A
2(4,3),A
3(8,3),B(2,0),B
1(4,0),B
2(8,0),B
3(16,0).将△OAB进行n次变换得到△OA
nB
n,则A
n(
2n
2n
,
3
3
),B
n(
2n+1
2n+1
,
0
0
).
查看答案和解析>>
科目:czsx
来源:
题型:
如图所示,在直角坐标系中,第一次将△OAB变换成△OA
1B
1,第二次将△OA
1B
1变换成△OA
2B
2,第三次将△OA
2B
2变换成△OA
3B
3,已知A(1,3),A
1(2,3),A
2(4,3),A
3(8,3),B(2,0),B
1(4,0),B
2(8,0),B
3(16,0).

(1)观察每次变换前后的三角形有何变化,找出规律,按此变换规律将△OA
4B
4变换成△OA
5B
5,则A
5的坐标是
(32,3)
(32,3)
,B
5的坐标是
(64,0)
(64,0)
.
(2)若按第(1)题的规律将△OAB进行了n次变换,得到△OA
nB
n,比较每次变换中三角形顶点坐标有何变化,找出规律,请推测A
n的坐标是
(2n,3)
(2n,3)
,B
n的坐标是
(2n+1,0)
(2n+1,0)
.
查看答案和解析>>
科目:czsx
来源:
题型:
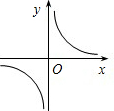
已知反比例函数y
1=
的图象如图所示,
(1)在同一坐标系中画出y
2=
x-1的图象;
(2)写出反比例函数y
1=
和一次函数y
2═
x-1这两个函数的图象的交点的坐标并验证其正确性;
(3)观察图象,写出当x为何值时,函数值y
1>y
2?
查看答案和解析>>
科目:czsx
来源:
题型:阅读理解
(1)完成下面的证明:
已知:如图1,AB∥CD∥GH,EG平分∠BEF,FG平分∠EFD.
求证:∠EGF=90°.
证明:∵HG∥AB,(已知)
∴∠1=∠3. (
两直线平行,内错角相等
两直线平行,内错角相等
)
又∵HG∥CD,(已知)
∴∠2=∠4. (
两直线平行,内错角相等
两直线平行,内错角相等
)
∵AB∥CD,(已知)
∴∠BEF+
∠EFD
∠EFD
=180°.(
两直线平行,同旁内角互补
两直线平行,同旁内角互补
)
又∵EG平分∠BEF,(已知)
∴∠1=
∠
BEH
BEH
.(
角平分线定义
角平分线定义
)
又∵FG平分∠EFD,(已知)
∴∠2=
∠
EFD
EFD
.(
角平分线定义
角平分线定义
)
∴∠1+∠2=
(
∠BEH
∠BEH
+
∠EFD
∠EFD
).
∴∠1+∠2=90°.
∴∠3+∠4=90°.(
等量代换
等量代换
).即∠EGF=90°.
(2)如图2,已知∠ACB=90°,那么∠A的余角是哪个角呢?答:
∠B
∠B
;
小明用三角尺在这个三角形中画了一条高CD(点D是垂足),得到图3,
①请你帮小明在图中画出这条高;
②在图中,小明通过仔细观察、认真思考,找出了三对余角,你能帮小明把它们写出来吗?答:a
∠ACD与∠BCD
∠ACD与∠BCD
;b
∠A与∠ACD
∠A与∠ACD
;c
∠B与∠BCD
∠B与∠BCD
.
③∠ACB,∠ADC,∠CDB都是直角,所以∠ACB=∠ADC=∠CDB,小明还发现了另外两对相等的角,请你也仔细地观察、认真地思考分析,试一试,能发现吗?把它们写出来,并请说明理由.
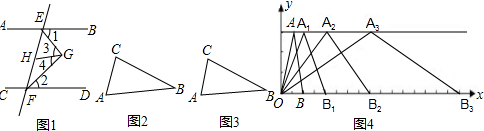
(3)在直角坐标系中,第一次将△OAB变换成OA
1B
1,第二次将△OA
1B
1变换成△OA
2B
2,第三次将△OA
2B
2变换成△OA
3B
3,已知A(1,3),A
1(2,3),A
2(4,3),A
3(8,3),B(2,0),B
1(4,0),B
2(8,0),B
3(16,0).
①观察每次变换前后的三角形有何变化,找出规律,按此规律再将△OA
3B
3变换成△OA
4B
4,则A
4的坐标为
(16,3)
(16,3)
,B
4的坐标为
(32,0)
(32,0)
.
②按以上规律将△OAB进行n次变换得到△A
nB
n,则可知A
n的坐标为
(2n,3)
(2n,3)
,B
n的坐标为
(2n+1,0)
(2n+1,0)
.
③可发现变换的过程中A、A
1、A
2、…、A
n纵坐标均为
3
3
.
查看答案和解析>>
科目:czsx
来源:
题型:
如图:在直角坐标系中,第一次将△AOB变换成△OA
1B
1,第二次将三角形变换成△OA
2B
2,第三次将△OA
2B
2,变换成△OA
3B
3,已知A(1,3),A
1(3,3),A
2(5,3),A
3(7,3);B(2,0),B
1(4,0),B
2(8,0),B
3(16,0).
(1)观察每次变换前后的三角形有何变化,找出规律,按此变化规律再将△OA
3B
3变换成△OA
4B
4,则A
4的坐标是(
9
9
,
3
3
),B
4的坐标是(
32
32
,
0
0
).
(2)若按(1)找到的规律将△OAB进行了n次变换,得到△OA
nB
n,比较每次变换中三角形顶点有何变化,找出规律,推测A
n的坐标是(
2n+1
2n+1
,
3
3
),B
n的坐标是(
2n+1
2n+1
,
0
0
).

查看答案和解析>>
科目:czsx
来源:
题型:
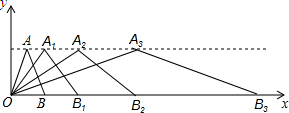
如图所示,在直角坐标系中,第一次将△OAB变换成△OA
1B
1第二次将OA
1B
1变换成△OA
2B
2,第三次将△OA
2B
2变换成△OA
3B
3,已知A(1,3),A
1(2,3),A
2(4,3),A
3(8,3),B(2,0),B
1(4,0),B
2(8,0),B
3(16,0).
(1)求△OAB的面积;
(2)写出△OA
4B
4的各个顶点的坐标;
(3)按此图形变化规律,你能写出△OA
nB
n的面积与△OAB的面积的大小关系吗?
查看答案和解析>>
科目:czsx
来源:
题型:

如图,将△ABC和△DEF放置在正方形网格中,求证:AB=DE.
查看答案和解析>>
科目:czsx
来源:
题型:
(1)尺规作图.
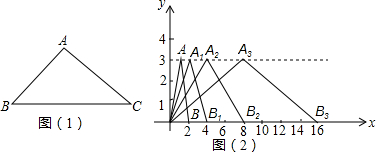
要求:写出作法(用词准确精炼);保留作图痕迹(图形清晰,规范),已知:如图△ABC.
求作:△ABC的内角平分线AD.
作法:
(2)如图2,在直角坐标系中,第一次将△OAB变换成△OA
1B
1,第二次将△OA
1B
1变换成△OA
2B
2,-----依此类推.已知A(1,3),A
1(2,3),A
2(4,3),A
3(8,3),…;B(2,0),B
1(4,0),B
2(8,0),B
3(16,0),….
①观察每次变换三角形的顶点变化规律,按此变换规律,经过
6
6
次变换后,A、B的对应点坐标分别为(64,3)、(128,0).
②若按第①小题找到的规律将△OAB进行了n次变换,得到△OA
nB
n,推测A
n的坐标是
(2n,3)
(2n,3)
,B
n的坐标是
(2n+1,0)
(2n+1,0)
.
查看答案和解析>>

 点的纵坐标.
点的纵坐标.





![]() 的解;
的解; 所围成的区域.
所围成的区域. 点的纵坐标.
点的纵坐标.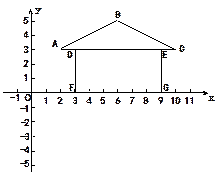
 23、如图,在直角坐标系中,第一次将△OAB变换成△OA1B1,第二次将△OA1B1变换成△OA2B2,第三次将△OA2B2变换成△OA3B3…
23、如图,在直角坐标系中,第一次将△OAB变换成△OA1B1,第二次将△OA1B1变换成△OA2B2,第三次将△OA2B2变换成△OA3B3…


 已知反比例函数y1=
已知反比例函数y1=


