已知抛物线的顶点为(3,),且与x轴两交点间的距离为4答案解析
科目:czsx
来源:河北省同步题
题型:单选题
已知抛物线y=x2+2(k+1)x+k2与x轴两交点的横坐标的和大于-4,则
查看答案和解析>>
科目:czsx
来源:新课程 新理念 新思维·同步练习篇·数学 九年级下册(苏教版) 苏教版
题型:044
已知抛物线的顶点为(3,-2),且与x轴两交点间的距离为4.求对应的二次函数的关系式.
查看答案和解析>>
科目:czsx
来源:
题型:044
根据下列条件,分别求出对应的二次函数的关系式.
(1)已知二次函数的图象经过点A(0,-1)、B(1,0)、C(-1,2);
(2)已知抛物线的顶点为(1,-3),且与y轴交于点(0,1);
(3)已知抛物线与x轴交于点M(-3,0)、N(5,0),且与y轴交于点(0,-3);
(4)已知抛物线的顶点为(3,-2),且与x轴两交点间的距离为4.
查看答案和解析>>
科目:czsx
来源:
题型:
已知关于x的方程mx2-(3m-1)x+2m-2=0.
(1)求证:无论m取任何实数时,方程恒有实数根;
(2)若m为整数,且抛物线y=mx2-(3m-1)x+2m-2与x轴两交点间的距离为2,求抛物线的解析式;
(3)若直线y=x+b与(2)中的抛物线没有交点,求b的取值范围.
查看答案和解析>>
科目:czsx
来源:融安县二模
题型:解答题
已知关于x的方程mx2-(3m-1)x+2m-2=0.
(1)求证:无论m取任何实数时,方程恒有实数根;
(2)若m为整数,且抛物线y=mx2-(3m-1)x+2m-2与x轴两交点间的距离为2,求抛物线的解析式;
(3)若直线y=x+b与(2)中的抛物线没有交点,求b的取值范围.
查看答案和解析>>
科目:czsx
来源:2012年广西柳州市融安县中考数学二模试卷(解析版)
题型:解答题
已知关于x的方程mx2-(3m-1)x+2m-2=0.
(1)求证:无论m取任何实数时,方程恒有实数根;
(2)若m为整数,且抛物线y=mx2-(3m-1)x+2m-2与x轴两交点间的距离为2,求抛物线的解析式;
(3)若直线y=x+b与(2)中的抛物线没有交点,求b的取值范围.
查看答案和解析>>
科目:czsx
来源:2011年北京市顺义区中考数学二模试卷(解析版)
题型:解答题
已知关于x的方程mx2-(3m-1)x+2m-2=0.
(1)求证:无论m取任何实数时,方程恒有实数根;
(2)若m为整数,且抛物线y=mx2-(3m-1)x+2m-2与x轴两交点间的距离为2,求抛物线的解析式;
(3)若直线y=x+b与(2)中的抛物线没有交点,求b的取值范围.
查看答案和解析>>
科目:czsx
来源:2012-2013学年北京市石景山区实验中学九年级(上)期中数学试卷(解析版)
题型:解答题
已知关于x的方程mx2-(3m-1)x+2m-2=0.
(1)求证:无论m取任何实数时,方程恒有实数根;
(2)若m为整数,且抛物线y=mx2-(3m-1)x+2m-2与x轴两交点间的距离为2,求抛物线的解析式;
(3)若直线y=x+b与(2)中的抛物线没有交点,求b的取值范围.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
已知关于x的方程mx2-(3m-1)x+2m-2=0.
(1)求证:无论m取任何实数时,方程恒有实数根;
(2)若m为整数,且抛物线y=mx2-(3m-1)x+2m-2与x轴两交点间的距离为2,求抛物线的解析式;
(3)若直线y=x+b与(2)中的抛物线没有交点,求b的取值范围.
查看答案和解析>>
科目:czsx
来源:
题型:
已知二次函数的图象与x轴两交点间的距离为2,若将图象沿y轴方向向上平移3个单位,则图象恰好经过原点,且与x轴两交点间的距离为4,求原二次函数的表达式.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
已知二次函数的图象与x轴两交点间的距离为2,若将图象沿y轴方向向上平移3个单位,则图象恰好经过原点,且与x轴两交点间的距离为4,求原二次函数的表达式.
查看答案和解析>>
科目:czsx
来源:2010年10月浙江省杭州市滨江区九年级(上)月考数学试卷(解析版)
题型:解答题
已知二次函数的图象与x轴两交点间的距离为2,若将图象沿y轴方向向上平移3个单位,则图象恰好经过原点,且与x轴两交点间的距离为4,求原二次函数的表达式.
查看答案和解析>>
科目:czsx
来源:
题型:
已知抛物线y=ax
2+bx+c(a<0)与x轴交于A、B两点,点A在x轴的负半轴上,点B在x轴的正半轴上,又此抛物线交y轴于点C,连AC、BC,且满足△OAC的面积与△OBC的面积之差等于两线段OA与OB的积(即S
△OAC-S
△OBC=OA•OB)
(1)求b的值;
(2)若tan∠CAB=
,抛物线的顶点为点P,是否存在这样的抛物线,使得△PAB的外接圆半径为
?若存在,求出这样的抛物线的解析式;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
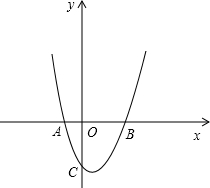
已知抛物线y=ax
2-2ax+n(a>0)与x轴交于A(x
1,0)、B(x
2,0),交y轴的负半轴于点C,且x
1<x
2,OC=OB,S
△ABC=6
(1)求此抛物线的解析式;
(2)若D为抛物线的顶点,P为抛物线上的点,且在第二象限,S
△PBD=15,求点P的坐标;
(3)在(2)的条件下,在抛物线上是否存在点M,使△MBD为直角三角形?若存在,求出所有符合条件的M点坐标,若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
已知抛物线与x轴两交点间的距离为4,与y轴交于点C,其顶点为(-1,4),求△ABC的面积.
查看答案和解析>>
科目:czsx
来源:
题型:
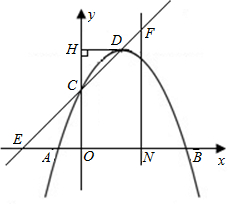
已知抛物线y=ax
2-2ax-3a(a<0)与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点D为抛物线的顶点.
(1)求A、B的坐标;
(2)过点D作DH丄y轴于点H,若DH=HC,求a的值和直线CD的解析式;
(3)在第(2)小题的条件下,直线CD与x轴交于点E,过线段OB的中点N作NF丄x轴,并交直线CD于点F,则直线NF上是否存在点M,使得点M到直线CD的距离等于点M到原点O的距离?若存在,求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
(2013•厦门质检)已知抛物线y=x
2-2bx+c(c>0)与y轴的交点为A,顶点为M(m,n).
(1)若c=2b-1,点M在x轴上,求c的值.
(2)若直线
y=-x+t过点A,且与x轴交点为B,直线和抛物线的另一交点为P,且P为线段AB的中点.当n取得最大值时,求抛物线的解析式.
查看答案和解析>>
科目:czsx
来源:
题型:
已知抛物线y=x
2-(2m+4)x+m
2-10与x轴交于A、B两点,C是抛物线的顶点.
(1)用配方法求顶点C的坐标(用含m的代数式表示);
(2)若AB的长为
2,求抛物线的解析式;
(3)怎样平移(2)中的这条抛物线,使它在x轴上截得的线段长为4?
查看答案和解析>>
科目:czsx
来源:
题型:
已知抛物线y=-x
2+(m-4)x+2m+4与x轴相交于A(x
1,0),B(x
2,0)与y轴交于点C,且x
1=-2x
2(x
1<x
2),点A关于y轴的对称点为D.
(1)确定A,B,C三点的坐标;
(2)求过B,C,D三点的抛物线的解析式;
(3)若y=3与(2)小题中所求抛物线交于M,N,以MN为一边,抛物线上任一点P(x,y)为顶点作为平行四边形,若平行四边形面积为S,写出S与P点纵坐标y的函数关系式;
(4)当
<x<4时,(3)小题中平行四边形的面积是否有最大值?若有,请求出;若无,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
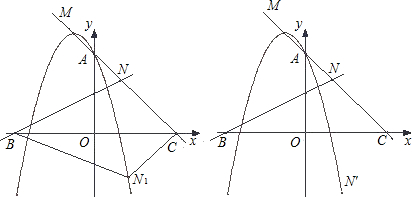
已知抛物线y=-x
2-2x+a(a>0)与y轴相交于点A,顶点为M.直线y=
x+a与x轴相交于B点,与直线AM相交于N点;直线AM与x轴相交于C点
(1)求M的坐标与MA的解析式(用字母a表示);
(2)如图,将△NBC沿x轴翻折,若N点的对应点N′恰好落在抛物线上,求a的值;
(3)在抛物线y=-x
2-2x+a(a>0)上是否存在一点P,使得以P、B、C、N为顶点的四边形是平行四边形?若存在,求出a的值;若不存在,说明理由.
查看答案和解析>>


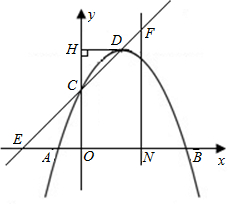 已知抛物线y=ax2-2ax-3a(a<0)与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点D为抛物线的顶点.
已知抛物线y=ax2-2ax-3a(a<0)与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点D为抛物线的顶点.