
科目:czsx 来源:2011学年浙江省八年级上学期期中考试数学卷 题型:解答题
已知,如图,∠1=∠2,且∠1=∠3,阅读并补充下列推理过程,在括号中填写理由:
解:∵∠1=∠2( )
∴ ∥ ( )
又∵∠1=∠3(已知)
∴∠2=∠3
∴ ∥ ( )
∴∠1+∠4=180° ( )

科目:czsx 来源:2011年泰顺三中八年级第一学期期中考试数学卷 题型:解答题
已知,如图,∠1=∠2,且∠1=∠3,阅读并补充下列推理过程,在括号中填写理由:

解:∵∠1=∠2( )
∴ ∥ ( )
又∵∠1=∠3(已知)
∴∠2=∠3
∴ ∥ ( )
∴∠1+∠4=180° ( )
科目:czsx 来源:2012-2013学年浙江宁波地八年级第一次质量评估数学试卷(解析版) 题型:解答题
已知,如图,∠1=∠2,且∠1=∠3,阅读并补充下列推理过程,在括号中填写理由:

解:∵∠1=∠2( )
∴ ∥ ( )
又∵∠1=∠3(已知)
∴∠2=∠3
∴ ∥ ( )
∴∠1+∠4=180° ( )
科目:czsx 来源:2015届浙江省建德市七年级3月月考数学试卷(解析版) 题型:解答题
如图,已知EF∥AD,∠1=∠2,∠BAC=65º.请将求∠AGD的过程填写完整.

解:∵EF∥AD
∴∠2= ( )
又∵∠1=∠2
∴∠1=∠3
∴AB∥ ( )
∴∠BAC+ =180º.
又∵∠BAC=65º
∴∠AGD= .
科目:czsx 来源: 题型:
已知,如图,∠1=∠2,且∠1=∠3,阅读并补充下列推理过程,在括号中填写理由:
解:∵∠1=∠2( )
∴ ∥ ( )
又∵∠1=∠3(已知)
∴∠2=∠3
∴ ∥ ( )
∴∠1+∠4=180° ( )
科目:czsx 来源:2014届云南玉溪洛河民族中学初一下学期期中考试数学试卷(解析版) 题型:填空题
如图,已知∠1+∠2=180°,∠3=∠B,则∠EDG与∠DGB相等吗?下面是王冠同学的部分推导过程,请你帮他在括号内填上推导依据或内容。

解:∵∠1+∠2=180°(已知)
∠1+∠DFE=180°
∴∠2=
∴EF∥AB( )
∴∠3=
∵∠3=∠B ( )
∴∠B=∠ADE( )
∴DE∥BC( )
∴∠EDG=∠DGB( )
科目:czsx 来源:2012-2013学年浙江临安於潜第一初级中学八年级10月数学试卷(带解析) 题型:解答题
如图,已知EF∥AD,∠1 =∠2,∠BAC=65º.请将求∠AGD的过程填写完整.
解:∵EF∥AD( )
∴∠2= ( )
又∵∠1=∠2
∴∠1=∠3( )
∴AB∥ ( )
∴∠BAC+ =180º.
又∵∠BAC=65º
∴∠AGD= .
科目:czsx 来源:2012-2013学年浙江宁波地八年级第一次质量评估数学试卷(带解析) 题型:解答题
已知,如图,∠1=∠2,且∠1=∠3,阅读并补充下列推理过程,在括号中填写理由: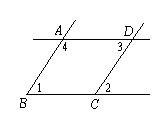
解:∵∠1=∠2( )
∴ ∥ ( )
又∵∠1=∠3(已知)
∴∠2=∠3
∴ ∥ ( )
∴∠1+∠4=180° ( )
科目:czsx 来源:2011-2012学年浙江省菁才中学八年级上学期期中考试数学试卷(带解析) 题型:解答题
如图,EF∥AD,∠1 =∠2,∠BAC = 70°。将求∠AGD的过程填写完整。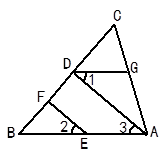
解:∵EF∥AD( 已知 )
∴∠2 = ( )
又∵ ∠1=∠2( 已知 )
∴ ∠1 = ∠3
∴AB∥ ( )
∴∠BAC + = 180°。
又∵∠BAC= 70°
∴∠AGD = 。
科目:czsx 来源: 题型:
科目:czsx 来源:2011-2012学年云南玉溪洛河民族中学初一下学期期中考试数学试卷(带解析) 题型:填空题
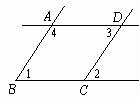
如图,已知∠1+∠2=180°,∠3=∠B,则∠EDG与∠DGB相等吗?下面是王冠同学的部分推导过程,请你帮他在括号内填上推导依据或内容。
解:∵∠1+∠2=180°(已知)
∠1+∠DFE=180°
∴∠2=
∴EF∥AB( )
∴∠3=
∵∠3=∠B ( )
∴∠B=∠ADE( )
∴DE∥BC( )
∴∠EDG=∠DGB( )
科目:czsx 来源:2012-2013学年浙江省建德市李家镇初级中学七年级3月月考数学试卷(带解析) 题型:解答题
如图,已知EF∥AD,∠1=∠2,∠BAC=65º.请将求∠AGD的过程填写完整.
解:∵EF∥AD
∴∠2= ( )
又∵∠1=∠2
∴∠1=∠3
∴AB∥ ( )
∴∠BAC+ =180º.
又∵∠BAC=65º
∴∠AGD= .
科目:czsx 来源:2013届浙江省八年级上学期期中考试数学试卷(解析版) 题型:解答题
如图,EF∥AD,∠1 =∠2,∠BAC = 70°。将求∠AGD的过程填写完整。

解:∵EF∥AD( 已知 )
∴∠2 = ( )
又∵ ∠1=∠2( 已知 )
∴ ∠1 = ∠3
∴AB∥ ( )
∴∠BAC + = 180°。
又∵∠BAC= 70°
∴∠AGD = 。
科目:czsx 来源:2012-2013学年江西省吉安市朝宗实验学校七年级下学期第一次段考数学试卷(带解析) 题型:解答题
如图,已知∠A=∠C,∠1+∠2=180°,试问:∠B与∠F有什么关系?为什么?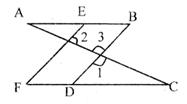
解:∠B=∠F,理由如下:
∵∠A=∠C
∴ ∥ ( )
∴∠BDC=∠B ( )
∵∠1+∠2=180°
且∠1+∠3 ( )
∴∠3+∠2=180°
∴ ∥ ( )
∴∠BDC= ( )
∴∠B=∠F ( )
科目:czsx 来源:2012-2013学年浙江临安於潜第一初级中学八年级10月数学试卷(解析版) 题型:解答题
如图,已知EF∥AD,∠1 =∠2,∠BAC=65º.请将求∠AGD的过程填写完整.
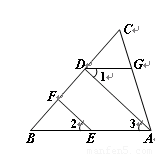
解:∵EF∥AD( )
∴∠2= ( )
又∵∠1=∠2
∴∠1=∠3( )
∴AB∥ ( )
∴∠BAC+ =180º.
又∵∠BAC=65º
∴∠AGD= .
科目:czsx 来源:2015届浙江省建德市七年级下学期期中数学卷(解析版) 题型:填空题
如图,点E在直线DF上,点B在直线AC上,若∠1=∠2,∠3=∠4,则∠A=∠F,请说明理由.

解:∵∠1=∠2(已知)
∠2=∠DGF( )
∴∠1=∠DGF
∴BD∥CE( )
∴∠3+∠C=180º( )
又∵∠3=∠4(已知)
∴∠4+∠C=180º
∴ ∥ (同旁内角互补,两直线平行)
∴∠A=∠F( )
科目:czsx 来源: 题型:
如图,已知∠1+∠2=180°,∠3=∠B,则∠EDG与∠DGB相等吗?下面是王冠同学的部分推导过程,请你帮他在括号内填上推导依据或内容。

解:∵∠1+∠2=180°(已知)
∠1+∠DFE=180°
∴∠2=
∴EF∥AB( )
∴∠3=
∵∠3=∠B ( )
∴∠B=∠ADE( )
∴DE∥BC( )
∴∠EDG=∠DGB( )
科目:czsx 来源: 题型:
已知,如图,∠1=∠2,且∠1=∠3,阅读并补充下列推理过程,在括号中填写理由:

解:∵∠1=∠2( )
∴ ∥ ( )
又∵∠1=∠3(已知)
∴∠2=∠3
∴ ∥ ( )
∴∠1+∠4=180° ( )
科目:czsx 来源: 题型:
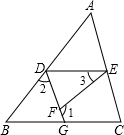
科目:czsx 来源:2012-2013学年浙江省建德市李家镇初级中学七年级下学期期中数学卷(带解析) 题型:填空题
如图,点E在直线DF上,点B在直线AC上,若∠1=∠2,∠3=∠4,则∠A=∠F,请说明理由.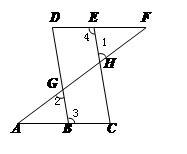
解:∵∠1=∠2(已知)
∠2=∠DGF( )
∴∠1=∠DGF
∴BD∥CE( )
∴∠3+∠C=180º( )
又∵∠3=∠4(已知)
∴∠4+∠C=180º
∴ ∥ (同旁内角互补,两直线平行)
∴∠A=∠F( )